Liczba $\pi$ ukryta w liczbach pierwszych? Jak to możliwe? Przecież liczby pierwsze to „chaos”, a $\pi$ ma ścisły związek z najbardziej regularnym obiektem geometrycznym – tzn. z okręgiem / kołem.

Czym jest $\pi$?

• $\pi$ to stosunek obwodu koła do jego średnicy.
• $\pi$ to pole powierzchni koła o promieniu $1$.
• $\pi$ to połowa obwodu koła o promieniu $1$.
• $\pi$ to $\frac{1}{4}$ pola powierzchni sfery o promieniu $1$.
• $\pi$ to $\frac{3}{4}$ objętości kuli o promieniu $1$.
• $k\pi$ dla całkowitych $k$ to miejsca zerowe funkcji $\sin x$.
• … i wiele innych …

Czym są liczby pierwsze?

• Liczba pierwsza to liczba naturalna $n\in\mathbb{N}$ większa od $1$, której jednymi dzielnikami są $1$ oraz $n$.
• Liczby pierwsze to „atomy” w teorii liczb, tzn. każdą liczbę naturalną można rozłożyć na iloczyn liczb pierwszych.
• Rozmieszczenie liczb pierwszych wśród liczb naturalnych spełnia pewne zależności statystyczne, jednak nie jest znany żaden precyzyjny wzór dla określenia $n-tej$ liczby pierwszej. Ciekawskich odsyłam do artykułu „Prime-counting function”.

Czym są liczby względnie pierwsze?

• Dwie liczby $a,b\in\mathbb{N}$ nazywamy względnie pierwszymi jeśli ich największy wspólny dzielnik to $1$ – tzn. $NWD(a,b)=1$.
• Dwie liczby $a,b\in\mathbb{N}$ są względnie pierwsze wtedy i tylko wtedy, gdy obie nie mają wspólnego dzielnika będącego liczbą pierwszą.
• Liczby $a_1,a_2,\ldots,a_n$ są względnie pierwszy jeśli $NWD(a_1,a_2,\ldots,a_n)=1$.
• Zbiór liczb pierwszych to maksymalny „względnie pierwszy” podzbiór zbioru liczb naturalnych.

Czy dowolnie wybrane dwie liczby naturalne są względnie pierwsze?

Odpowiedź na to pytanie brzmi „nie” – bo mamy szereg takich kontrprzykładów jak: $\{3,6\}$, $\{8,2\}$. Musimy więc pytać jakie jest prawdopodobieństwo, że dowolnie wybrane dwie liczby naturalne są względnie pierwsze?

Zanim udzielę precyzyjnej odpowiedzi przeprowadzę symulację Monte Carlo z wykorzystaniem pakietu MathParser.org-mXparser.

Procedura symulacji:

• losujemy dwie liczby z liczb naturalnych – w mXparser „[Nat]” to zmienna losowa zwracająca losową liczbę naturalną;
• weryfikujemy czy największy wspólny dzielnik wylosowanych liczb to $1$ – korzystamy z funkcji „gcd” (greatest common divisor).
• zliczamy liczbę przypadków pozytywnych, powtarzamy $n$ razy, sumujemy wynik, dzielimy przez $n$.

Kod w mXparser dla 100, 10000, 1000000 powtórzeń:

/*
 * Definicja funkcji symulującej
 */
Function f = new Function("f(n) = sum(i, 1, n, gcd( [Nat], [Nat] ) = 1 )");

/*
 * Trzy warianty symulacji
 */
Expression e100 = new Expression("f(100) / 100", f);
Expression e10000 = new Expression("f(10000) / 10000", f);
Expression e1000000 = new Expression("f(1000000) / 1000000", f);

/*
 * Wyświetlenie wyniku
 */
mXparser.consolePrintln(e100.getExpressionString() + " = " + e100.calculate());
mXparser.consolePrintln(e10000.getExpressionString() + " = " + e10000.calculate());
mXparser.consolePrintln(e1000000.getExpressionString() + " = " + e1000000.calculate());

Wynik

[mXparser-v.4.1.1] f(100) / 100 = 0.55
[mXparser-v.4.1.1] f(10000) / 10000 = 0.6096
[mXparser-v.4.1.1] f(1000000) / 1000000 = 0.608361

Oszacowanie z Monte Carlo $P\approx 0.608361$

$$P\approx 0.608361\approx\frac{6}{10}$$

natomiast

$$\pi^2\approx 10$$

zatem

$$P\approx0.608361\approx\frac{6}{\pi^2}\approx 0.607927101854027$$

Czyżby prawdopodobieństwo, że dwie losowe liczby naturalne są względnie pierwsze wynosiło $\frac{6}{\pi^2}$?

$$P\Big(~NWD(a,b)=1~\Big|~a,b\in\mathbb{N}~\Big)=^\text{?}\frac{6}{\pi^2}$$

Pewien iloczyn Eulera

W 1734 roku Leonard Euler rozwiązał tzw. „Problem bazylejski”, jako pewien efekt uboczny powstała poniższa równość

$$\displaystyle\prod_{p-\text{l. pierwsza}}\Bigg(1-\frac{1}{p^2}\Bigg)=\frac{6}{\pi^2}$$

Nieskończony iloczyn na bazie liczb pierwszych powiązany jest z liczbą $\pi$ – zdumiewające! W dalszej części tekstu pokażę z czego to wynika, teraz skupię się na relacji powyższego iloczynu do naszego zagadnienia liczb względnie pierwszych i wyniku symulacji Monte Carlo.

Załóżmy, że $a,b\in\mathbb{N}$ zostały wybrane losowo, wtedy:

• prawdopodobieństwo, że $a$ jest parzysta wynosi $\frac{1}{2}$
• prawdopodobieństwo, że $b$ jest parzysta wynosi $\frac{1}{2}$
• prawdopodobieństwo, że $a$ i $b$ są jednocześnie parzyste wynosi $\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{2^2}$
• prawdopodobieństwo, że $a$ i $b$ jednocześnie nie są parzyste wynosi $1-\frac{1}{2^2}$

Analogicznie:

• prawdopodobieństwo, że $a$ jest podzielna przez $3$ wynosi $\frac{1}{3}$
• prawdopodobieństwo, że $b$ jest podzielna przez $3$ wynosi $\frac{1}{3}$
• prawdopodobieństwo, że $a$ i $b$ są jednocześnie podzielne przez $3$ wynosi $\frac{1}{3}\cdot\frac{1}{3}=\frac{1}{3^2}$
• prawdopodobieństwo, że $a$ i $b$ jednocześnie nie są podzielne przez $3$ wynosi $1-\frac{1}{3^2}$

Zatem prawdopodobieństwo, że $a$ i $b$ jednocześnie nie są podzielne przez $p$ wynosi $1-\frac{1}{p^2}$ dla dowolnej liczby $p$, w tym liczby pierwszej. Natomiast liczby $a$ i $b$ są względnie pierwsze wtedy i tylko wtedy, gdy obie nie mają wspólnego dzielnika będącego liczbą pierwszą. W ten sposób, jeśli udowodnimy niezależność zdarzeń (dzięki Olaf!), otrzymamy wzór na prawdopodobieństwo, że dwie losowo wybrane liczby naturalne są względnie pierwsze.

$$P\Big(~NWD(a,b)=1~\Big|~a,b\in\mathbb{N}~\Big)=\displaystyle\prod_{p-\text{l. pierwsza}}\Bigg(1-\frac{1}{p^2}\Bigg)=\frac{6}{\pi^2}$$

Niezależność zdarzeń

Zdarzenia $A$ i $B$ są niezależne jeśli wiedza o zdarzeniu $A$ nie wpływa na prawdopodobieństwo zdarzenia $B$ i odwrotnie, co zapisujemy

$P(B|A)=P(B)$ oraz $P(A|B)=P(A)$

$$P(A\cap B)=P(A)\cdot P(B)$$

Załóżmy, że $n,m\in\mathbb{N}$ zostały wybrane losowo.

Spostrzeżenie: jeśli ustalone $a,b\in\mathbb{N}$ są względnie pierwsze to niezależne są zdarzenia:

• $a$ jest dzielnikiem $n$
• $b$ jest dzielnikiem $n$

Uzasadnienie:

• $P(a\text{ dzieli }n )=\frac{1}{a}$
• $P(b\text{ dzieli }n)=\frac{1}{b}$
• $P(a\cdot b\text{ dzieli }n)=\frac{1}{ab}=P(a\text{ dzieli }n )\cdot P(b\text{ dzieli }n )$
• $P(a \text{ i } b\text{ dzieli }n)=\text{?}$

$a$ i $b$ są względnie pierwsze, więc $n$ jest podzielne przez $a$ i $b$ wtedy i tylko wtedy gdy jest podzielne przez $ab$. Zatem

$$P(a \text{ i } b\text{ dzieli }n)=\frac{1}{ab}=P(a\text{ dzieli }n )\cdot P(b\text{ dzieli }n )$$

Spostrzeżenie: jeśli ustalone $a,b\in\mathbb{N}$ są względnie pierwsze to niezależne są zdarzenia:

• $a$ jest dzielnikiem $n$ oraz $m$
• $b$ jest dzielnikiem $n$ oraz $m$

Uzasadnienia dokonujemy analogicznie.

Spostrzeżenie: jeśli $\{p_1,p_2,\ldots,p_n\}$ są ustalonymi liczbami pierwszymi to niezależne są zdarzenia, że $p_i$ dzieli jednocześnie $n$ i $m$.

Spostrzeżenie: jeśli $p$ i $q$ są ustalonymi liczbami pierwszymi to niezależne są zdarzenia, że:

• $p$ nie dzieli jednocześnie $n$ i $m$
• $q$ nie dzieli jednocześnie $n$ i $m$

Spostrzeżenie: jeśli $\{p_1,p_2,\ldots,p_n\}$ są ustalonymi liczbami pierwszymi to niezależne są zdarzenia, że $p_i$ nie dzieli jednocześnie $n$ i $m$.

Po więcej szczegółów odsyłam do pracy „Some Early Analytic Number Theory”.

Relacja iloczynu Eulera do problemu bazylejskiego

Przedmiotem problemu bazylejskiego, w jego pierwotnym brzmieniu, było znalezienie sumy odwrotności kwadratów wszystkich liczb naturalnych, tj. sumy szeregu:

$$\displaystyle\sum_{n=1}^\infty\frac{1}{n^2}=\text{?}$$

Zdefiniujmy zagadnienie bardziej ogólnie

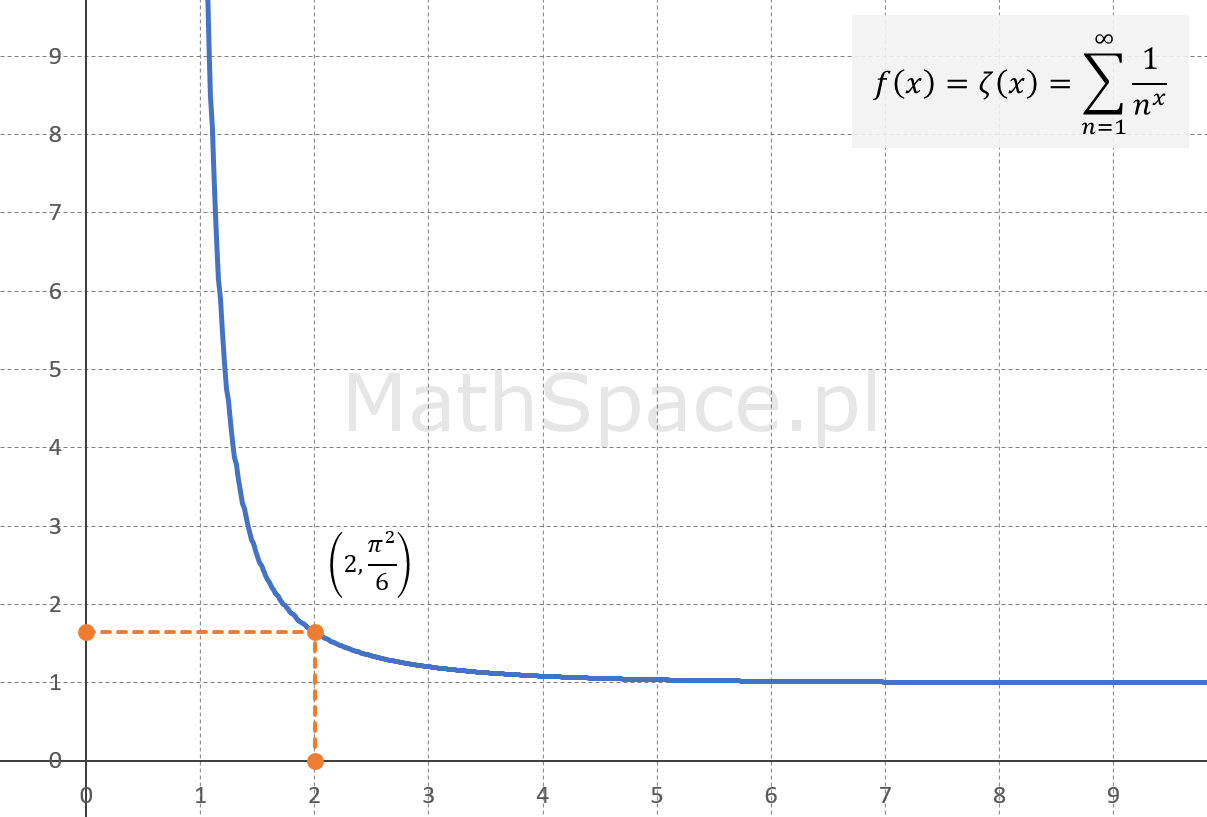
$$\zeta(s)=\displaystyle\sum_{n=1}^\infty\frac{1}{n^s}=\text{?}$$

dla $s>1$

$$\zeta(s)=1+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\frac{1}{5^s}+\ldots$$

Mnożymy obie strony przez $\frac{1}{2^s}$

$$\frac{1}{2^s}\zeta(s)=\frac{1}{2^s}+\frac{1}{2^s2^s}+\frac{1}{2^s3^s}+\frac{1}{2^s4^s}+\frac{1}{2^s5^s}+\ldots$$

$$\zeta(s)=1+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\frac{1}{5^s}+\ldots$$

Odejmujemy

$$\zeta(s)-\frac{1}{2^s}\zeta(s)=\Big(1-\frac{1}{2^s}\Big)\zeta(s)$$

---

$$\zeta(s)=1+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\frac{1}{5^s}+\ldots$$

$$\frac{1}{2^s}\zeta(s)=\frac{1}{2^s}+\frac{1}{4^s}+\frac{1}{6^s}+\frac{1}{8^s}+\frac{1}{10^s}+\ldots$$

---

$$\Big(1-\frac{1}{2^s}\Big)\zeta(s)=1+\frac{1}{3^s}+\frac{1}{5^s}+\frac{1}{7^s}+\frac{1}{9^s}+\frac{1}{11^s}+\ldots$$

Po odjęciu pozostały tylko te składniki $\frac{1}{n^s}$, dla których $n$ nie jest podzielne przez $2$.

Mnożymy obie strony przez $\frac{1}{3^s}$

$$\frac{1}{3^s}\Big(1-\frac{1}{2^s}\Big)\zeta(s)=\frac{1}{3^s}+\frac{1}{3^s3^s}+\frac{1}{3^s5^s}+\frac{1}{3^s7^s}+\frac{1}{3^s9^s}+\frac{1}{3^s11^s}+\ldots$$

$$\frac{1}{3^s}\Big(1-\frac{1}{2^s}\Big)\zeta(s)=\frac{1}{3^s}+\frac{1}{9^s}+\frac{1}{15^s}+\frac{1}{21^s}+\frac{1}{27^s}+\frac{1}{33^s}+\ldots$$

Odejmujemy

$$\Big(1-\frac{1}{2^s}\Big)\zeta(s)-\frac{1}{3^s}\Big(1-\frac{1}{2^s}\Big)\zeta(s)=\Big(1-\frac{1}{3^s}\Big)\Big(1-\frac{1}{2^s}\Big)\zeta(s)$$

---

$$\Big(1-\frac{1}{2^s}\Big)\zeta(s)=1+\frac{1}{3^s}+\frac{1}{5^s}+\frac{1}{7^s}+\frac{1}{9^s}+\frac{1}{11^s}+\ldots$$

$$\frac{1}{3^s}\Big(1-\frac{1}{2^s}\Big)\zeta(s)=\frac{1}{3^s}+\frac{1}{9^s}+\frac{1}{15^s}+\frac{1}{21^s}+\frac{1}{27^s}+\frac{1}{33^s}+\ldots$$

---

$$\Big(1-\frac{1}{3^s}\Big)\Big(1-\frac{1}{2^s}\Big)\zeta(s)=1+\frac{1}{5^s}+\frac{1}{7^s}+\frac{1}{11^s}+\frac{1}{13^s}+\frac{1}{17^s}+\ldots$$

Po odjęciu pozostały tylko te składniki $\frac{1}{n^s}$, dla których $n$ nie jest podzielne przez $2$ lub przez $3$. Widać działanie swego rodzaju „sita”.

Powtarzamy mnożenie przez $\frac{1}{p^s}$ (i odejmowanie) dla wszystkich liczb pierwszych $p$.

W ten sposób prawa strona równania jest „przesiewana” przez kolejne „dzielniki”, gdzie w nieskończonym kroku pozostaje tylko liczba 1.

$$\ldots \Big(1-\frac{1}{11^s}\Big)\Big(1-\frac{1}{7^s}\Big)\Big(1-\frac{1}{5^s}\Big)\Big(1-\frac{1}{3^s}\Big)\Big(1-\frac{1}{2^s}\Big)\zeta(s)=1$$

$$\zeta(s)\displaystyle\prod_{p-\text{l. pierwsza}}\Bigg(1-\frac{1}{p^s}\Bigg)=1$$

$${\Large\zeta(s)}=\frac{{\Large 1}}{\displaystyle\prod_{p-\text{l. pierwsza}}\Bigg(1-\frac{1}{p^s}\Bigg)}$$

$$\zeta(s)=\displaystyle\prod_{p-\text{l. pierwsza}}\Bigg(1-\frac{1}{p^s}\Bigg)^{-1}$$

Ostatecznie

$$P\Big(~NWD(a,b)=1~\Big|~a,b\in\mathbb{N}~\Big)={\large\frac{1}{\zeta(2)}}$$

Funkcja $\zeta(s)$ nazywana jest funkcją dzeta Riemanna – tak tak, to ta funkcja od słynnej hipotezy Riemanna 🙂

Jak Euler wyznaczył wartość funkcji $\zeta(2)$?

Euler badał funkcję $\frac{\sin x}{x}$, a dokładnie jej rozwinięcie w szereg Taylora.

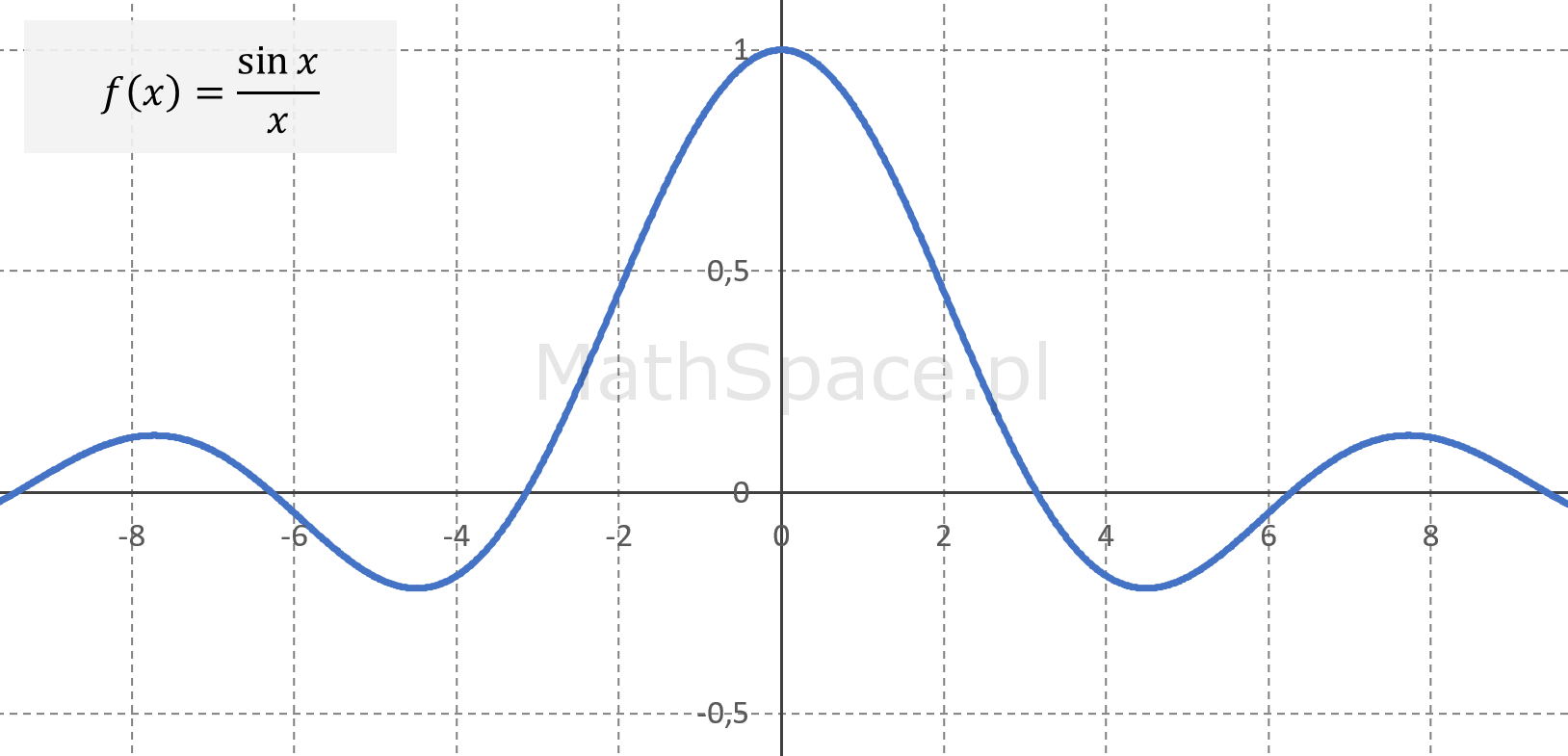
$\frac{\sin x}{x}$ w $x=0$ nie ma wartości, ale posiada granicę $\lim_{x\to 0}\frac{\sin x}{x}=1$ – wartość granicy wyznaczyłem tutaj.

Rozważmy rozwinięcie funkcji $\sin x$ w szereg Maclaurina

$$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}\ldots=\displaystyle\sum_{n=0}^\infty(-1)^n\frac{x^{2n+1}}{(2n+1)!}$$

Dzieląc przez $x$ otrzymujemy

$$f(x)=\frac{\sin x}{x}=1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}\ldots=\displaystyle\sum_{n=0}^\infty(-1)^n\frac{x^{2n}}{(2n+1)!}$$

W tej reprezentacji $f(0)=1$, łatwo też zauważyć, że $f(x)=f(-x)$. Z własności funkcji $\sin x$ wnioskujemy, że $f(x)$ ma miejsca zerowe postaci $x=\pm k\pi$ dla $k=1,2,3,\ldots$.

Postać iloczynowa wielomianu

Postać iloczynowa wielomianu stopnia $n$ posiadającego $n$ pierwiastków jednokrotnych $x_1,x_2,\ldots,x_n$ to

$$a(x-x_1)(x-x_2)\ldots(x-x_n)$$

$a$ – pewna stała

 Powyższe można zapisać równoważnie

$$a(-x_1)\Big(1-\frac{x}{x_1}\Big)(-x_2)\Big(1-\frac{x}{x_2}\Big)\ldots(-x_n)\Big(1-\frac{x}{x_n}\Big)$$

$$A\Big(1-\frac{x}{x_1}\Big)\Big(1-\frac{x}{x_2}\Big)\ldots\Big(1-\frac{x}{x_n}\Big)$$

$A$ – pewna stała

Postać iloczynowa wielomianu funkcji $f(x)=\frac{\sin x}{x}$

Rozwinięcie w „nieskończony” wielomian Taylora oraz symetryczne miejsca zerowe (jednokrotne) sugerują, że $f(x)$ można przedstawić w nieskończonej postaci iloczynowej.

$$f(x)=A\Big(1-\frac{x}{\pi}\Big)\Big(1+\frac{x}{\pi}\Big)\Big(1-\frac{x}{2\pi}\Big)\Big(1+\frac{x}{2\pi}\Big)\ldots\Big(1-\frac{x}{k\pi}\Big)\Big(1+\frac{x}{k\pi}\Big)\ldots$$

$$f(x)=A\displaystyle\prod_{k=1}^\infty\Big(1-\frac{x}{k\pi}\Big)\Big(1+\frac{x}{k\pi}\Big)$$

$$f(x)=A\displaystyle\prod_{k=1}^\infty\Bigg(1-\Big(\frac{x}{k\pi}\Big)^2\Bigg)$$

W rozwinięciu Taylora $f(0)=1$

$$f(0)=A=1$$

ostatecznie

$$f(x)=\displaystyle\prod_{k=1}^\infty\Bigg(1-\Big(\frac{x}{k\pi}\Big)^2\Bigg)$$

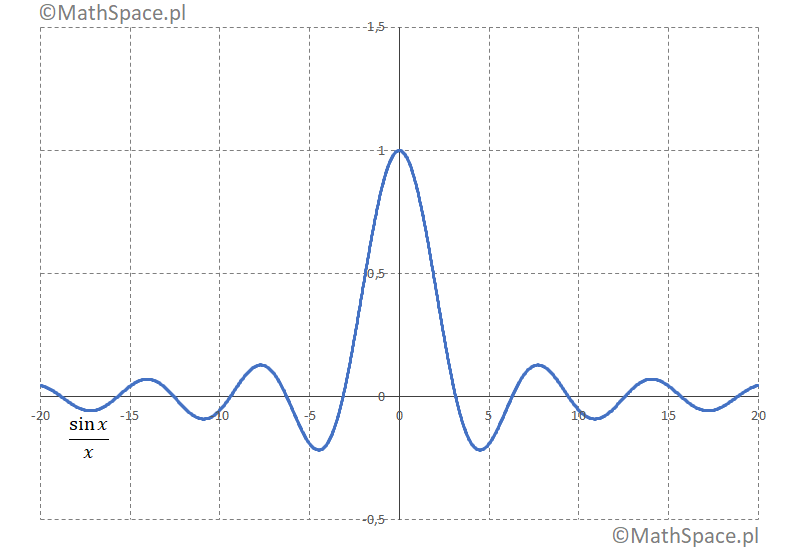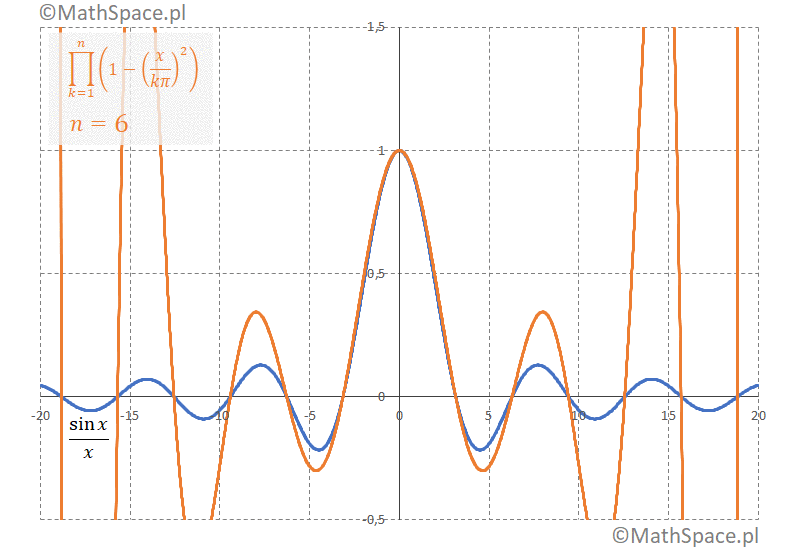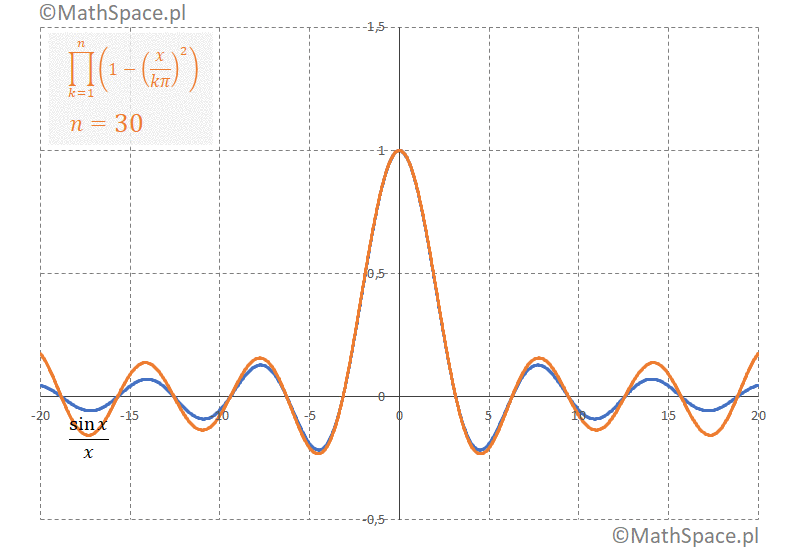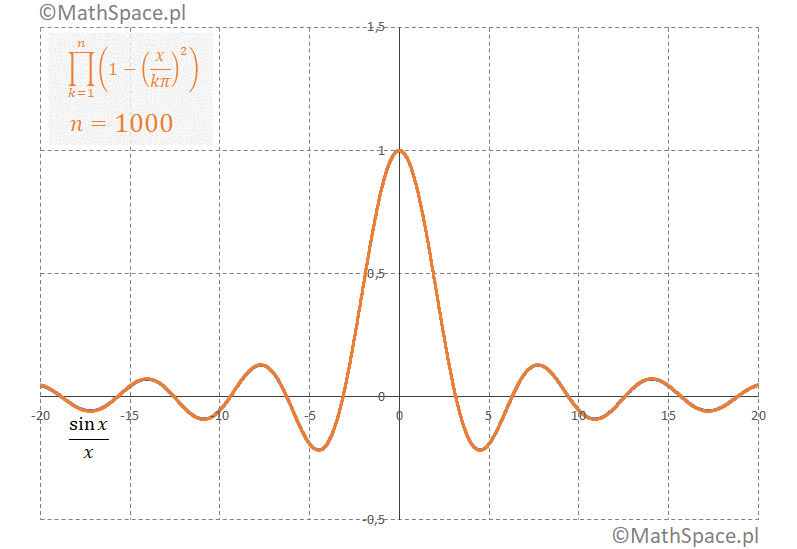
Porównanie wielomianu Taylora z postacią iloczynową

Rozwiązanie problemu bazylejskiego ujawnia się po porównaniu nieskończonego wielomianu Taylora z rozwinięcia funkcji $\frac{\sin x}{x}$ z jego postacią iloczynową

$$\displaystyle\sum_{n=0}^\infty(-1)^n\frac{x^{2n}}{(2n+1)!}=\displaystyle\prod_{k=1}^\infty\Bigg(1-\Big(\frac{x}{k\pi}\Big)^2\Bigg)$$

Po prawej stronie równania przeprowadzamy „nieskończone” mnożenie „każdy z każdym”, w kolejnym kroku szeregując elementy w grupy $x^2$, $x^4$, $x^6$, $\ldots$. Zauważmy (między innymi), że:

• „1” mnoży się ze wszystkimi jedynkami – zatem wyraz wolny to 1. Każde inne mnożenie „kontrybuuje” do potęg $x^{2k}$, gdzie $k\geq 1$;
• element $\frac{x^2}{\pi}$ mnoży się z pozostałymi jedynkami, co daje jasną postać współczynnika przy $x^2$. Każde inne mnożenie „kontrybuuje” do potęg $x^{2k}$, gdzie $k\geq 2$.

$$1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}\ldots=1-x^2\Big(\frac{1}{2^2\pi^2}+\frac{1}{3^2\pi^2}+\frac{1}{4^2\pi^2}+\ldots\Big)+x^4\Big(\ldots\Big)+\ldots$$

Porównując współczynniki przy $x^2$

$$-\frac{x^2}{3!}=-x^2\Big(\frac{1}{2^2\pi^2}+\frac{1}{3^2\pi^2}+\frac{1}{4^2\pi^2}+\ldots\Big)$$

$$\frac{x^2}{3!}=\frac{x^2}{\pi^2}\displaystyle\sum_{n=1}^\infty\frac{1}{n^2}$$

$$\frac{\pi^2}{3!}=\displaystyle\sum_{n=1}^\infty\frac{1}{n^2}$$

$$\displaystyle\sum_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6}=\zeta(2)$$

Finalnie

$$P\Big(~NWD(a,b)=1~\Big|~a,b\in\mathbb{N}~\Big)={\large\frac{1}{\zeta(2)}}=\frac{6}{\pi^2}$$

Niedostateczna precyzja dowodu Eulera

Rozwijając funkcję $f(x)=\frac{\sin x}{x}$ w produkt $f(x)=\displaystyle\prod_{k=1}^\infty\Bigg(1-\Big(\frac{x}{k\pi}\Big)^2\Bigg)$ otrzymaliśmy zgodność wszystkich miejsc zerowych oraz zgodność wartości w punkcie $x=0$. To jednak nie gwarantuje równości obu funkcji – np.  $e^x\frac{\sin x}{x}$ to inna funkcja. Euler rozumiał niekompletność swojego wywodu, jednak nie potrafił dostatecznie uściślić wyniku. Jego intuicja okazała się słuszna i potwierdzona w twierdzeniu Weierstrass o faktoryzacji. Zainteresowanych odsyłam do publikacji „Weierstrass factorization theorem”.

Oszacowanie $\pi$ na bazie symulacji Monte Carlo

Dla 1000000 eksperymentów, polegających na wylosowaniu dwóch liczb naturalnych i weryfikacji czy są względnie pierwsze, otrzymaliśmy

$$P\approx 0.608361$$

Co daje oszacowanie $\pi$ z dokładnością jedynie do 2 miejsc „po przecinku”

$$\pi\approx\sqrt{\frac{6}{0.608361}}\approx 3.140472123$$

Podsumowanie

Dzisiejszy wpis to bardzo dużo „znaczków”, mglistych przejść, ciągła praca z nieskończonymi szeregami i produktami – ale takie były właśnie dowody Eulera 🙂 Gratuluję wszystkim, którzy „dotrwali” do końca, materiał nie był łatwy, ale za to bardzo treściwy. Pomiędzy liczbami pierwszymi (czyli najmniejszymi częściami składowymi teorii liczb) a liczbą $\pi$, istnieje zaskakujący związek, dużo głębszy niż tylko symbol współdzielony z „funkcją zliczającą liczby pierwsze” $\pi(n)$ – po szczegóły odsyłam do artykułu „Prime-counting function”.

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

https://youtu.be/YSOZPiXw6CY

https://youtu.be/XTOjmucEAsw

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa