Dziś ciekawostka w nawiązaniu do wpisu z dnia 20 października 2015 roku „Liczba PI ukryta w zbiorze Mandelbrota”, ujawniająca nietrywialne powiązanie liczby $\pi$ z prędkością ucieczki do nieskończoności przy zbliżaniu się punktu startu iteracji do „ostrza” zbioru Mandelbrota. Brzmi trochę skomplikowanie? Poniżej wyjaśnienie 🙂

Zbliżanie się do „ostrza” zbioru Mandelbrota

Rozważmy równanie rekurencyjne dla liczb rzeczywistych

$$x_n=\begin{cases}x_{n-1}^2+\frac{1}{4}+\epsilon&\text{dla}\quad n>0\\0&\text{dla}\quad n=0\end{cases}$$

Powyższe wyrażenie powstaje na bazie równania (w liczbach zespolonych) opisującego zbiór Mandelbrota

$$z_n=z_{n-1}^2+c$$

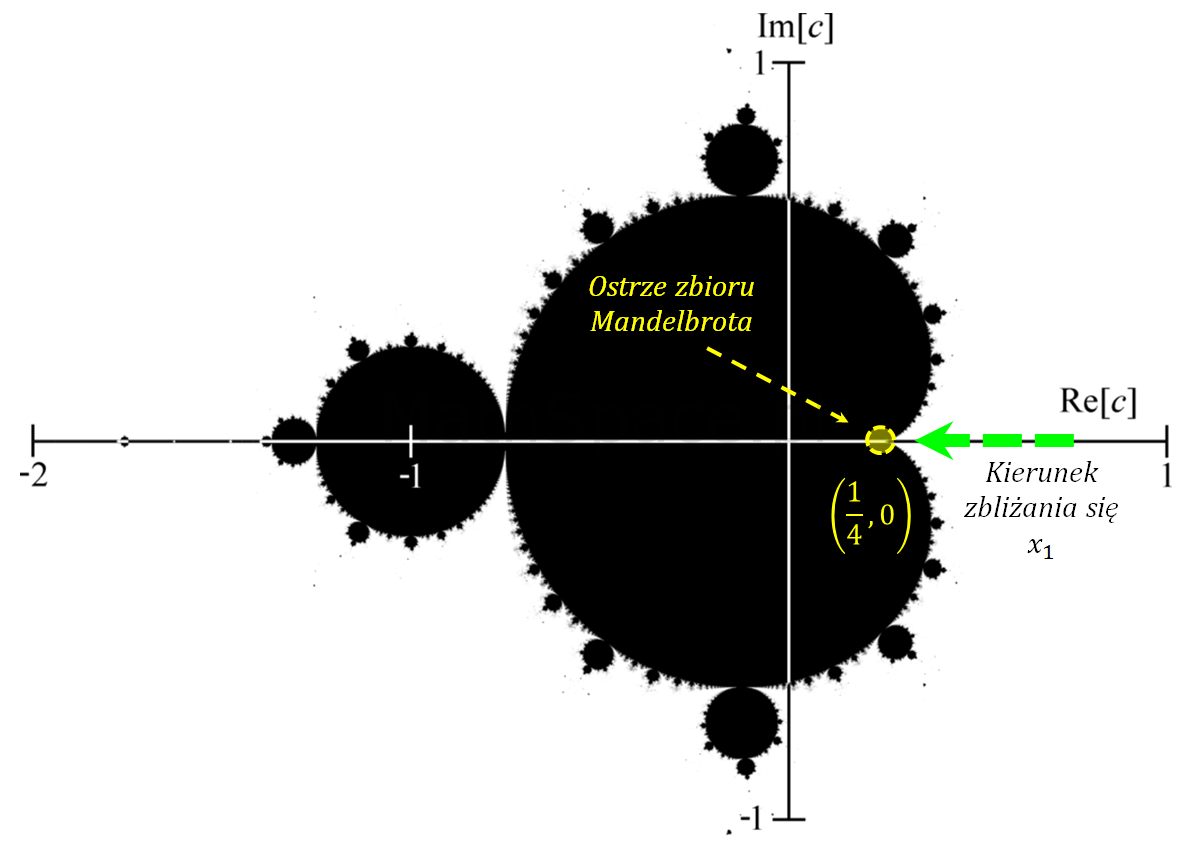
Ograniczając się do prostej rzeczywistej (dlatego użyłem zapisu $x_n$) przeanalizujmy zachowanie $x_n$ przy zbliżaniu się elementu $x_1=\frac{1}{4}+\epsilon$ do „ostrza” (ang. „cusp”) zbioru – ostrze to punkt o współrzędnych $(\frac{1}{4},0)$.

Szybkość ucieczki do nieskończoności

Ustalając odpowiednio małe $\epsilon>0$ decydujemy jak bardzo chcemy się zbliżyć do „ostrza”. Teraz zadanie polega na znalezieniu pierwszego $n$, dla którego $x_n>=2$. Takie minimalne $n$ jest dobrą miarą prędkości ucieczki $x_n$ do nieskończoności w zależności od wybranego $\epsilon$. Na marginesie dodam, że zbiór Juli dla równania Mandelbrota (na powyższym obrazku oznaczony kolorem czarnym), reprezentuje punkty „nieuciekające” do nieskończoności w trakcie nieskończonej iteracji . Ta tematyka jest sama w sobie bardzo ciekawa i zapewne kiedyś coś napiszę o atraktorach.

$$x_n=\begin{cases}x_{n-1}^2+\frac{1}{4}+\epsilon&\text{dla}\quad n>0\\0&\text{dla}\quad n=0\end{cases}$$

$$N_\epsilon=\min\big\{n~|~x_n\ge2\big\}$$

Rekurencja na rekurencji

W celu poszukiwania rozwiązania zapisujemy zadanie wykorzystując rekurencję

$$N(n,\epsilon)=\begin{cases}N(n+1,\epsilon)&\text{dla}\quad x_n<2\\n&\text{dla}\quad x_n>=2\end{cases}$$

Nietrudno zauważyć, że zdefiniowaliśmy rekurencję na rekurencji. To zły znak dla wydajności.

Test w MathParser.org-mXparser

/* Definicja funkcji rekurencyjnej */
Function x = new Function("x(n, eps) = if( n > 0, x(n-1, eps)^2 + 0.25 + eps, 0 )");
Function N = new Function("N(n, eps) = if( x(n, eps) >= 2, n, N(n+1, eps) )", x);

/* Obliczenia i wyświetlenie wyniku */
mXparser.consolePrintln( "eps = 0.01" + ", N(0, eps) = " + N.calculate(0, 0.01) + ", czas = " + N.getComputingTime() + " s" );
mXparser.consolePrintln( "eps = 0.0001" + ", N(0, eps) = " + N.calculate(0, 0.0001) + ", czas = " + N.getComputingTime() + " s" );
mXparser.consolePrintln( "eps = 0.000001" + ", N(0, eps) = " + N.calculate(0, 0.000001) + ", czas = " + N.getComputingTime() + " s" );
mXparser.consolePrintln( "eps = 0.00000001" + ", N(0, eps) = " + N.calculate(0, 0.00000001) + ", czas = " + N.getComputingTime() + " s" );

+ wyczekiwany wynik

eps = 0.01, N(0, eps) = 30.0, czas = 0.224 s
eps = 0.0001, N(0, eps) = 312.0, czas = 1.532 s
eps = 0.000001, N(0, eps) = 3140.0, czas = 37.343 s
eps = 0.00000001, N(0, eps) = 31414.0, czas = 4068.338 s

Wzorzec prędkości ucieczki

$$\epsilon=\frac{1}{10}\Rightarrow N_\epsilon=30$$

$$\epsilon=\frac{1}{1000}\Rightarrow N_\epsilon=312$$

$$\epsilon=\frac{1}{100000}\Rightarrow N_\epsilon=3140$$

$$\epsilon=\frac{1}{10000000}\Rightarrow N_\epsilon=31414$$

…

WOW! Jaki super wzorzec liczby wymaganych iteracji, aby przekroczyć 2! Dostajemy coś, co przypomina $\pi$, jednak wymaga postawienia „przecinka” w odpowiednim miejscu! Można również zauważyć, że 100-krotne zmniejszenie $\epsilon$ zwiększa niezbędną liczbę iteracji około 10-krotnie. Zmniejszając $\epsilon$ otrzymujemy liczbę coraz bardziej „przypominającą” $\pi$ 🙂

Pozdrowienia,

Mariusz Gromada

Zobacz również:

1. Polowanie na czarownice – czyli zabawy z rekurencją (część 1)
2. Naiwny test pierwszości – czyli zabawy z rekurencją (część 3)
3. Rekurencja pośrednia – czyli zabawy z rekurencją (część 4)
4. Liczba PI ukryta w zbiorze Mandelbrota

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa