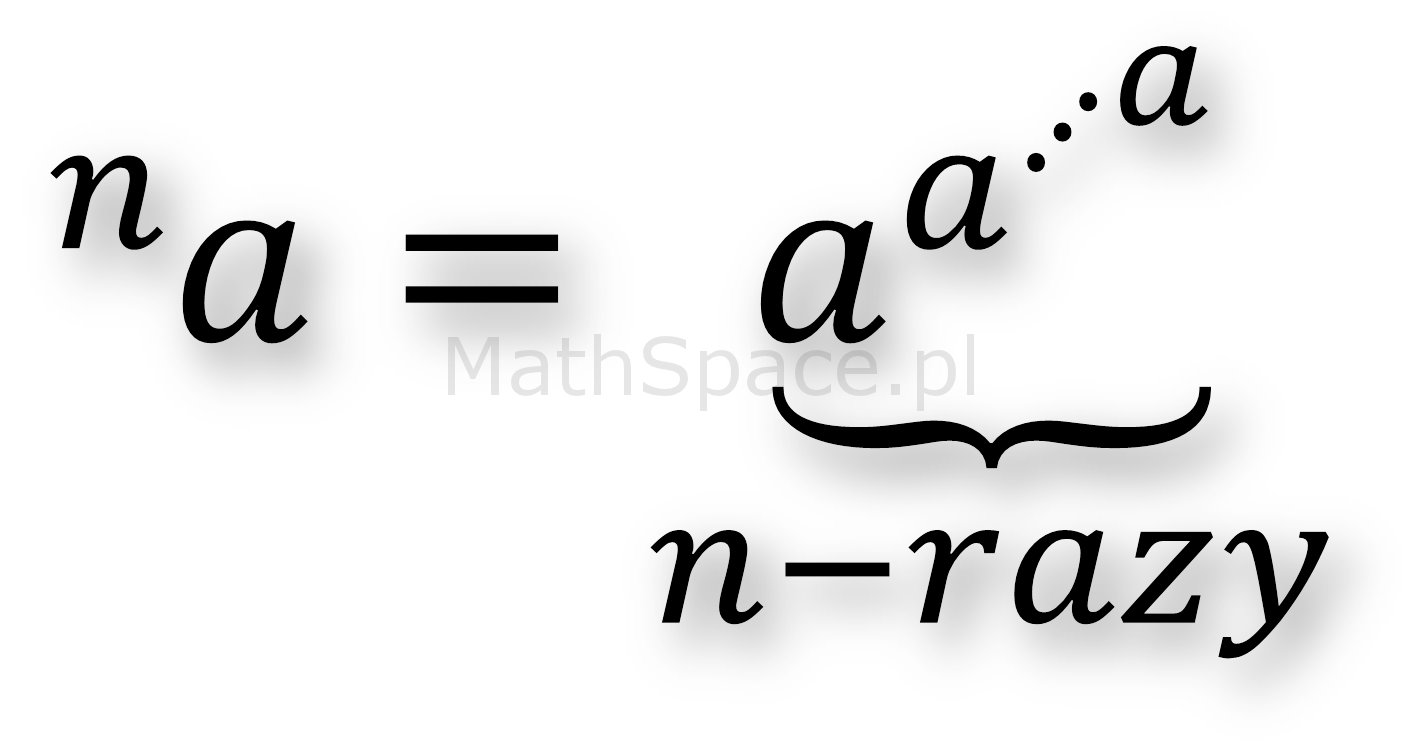
Tetracja (wieża wykładnicza, super-potęgowanie, iterowane potęgowanie, 4 hiper-operator)
Tetracja to działanie dwuargumentowe definiowane jako wielokrotne potęgowanie elementu przez siebie.
Definicja: dla dowolnej liczby rzeczywistej $a>0$ i nieujemnej liczby całkowitej $n\geq 0$ tetrację $n$ liczby $a$ definiujemy jako:
$${^{n}a}=\begin{cases}1&\text{dla}\quad n=0\\a&\text{dla}\quad n=1\\ \underbrace{a^{a^{\cdots^{a}}}}_{n}&\text{dla}\quad n>1\end{cases}$$
Przykłady
$${^{3}2}=2^{2^2}=2^{(2^2)}=2^4=16$$
$${^{4}2}=2^{2^{2^2}}=2^{(2^{(2^2)})}=2^{(2^{4})}=2^{16}=65536$$
$${^{3}3}=3^{3^3}=3^{(3^3)}=3^{27}=7625597484987$$
$${^{4}3}=3^{3^{3^3}}=3^{(3^{(3^3)})}=3^{(3^{27})}=3^{7625597484987}=\ldots$$ liczba składająca się z $$3638334640025$$ cyfr 🙂
Tetrację można wykorzystać do zapisu naprawdę dużych liczb, co dobrze obrazuje przykład ${^{4}3}$. Tetrację wygodnie jest również definiować w postaci rekurencyjnej.
Definicja rekurencyjna: dla dowolnej liczby rzeczywistej $a>0$ i nieujemnej liczby całkowitej $n\geq 0$ tetrację $n$ liczby $a$ definiujemy jako:
$${^{n}a}=\begin{cases}1&\text{dla}\quad n=0\\a^{{^{n-1}a}}&\text{dla}\quad n\geq 1\end{cases}$$