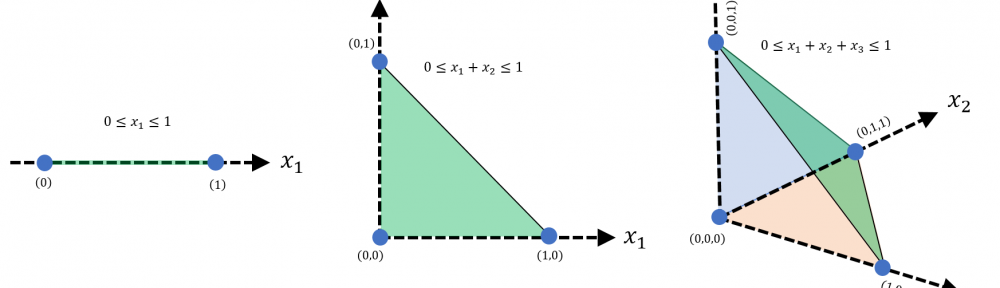
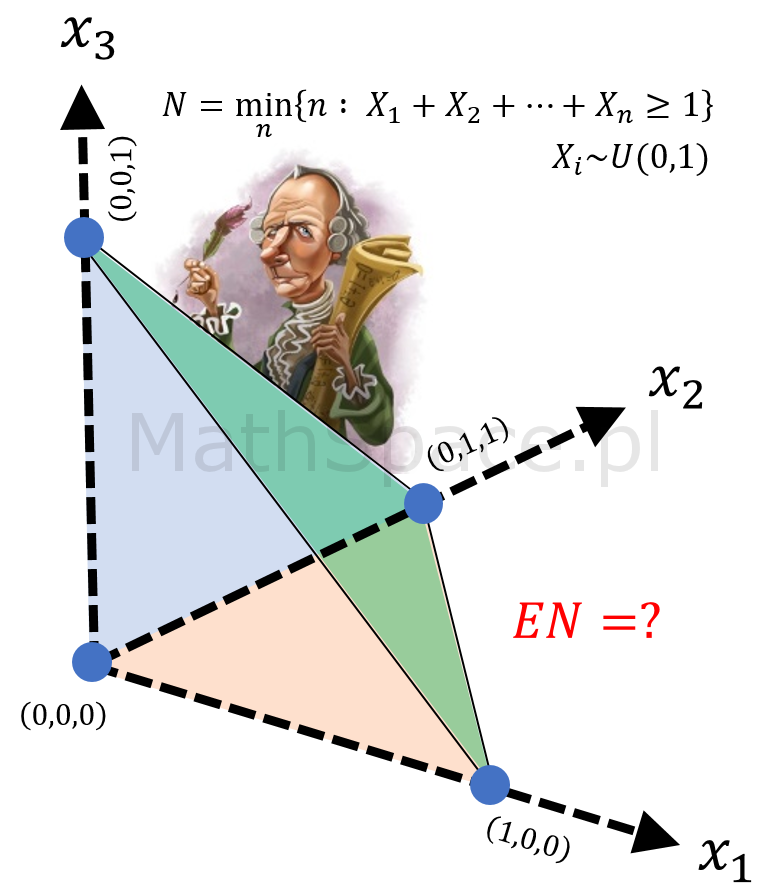
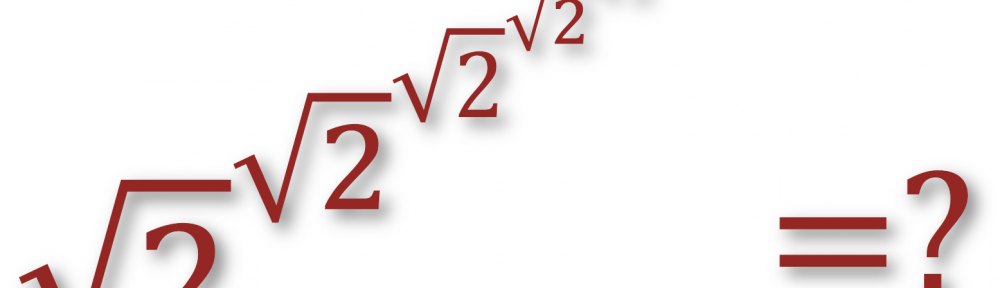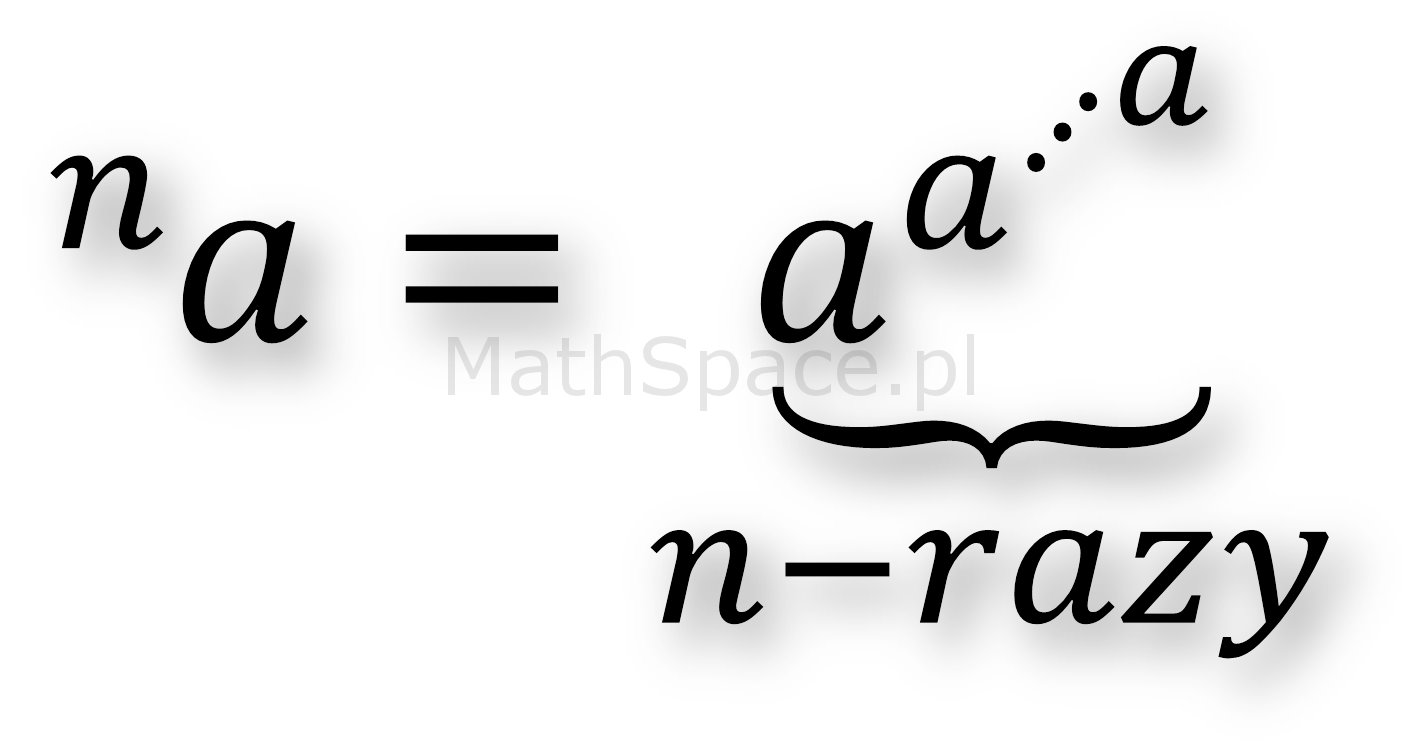by ·0 Comments

Funkcja e do x (e^x)

„Plaża, piękna pogoda, sielanka i relaks! Różne funkcje wypoczywają. Nagle … popłoch, panika! Funkcje uciekają. Tylko jedna nadal się opala.

– Co robisz? Uciekaj! Nadchodzi operator różniczkowy!

– Nie boję się, jestem $e^x$. 

I tak spokojna $e^x$ została. Wpada operator.

– Wrrr! Teraz Cię zróżniczkuję! Wrrr!

– A proszę bardzo – jestem $e^x$ – nic mi nie grozi.

– Kochana, ja różniczkuję po $dy$”

Ten iście „nerdowski” dowcip całkiem dobrze rozpoczyna kolejną część serii „o liczbie e”. Na bazie pochodnej przedstawię dodatkowe argumenty „dlaczego?” liczba e jest tak naturalna. Zaczynamy od powtórki podstaw w zakresie potęgowania. Prawdopodobnie zaskoczę Cię już samą definicją funkcji wykładniczej $a^x$ 🙂

Definicja funkcji wykładniczej na bazie potęgowania

Continue reading

by ·2 komentarze

Liczba e

Funkcja wykładnicza i logarytm wprowadzane są w szkole średniej (przynajmniej tak było w moim przypadku). Zazwyczaj wtedy poznajemy liczbę $e$, którą magicznie nazywa się podstawą logarytmu naturalnego.

$$e\approx 2.718\ldots$$

Nazwa dobrana jest świetnie, niestety nikt nie tłumaczy dlaczego tak właściwie jest. Cała sprawa jest niezwykle ciekawa, jej wyjaśnienie to temat nowej serii artykułów „o liczbie e”. Tym samym wzbogacam cykl „dlaczego?”. Dowody przeprowadzę „metodą elementarną” – wszak chodzi o „pierwotność / naturalność” $e$. Będzie kilka dużych „odcinków” – zapraszam 🙂

Nota historyczna

Liczba e pojawia się w wielu dziedzinach. W matematyce jest wszechobecna! Z powodzeniem dorównuje liczbie $\pi$. Analiza matematyczna (w szczególności rachunek różniczkowy i całkowy, równania różniczkowe), funkcje specjalne, analiza zespolona, rachunek prawdopodobieństwa, statystyka matematyczna – to najbardziej wyraziste przykłady. W innych naukach ścisłych (np.: ekonomia, fizyka, biologia) liczba e pojawia się w wielu ważnych równaniach, w tym: równanie przewodnictwa cieplnego, wzór barometryczny, rozpady promieniotwórcze, fazory, funkcja falowa w mechanice kwantowej, wzrost populacji, procent składany.

Pierwsze informacje na temat liczby e pojawiły się w 1618 roku. Opublikował je John Napier, przygotowując tabele logarytmów. Praca nie zawierała samej stałej, prezentowała niektóre wartości logarytmów na bazie e. Liczbę e w jej dzisiejszej postaci odkrył Jacob Bernoulli. Dokonał tego w 1683 roku analizując własności procentu składanego. Pierwsze udokumentowane wykorzystanie liczby e, wtedy oznaczanej przez b, pojawiło się w latach 1690-1691 (Gottfried Leibniz, Christiaan Huygens). Wykorzystanie stałej znacząco rozwinął Leonhard Euler oznaczając ją w 1727 roku do dziś wykorzystywanym symbolem $e$.

Procent składany

Continue reading

by ·0 Comments
1, 2, 3 - sympleks

Rozkład jednostajny na odcinku $(0,1)$, chyba najprostszy z możliwych rozkładów ciągłych, z pozoru niezbyt interesujący, a jednak 🙂 Dziś ciekawostka wiążąca rozkład sumy rozkładów jednostajnych z liczbą Eulera e.

Uniform Sum Distribution

Rozkład jednostajny ciągły na odcinku (a,b)

Rozkład jednostajny ciągły na odcinku $(a,b)$ jest opisany poniższą funkcją gęstości.

$$f(x)=\begin{cases}\frac{1}{b-a}&&\text{dla }a\leq x\leq b\\0&&\text{w p.p.}\end{cases}$$

Pisząc $X\sim U(a,b)$ oznaczamy, że zmienna losowa $X$ ma rozkład jednostajny ciągły na odcinku $(a,b)$. Jest to rozkład ciągły, zatem przyjęcie wartości $0$ lub $\frac{1}{b-a}$ w punktach $x=a$ i $x=b$ jest umowne i nie ma zwykle wpływu na własności i rozważania.

Continue reading

by ·4 komentarze
Nieskończone potęgowanie

Tetracja - definicja

Tetracja (wieża wykładnicza, super-potęgowanie, iterowane potęgowanie, 4 hiper-operator)

Tetracja to działanie dwuargumentowe definiowane jako wielokrotne potęgowanie elementu przez siebie.

Definicja: dla dowolnej liczby rzeczywistej $a>0$ i nieujemnej liczby całkowitej $n\geq 0$ tetrację $n$ liczby $a$ definiujemy jako:

$${^{n}a}=\begin{cases}1&\text{dla}\quad n=0\\a&\text{dla}\quad n=1\\ \underbrace{a^{a^{\cdots^{a}}}}_{n}&\text{dla}\quad n>1\end{cases}$$

Przykłady

$${^{3}2}=2^{2^2}=2^{(2^2)}=2^4=16$$

$${^{4}2}=2^{2^{2^2}}=2^{(2^{(2^2)})}=2^{(2^{4})}=2^{16}=65536$$

$${^{3}3}=3^{3^3}=3^{(3^3)}=3^{27}=7625597484987$$

$${^{4}3}=3^{3^{3^3}}=3^{(3^{(3^3)})}=3^{(3^{27})}=3^{7625597484987}=\ldots$$ liczba składająca się z $$3638334640025$$ cyfr 🙂

Tetrację można wykorzystać do zapisu naprawdę dużych liczb, co dobrze obrazuje przykład ${^{4}3}$. Tetrację wygodnie jest również definiować w postaci rekurencyjnej.

Definicja rekurencyjna: dla dowolnej liczby rzeczywistej $a>0$ i nieujemnej liczby całkowitej $n\geq 0$ tetrację $n$ liczby $a$ definiujemy jako:

$${^{n}a}=\begin{cases}1&\text{dla}\quad n=0\\a^{{^{n-1}a}}&\text{dla}\quad n\geq 1\end{cases}$$

Continue reading