Osiągnięcia matematyczne są tym większe im bardziej uogólnione rezultaty są przedstawiane. Teorie matematyczne zawsze dążą do systematyzowania i generalizowania pojęć, umożliwiając ich aplikację w znacznie szerszej klasie problemów. Przykładowo matematyk nie zgłosi trudności z wyobrażeniem sobie 4 wymiarów, zwyczajnie analizuje n-wymiarów i podstawia n = 4 🙂 .
Teoria miary i całki
Jednym z ciekawszych przejawów tego trendu jest teoria miary i całki, która wyrosła z potrzeby ujednolicenia pod pojęciem rozmiaru zbioru jego długości, pola powierzchni, czy też objętości. Nową dziedzinę matematyki zaproponował na początku XX wieku Henri Lebesgue swoimi pracami na temat całki.
Podstawowe własności miary
Zastanawiając się jakie cechy powinna posiadać „dobra” funkcja miary najlepiej jest rozważać wspomniane wyżej „miary” naturalne takie jak: objętość, długość, waga. Dobrze skalibrowana waga nigdy nie pokazuje wartości ujemnych. Taka waga powinna wskazać zero jeżeli nic nie ważymy. Ponadto, jeżeli ważmy różne produkty, oczekujemy łącznej wagi równej sumie wag poszczególnych produktów. Idąc jeszcze dalej, jeśli podzielimy ważony element na części, które można zważyć, również oczekujemy zgodności odpowiednich pomiarów.
Co możemy mierzyć
Na tym etapie rozważmy dowolny niepusty zbiór $\Omega$. Mówiąc o pomiarach na zbiorze $\Omega$ będziemy myśleli o pomiarach na jego podzbiorach $\big(\Omega$ jest „maksymalnym” zbiorem podlegającym pomiarowi – np. może to być cała płaszczyzna $\mathbb{R}^2\big)$ – niech zatem $\mathfrak{F}$ oznacza rodzinę mierzalnych podzbiorów zbioru $\Omega$. Od takiej rodziny mierzalnych zbiorów oczekujemy spełnienia jedynie 3 warunków:
- Możemy zmierzyć „nic” – tzn. zbiór pusty jest mierzalny, co zapiszemy $\emptyset \in \mathfrak{F}$
- Jeżeli możemy zmierzyć zbiór $A$, możemy również zmierzyć to co pozostało (tzn. $\Omega \setminus A$), co zapisujemy $\big(A \in \mathfrak{F} \big) \Rightarrow \big( \Omega \setminus A \in \mathfrak{F} \big)$
- Jeśli dysponujemy wieloma zbiorami, które można zmierzyć, to o ile można je ponumerować, również można zmierzyć ich sumę, co zapisujemy $\big(A_i \in \mathfrak{F}$ dla $i=1,2,\ldots \big) \Rightarrow \bigg(\displaystyle \bigcup_{i =1}^\infty A_i \in\mathfrak{F}\bigg)$
Powyższe warunki (i ich konsekwencje) określają jakiego typu podzbiory przestrzeni $\Omega$ mogą zostać zmierzone. Oczekuje się, że jeżeli można zmierzyć podzbiór, to można również zmierzyć jego dopełnienie. Jeżeli można zmierzyć wiele podzbiorów przestrzeni, można również zmierzyć ich sumę, jak też ich część wspólną. Ponadto, jeżeli można zmierzyć dwa dowolne podzbiory przestrzeni, można również zmierzyć ich różnicę. W szczególności zakłada się, że możliwe jest dokonanie pomiaru na zbiorze pustym, jak też na całej przestrzeni. Rodziny $\mathfrak{F}$ podzbiorów zbioru $$\Omega$$ spełniające powyższe warunki nazywa się sigma-ciałami.
Funkcja miary zbioru
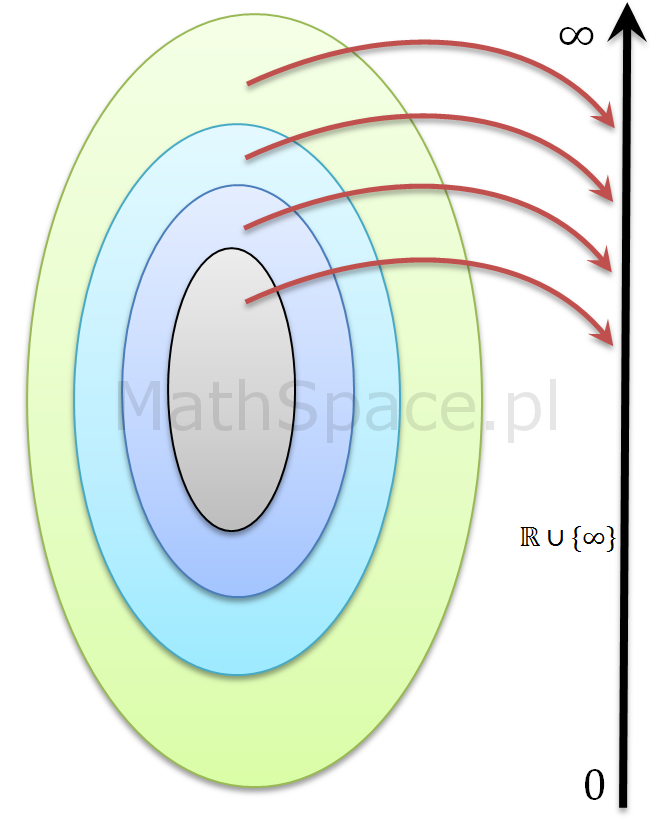
Miarą zbioru nazwiemy funkcję, która każdemu zbiorowi, który można zmierzyć (elementy sigma-ciała), przyporządkuje wartości liczbowe (również nieskończoność) spełniające poniższe 3 warunki:
- Miara zbioru ($\mu$) nie przyjmuje wartości ujemnych, ale może być zerowa, co zapisujemy $\forall ~A \in \mathfrak{F}$, $\mu(A) \mathfrak{\geq} 0$
- Miara „nic” jest zawsze równa 0, co zapisujemy $\mu(\emptyset)=0$
- Jeśli podzielimy zbiór na rozłączne części, to miara zbioru jest równa sumie miar jego części, co zapisujemy $\big( A_i \cap A_j = \emptyset \quad \mathrm{dla} \quad i \ne j \big) \Rightarrow \Bigg( \mu \bigg(\bigcup_{i = 1}^\infty A_i \bigg) = \sum_{i = 1}^\infty \mu(A_i) \Bigg)$
Powyższe warunki są wystarczające, aby funkcja miary zbioru dodatkowo spełniała poniższe:
- Miara podzbioru jest nie większa niż miara wyjściowego zbioru, co zapisujemy $\big( A \subseteq B \big)$ $\Rightarrow$ $\big( \mu(A) \leq \mu(B) \big)$
- Dodatkowo $\big( A \subseteq B \big)$ $\wedge$ $\big( \mu(B) < +\infty \big)$ $\Rightarrow$ $\big( \mu(B \setminus A) = \mu(B) – \mu(A) \big)$

Miara zbioru (i ogólnie mierzalność) jest zupełnie podstawowym pojęciem w probabilistyce, to właśnie na przestrzeniach mierzalnych oparty jest cały model probabilistyczny, a w konsekwencji też model statystyczny. Wykorzystując okazję serdecznie polecam niesamowitą książkę Patrick’a Billingsley’a pod tytułem „Prawdopodobieństwo i miara”.
Miara Lebesgue’a
W kolejnych artykułach przedstawimy miarę Lebesgue’a, która stanowi podstawę określania rozmiarów zbiorów w przestrzeniach euklidesowych.
Pozdrawiam,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.