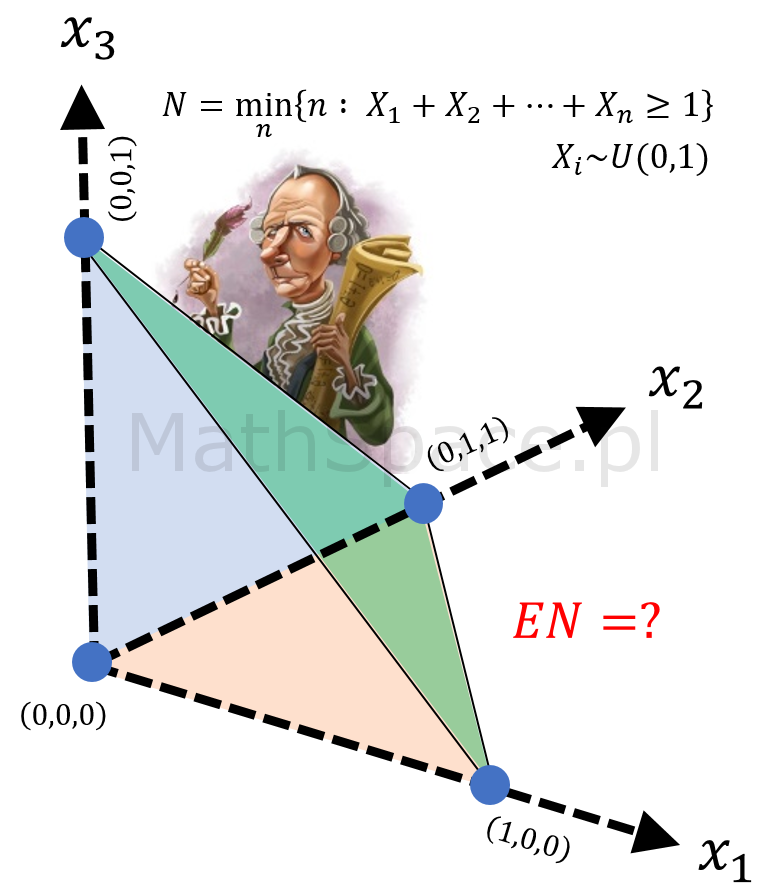
Rozkład jednostajny na odcinku $(0,1)$, chyba najprostszy z możliwych rozkładów ciągłych, z pozoru niezbyt interesujący, a jednak 🙂 Dziś ciekawostka wiążąca rozkład sumy rozkładów jednostajnych z liczbą Eulera e.
Rozkład jednostajny ciągły na odcinku (a,b)
Rozkład jednostajny ciągły na odcinku $(a,b)$ jest opisany poniższą funkcją gęstości.
$$f(x)=\begin{cases}\frac{1}{b-a}&&\text{dla }a\leq x\leq b\\0&&\text{w p.p.}\end{cases}$$
Pisząc $X\sim U(a,b)$ oznaczamy, że zmienna losowa $X$ ma rozkład jednostajny ciągły na odcinku $(a,b)$. Jest to rozkład ciągły, zatem przyjęcie wartości $0$ lub $\frac{1}{b-a}$ w punktach $x=a$ i $x=b$ jest umowne i nie ma zwykle wpływu na własności i rozważania.