
Motywacja
Niemal w każdej literaturze z zakresu statystycznej analizy danych, czy też ogólnie analizy danych, spotkać można mniej lub bardziej zaawansowane wykorzystanie terminu zmiennej losowej. Jak sama nazwa wskazuje zmienna losowa stosowana jest typowo tam gdzie zachodzi potrzeba systematyzacji pojęcia cechy losowo obserwowanego obiektu, jego atrybutów, czy też posiadanych własności. Na tym proste intuicje jednak się kończą, szczególnie gdy zaczynamy rozpatrywać rozkłady wskazanych zmiennych, porównując je między sobą, starając się sformułować mniej lub bardziej czytelne wnioski.
Ale o co tak naprawdę chodzi? Dlaczego, w dobie tak szeroko dostępnej informacji w internecie, zdecydowałem się napisać kilka słów o sekretach zmiennych losowych? Motywacja pojawiła się po szeregu rozmów z moimi kolegami po fachu, gdzie okazało się, że jeden wniosek, jedno twierdzenie, często interpretujemy inaczej, może nie diametralnie inaczej, ale jednak pojawiające się różnice dotyczyły fundamentalnych kwestii takich jak „o które prawdopodobieństwo tu chodzi”, czy też „a w jakiej przestrzeni probabilistycznej faktycznie jesteśmy”, lub „jaka jest faktycznie natura zmienności losowej i czego ta zmienność dotyczy”. Zdałem sobie sprawę, że wspomniane różnice wynikają z częstych uproszczeń stosowanych przez autorów różnych opracowań, resztę załatwia pozorna łatwość interpretacji szeregu pojęć, których zrozumienie wymaga wnikliwej obserwacji struktury matematycznych obiektów.
Do kogo adresowany jest cykl? Pomimo, że niemal wszędzie będą prezentowane intuicje i przykłady, to do pełnego zrozumienia potrzebujesz zapoznać się z pojęciami: miary, przestrzeni mierzalnej oraz przestrzeni probabilistycznej. Będę podawał większość niezbędnych definicji, zakładam jednak, że czytelnik zna podstawy teorii mnogości oraz przestrzeni metrycznych.
Uwaga – cykl jest refleksją nad modelem probabilistycznym – pewne subtelności można zauważyć dopiero w szczegółach, a jak wiemy z polskiego przysłowia, możemy tam spotkać nawet diabła 🙂
Model probabilistyczny – kilka słów
Rozkwit probabilistyki jako teorii był możliwy dzięki osiągnięciom w innych gałęziach matematyki, szczególnie w dziedzinie teorii miary i całki. Należy jednak pamiętać, że u podstaw większości współczesnych dyscyplin leży również teoria mnogości – dział matematyki, a zarazem logiki matematycznej, zapoczątkowany przez niemieckiego matematyka Georga Cantora pod koniec XIX wieku – oraz topologia.
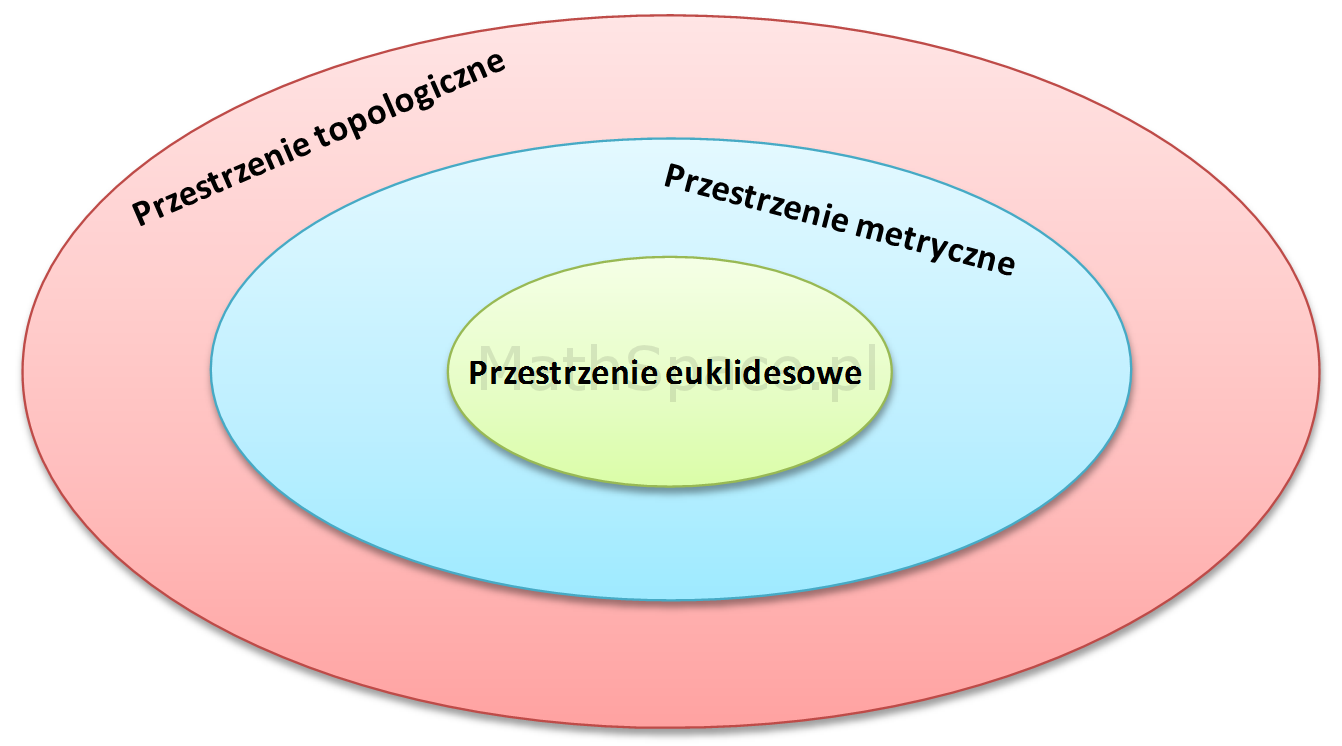
W dzisiejszych czasach każdy matematyk (i nie tylko) w sposób naturalny
posługuje się takimi terminami jak zbiór, funkcja czy relacja – nic w tym dziwnego – te pojęcia to esencja teorii mnogości zarazem będąca filarem nauk ścisłych. Nietrudno więc o wniosek, że dziedzina dla matematyki jest tym czym fizyka cząstek elementarnych dla większości nauk przyrodniczych. Ponadto okazało się, że wiele własności obiektów studiowanych w analizie matematycznej (np. ciągłość funkcji) może być scharakteryzowanych bardziej uniwersalnie przy użyciu jedynie własności zbiorów otwartych, bez potrzeby odwoływania się do podstawowego pojęcia odległości pomiędzy punktami. W tym miejscu pojawia się topologia, której domeną jest badanie takich zbiorów. Poniżej wymieniam główne pojęcia wykorzystane w rachunku prawdopodobieństwa i należące do wymienionych wyżej bardziej ogólnych gałęzi:
- Teoria mnogości
- Zbiór
- Relacja
- Funkcja
- Teoria miary i całki
- Zbiór mierzalny
- Miara zbioru
- Funkcja mierzalna
- Całka Lebesgue’a
- Topologia
- Zbiór otwarty
- Zbiór borelowski
- Probabilistyka
- Prawdopodobieństwo
- Zmienna losowa
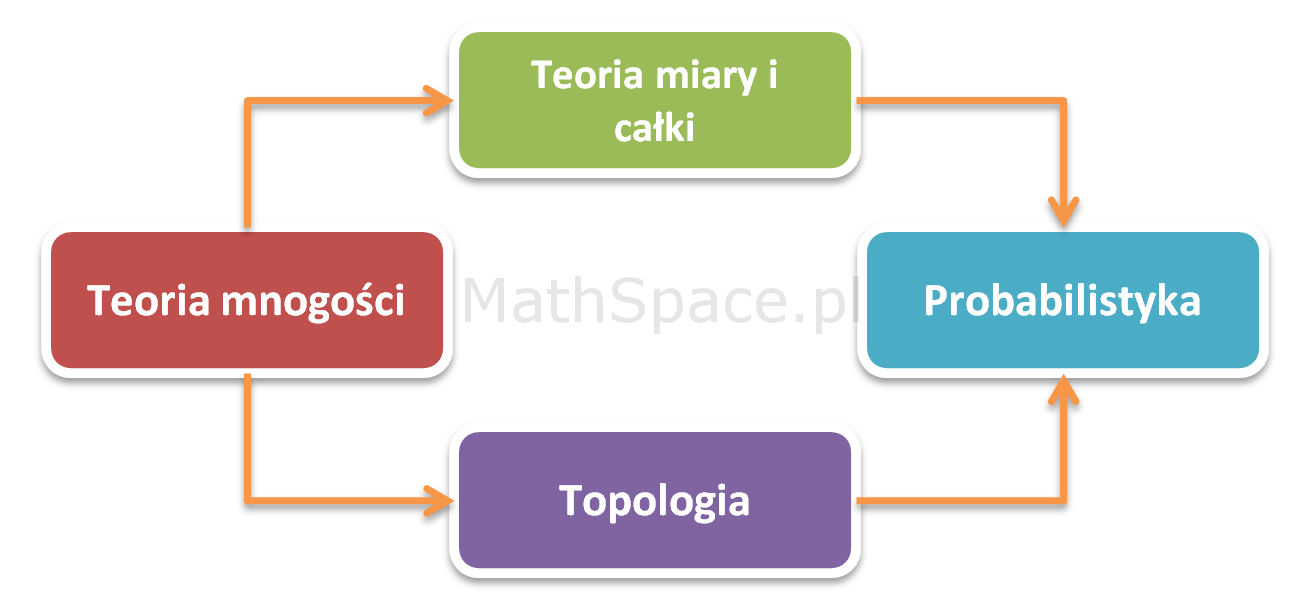
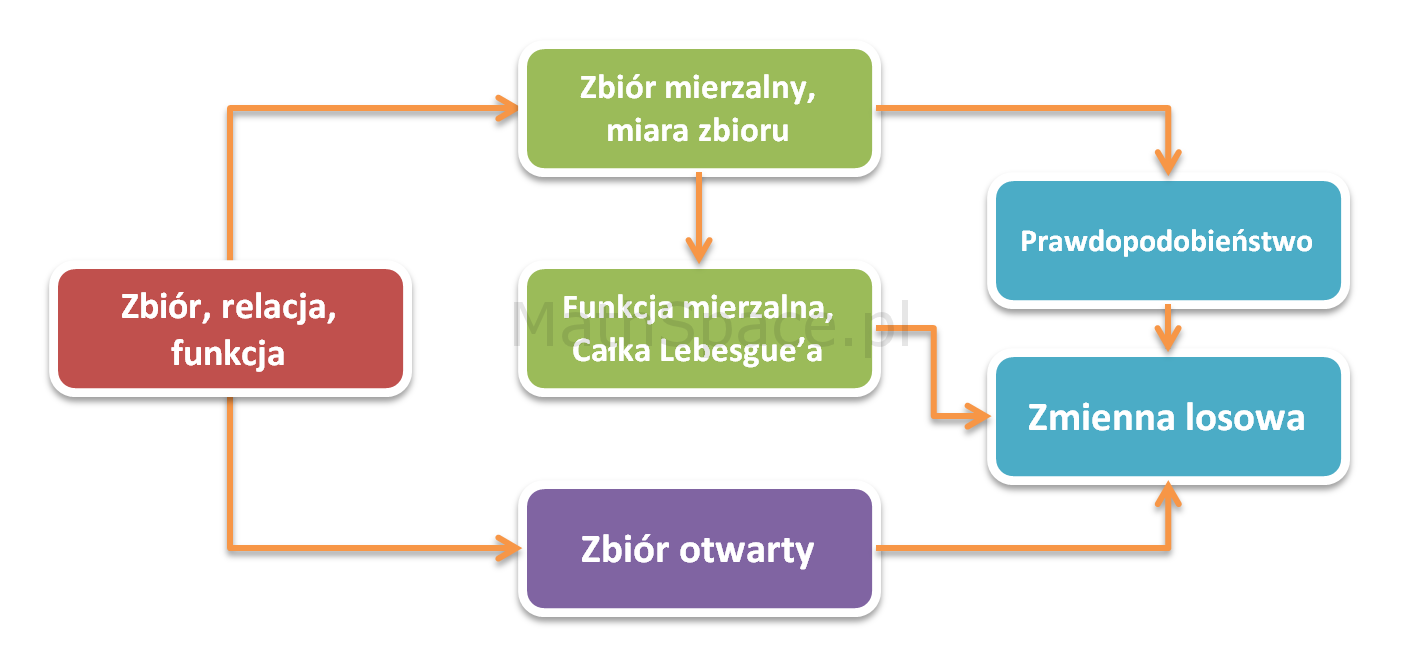
Teoria mnogości, topologia oraz teoria miary i całki to mistrzowsko opracowane dziedziny, które stanowiąc fundament probabilistyki, sprawiają, że ta ostatnia jest jedną z najpiękniejszych dyscyplin w matematyce – uwaga – jest to prywatne zdanie autora! 🙂
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

