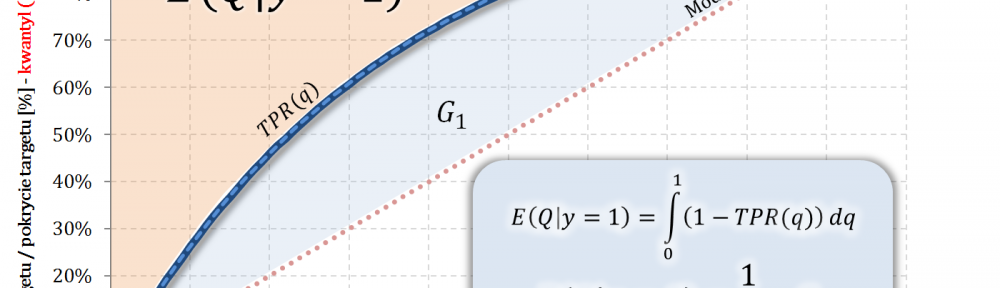W trakcie minionej nocy, około godziny 02:00, miałem nagły przebłysk 🙂 Jakoś tak, nie wiem dlaczego, przypomniałem sobie pewną zależność dla wartości oczekiwanej zmiennej losowej o wartościach nieujemnych. Zdałem sobie sprawę, że na tej podstawie, jestem w stanie opracować twierdzenie dotyczące wskaźnika Giniego (dla modelu predykcyjnego), dające elegancką postać oraz łatwe narzędzie jego estymacji. Wzór, który wyprowadziłem, bazuje na wartości oczekiwanej, dającej się z powodzeniem przybliżyć średnią (np. w SQL). Zaczynamy część #19 cyklu „Ocena jakości klasyfikacji”, jest to „hardcorowy” wpis z serii „Tips & Tricks na krzywych” 🙂 Zapraszam!
Zmienna losowa reprezentująca rząd kwantyla (pozycję) elementu w populacji
- Niech będzie dana zmienna losowa $Q\in[0;1]$, której wartość reprezentuje rząd kwantyla odpowiadający danemu elementowi, gdzie porządek jest dany malejącą oceną modelem. Inaczej – $Q$ to frakcja bazy.
- Niech $y\in\{0,1\}$ oznacza klasę faktyczną.
- Rozważmy zmienne losowe: $Q|y=1$ oraz $Q|y=0$.
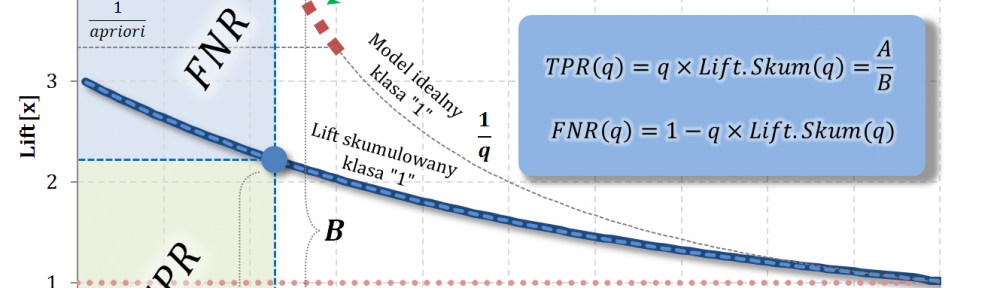
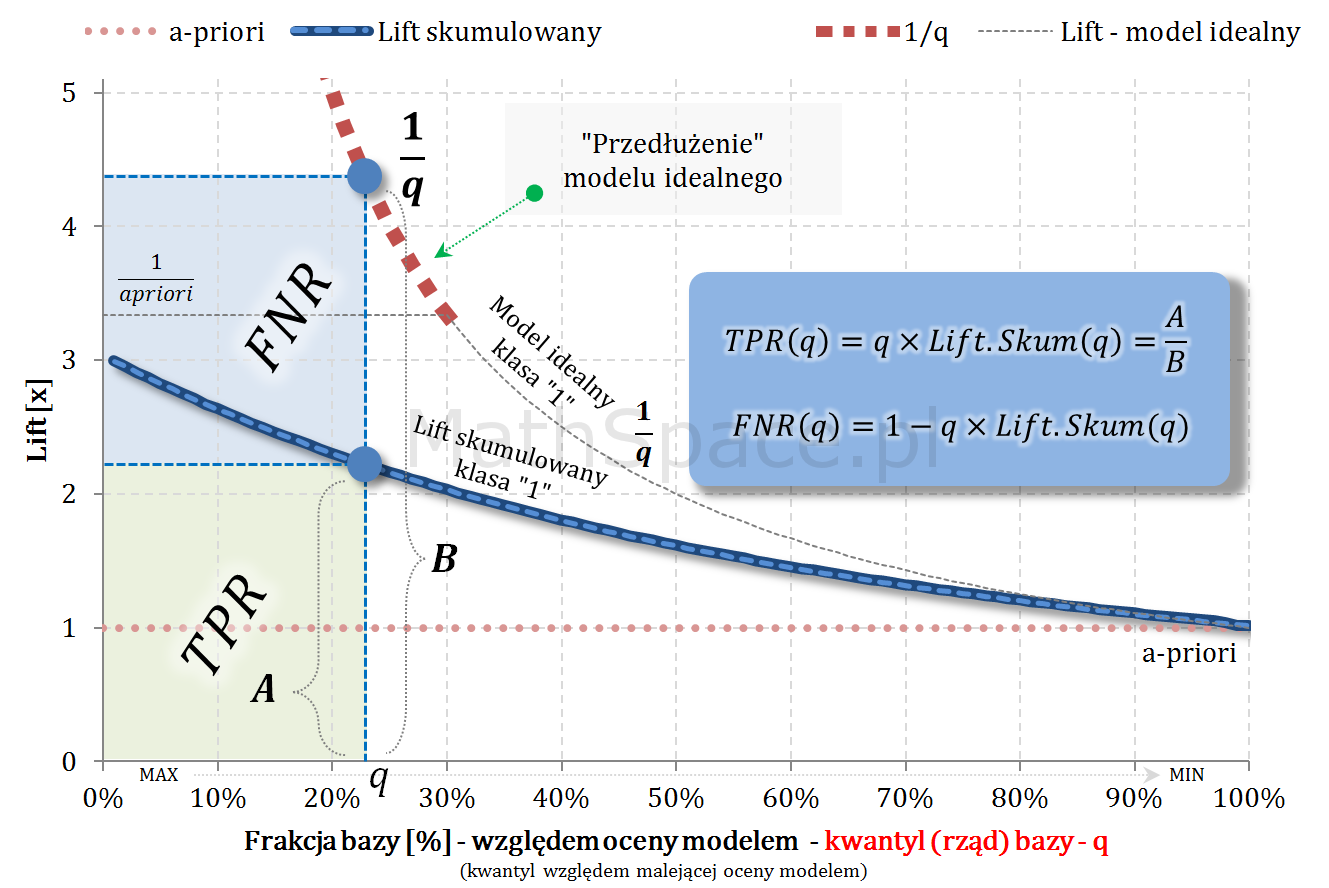
- W częściach #13 oraz #14 wykazałem, że zmienne $Q|y=1$ oraz $Q|y=0$ są opisane funkcjami gęstości podanymi przez: lifty nieskumulowane odpowiednio dla klasy „1” oraz klasy „0”.
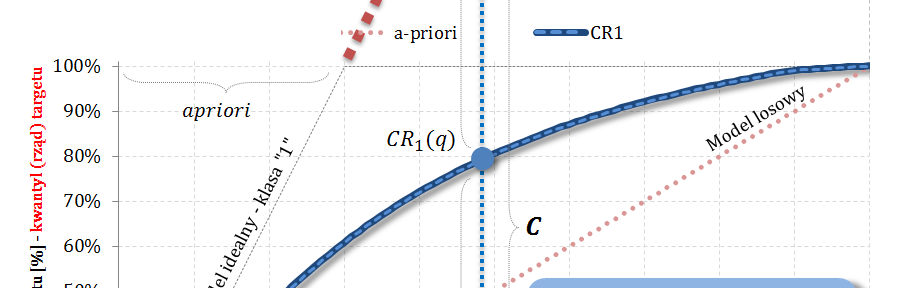
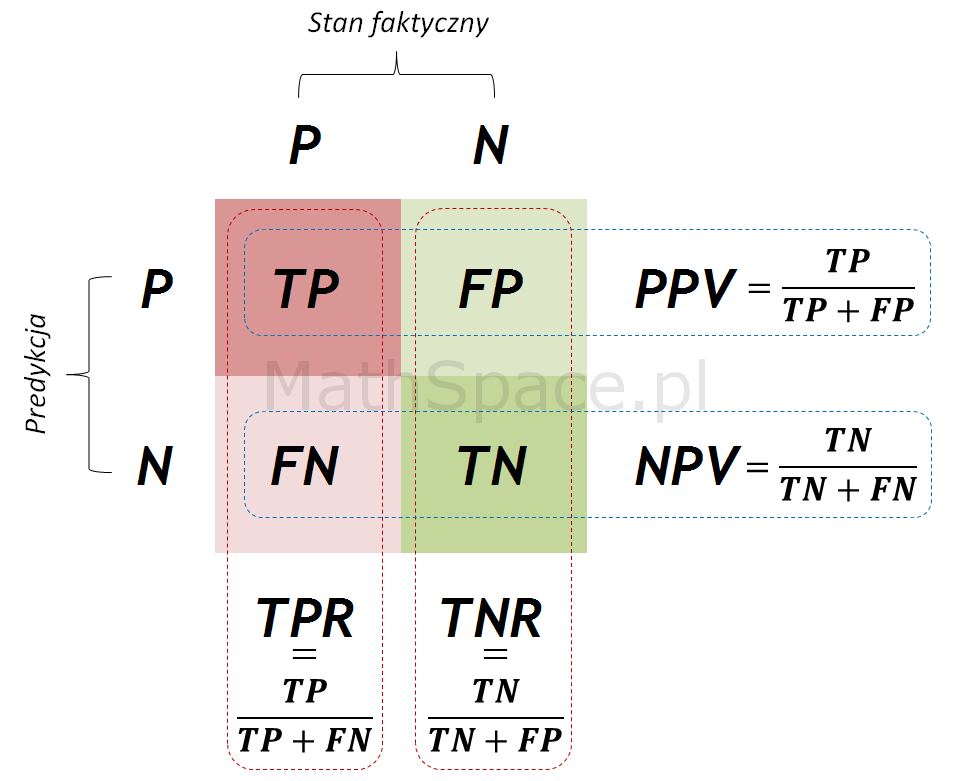
- Również w częściach #13 oraz #14 wykazałem, że zmienne $Q|y=1$ oraz $Q|y=0$ są opisane dystrybuantami podanymi przez: odpowiednio TPR dla klasy „1” oraz TNR dla klasy „0” (tam te funkcje nazywałem Captured Response).
- W części #15 wykazałem, że wskaźniki Giniego, zdefiniowane osobno dla klasy „1” oraz klasy „0”, są sobie równe – grafika poniżej.
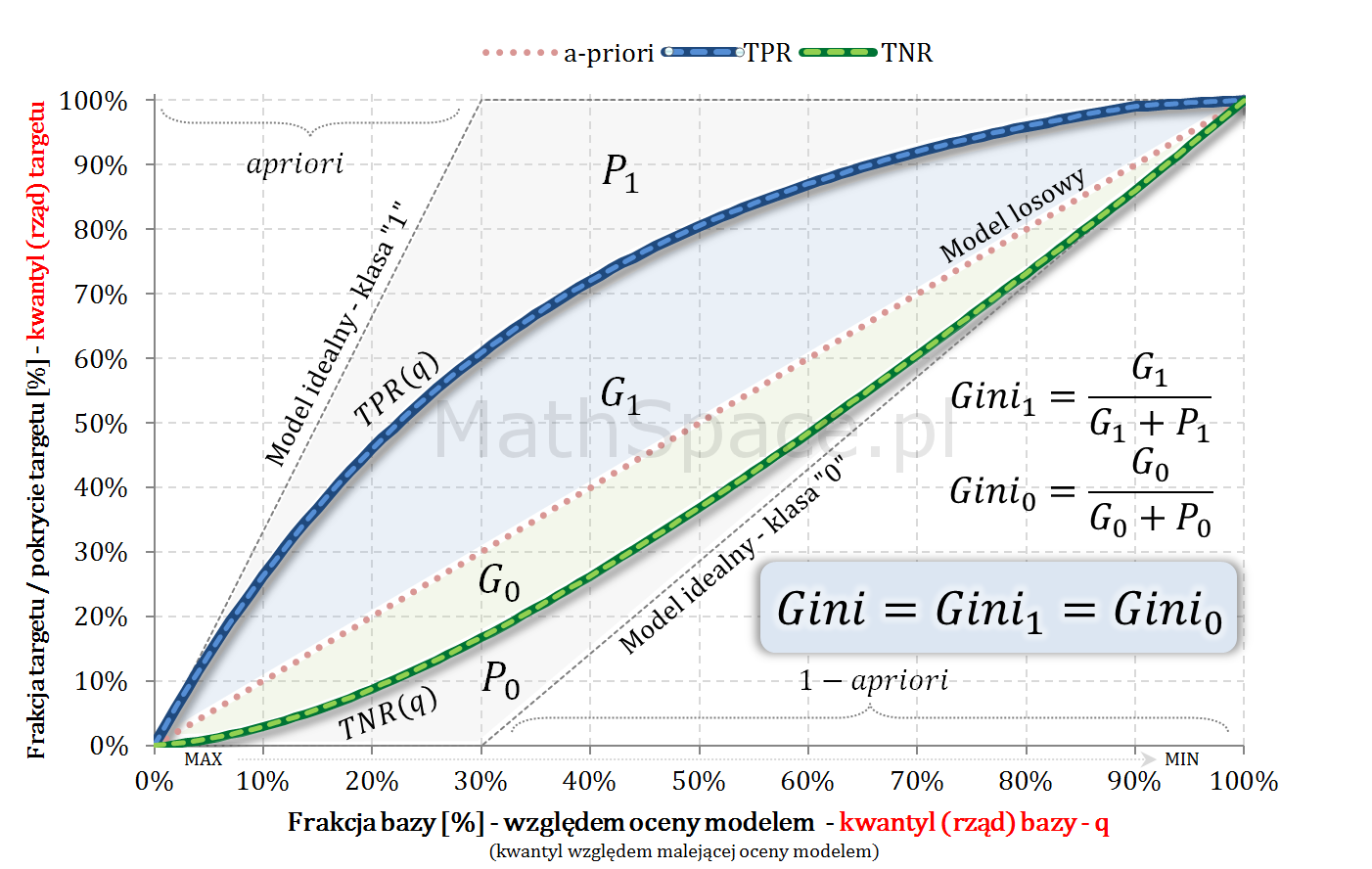
- Również w części #15 pokazałem, że
$$Gini=\frac{2G_1}{1-apriori}=\frac{2G_0}{apriori}$$
- Z powyższego, po drobnych przekształceniach
$$G_1=\frac{(1-apriori)\times Gini}{2}$$
$$G_0=\frac{apriori\times Gini}{2}$$
Wartość oczekiwana zmienne losowej o wartościach nieujemnych
Poniższą zależność pamiętam z analizy przeżycia, gdzie średnią długość przeżycia liczono jako całkę pod funkcją przeżycia 🙂 Każda funkcja przeżycia ma postać $S(t)=1-F(t)$, gdzie $F$ to pewna dystrybuanta.
Twierdzenie: Jeśli zmienna losowa $X$, o ciągłym rozkładzie, przyjmuje wartości nieujemne to:
$$EX=\displaystyle\int_0^\infty P(X\geq x)dx$$
Zakładając, że $F$ jest dystrybuantą zmiennej $X$, bazując na ciągłości rozkładu, możemy zapisać
$$EX=\displaystyle\int_0^\infty \Big(1-F(x)\Big)dx$$
W takim przypadku wartość oczekiwana to pole powierzchni „nad” dystrybuantą ograniczone prostą o wartości 1.
Wskaźniki Giniego na bazie $E(Q|y=1)$
Załóżmy, że $Q|y=1$ ma rozkład ciągły, wtedy
$$E(Q|y=1)=\displaystyle\int_0^1\Big(1-TPR(q)\Big)dq$$
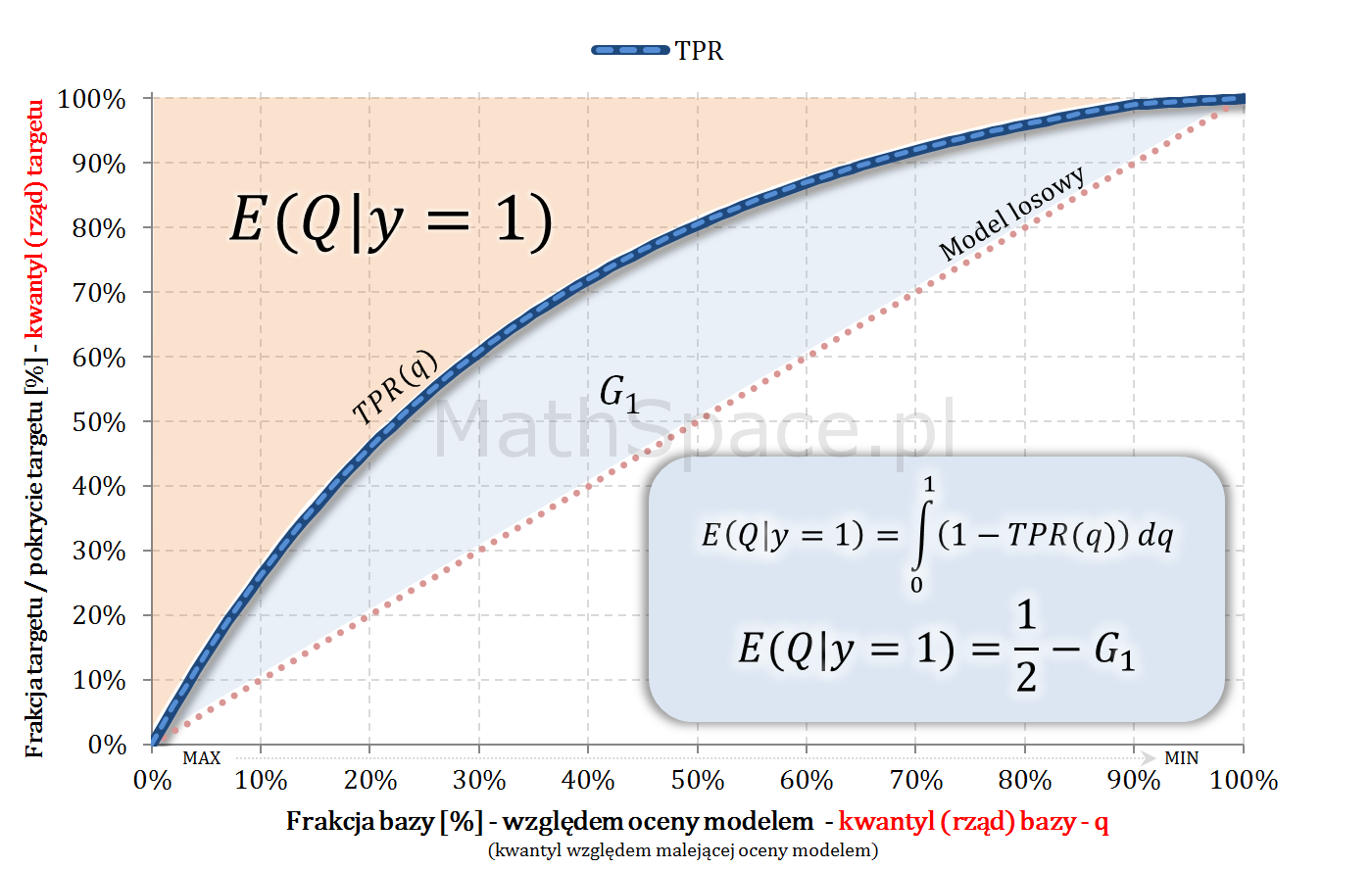
Ale
$$\displaystyle\int_0^1\Big(1-TPR(q)\Big)dq=\frac{1}{2}-G_1$$
Więc
$$E(Q|y=1)=\frac{1}{2}-G_1$$
Podstawiając
$$E(Q|y=1)=\frac{1}{2}-G_1=$$
$$=\frac{1}{2}-\frac{(1-apriori)\times Gini}{2}$$
$$E(Q|y=1)=\frac{1-(1-apriori)\times Gini}{2}$$
Przekształcając
$$2\times E(Q|y=1)=1-(1-apriori)\times Gini$$
$$(1-apriori)\times Gini=1-2\times E(Q|y=1)$$
Twierdzenie:
$$Gini=\frac{1-2\times E(Q|y=1)}{1-apriori}$$
Wow – wystarczy średni rząd kwantyla na targecie pozytywnym i apriori 🙂
Wskaźniki Giniego na bazie $E(Q|y=0)$
Załóżmy, że $Q|y=0$ ma rozkład ciągły, wtedy
$$E(Q|y=0)=\displaystyle\int_0^1\Big(1-TNR(q)\Big)dq$$
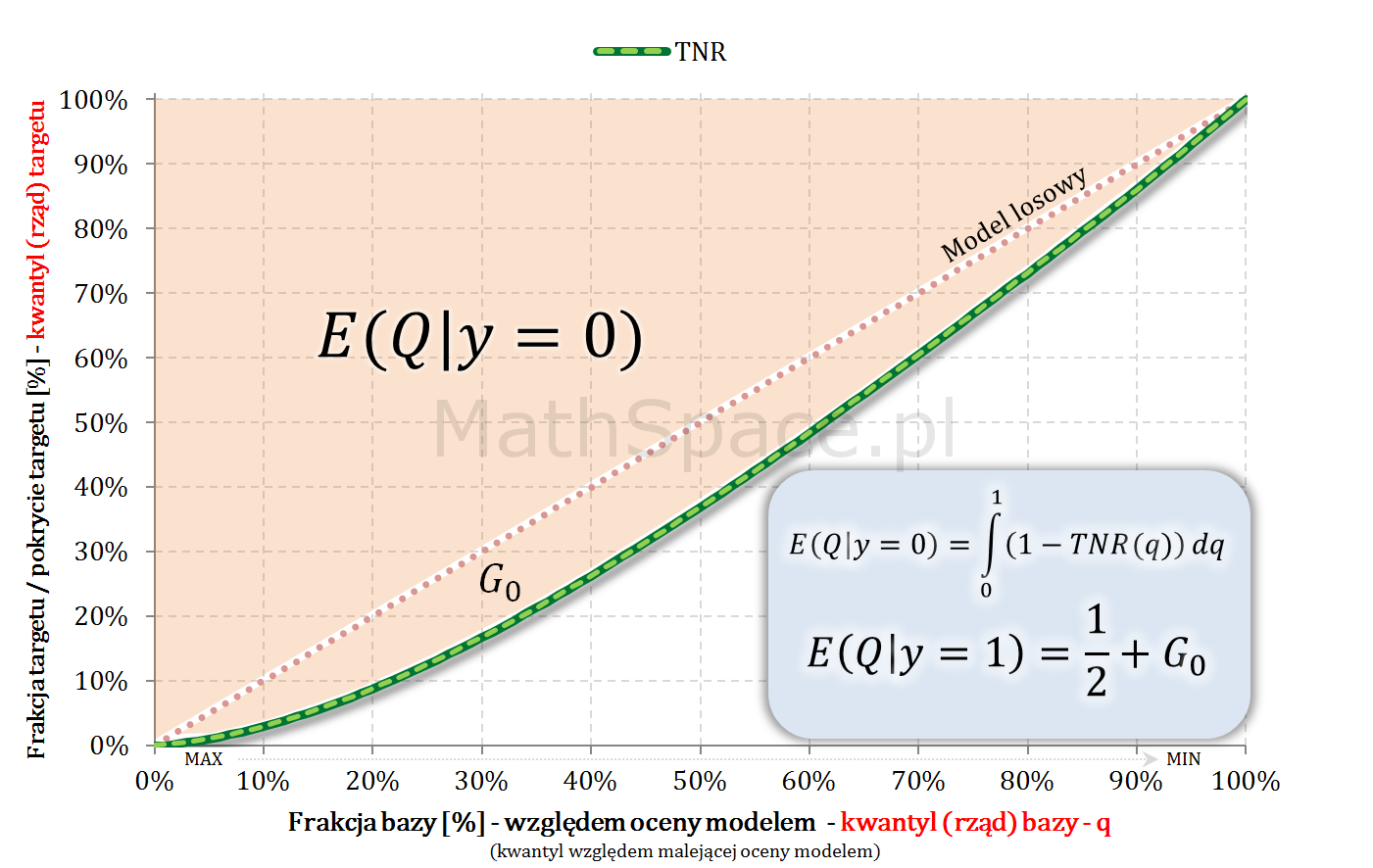
Ale
$$\displaystyle\int_0^1\Big(1-TNR(q)\Big)dq=\frac{1}{2}+G_0$$
Więc
$$E(Q|y=0)=\frac{1}{2}+G_0$$
Podstawiając
$$E(Q|y=0)=\frac{1}{2}+G_0=$$
$$=\frac{1}{2}+\frac{apriori\times Gini}{2}$$
$$E(Q|y=0)=\frac{1+apriori\times Gini}{2}$$
Przekształcając
$$2\times E(Q|y=0)=1+apriori\times Gini$$
$$apriori\times Gini=2\times E(Q|y=0)-1$$
Twierdzenie:
$$Gini=\frac{2\times E(Q|y=0)-1}{apriori}$$
Wow – tym razem wystarczy średni rząd kwantyla na targecie negatywnym i apriori 🙂
Wniosek:
$$\frac{1-2\times E(Q|y=1)}{1-apriori}=\frac{2\times E(Q|y=0)-1}{apriori}$$
Przypadki graniczne
Gini dla modelu losowego powinien wynosić 0, a dla modelu teoretycznie idealnego oczekujemy wartości 1 – sprawdźmy.

Model losowy
- $E(Q|y=1)=0.5$
- $E(Q|y=0)=0.5$
$$Gini=\frac{1-2\times E(Q|y=1)}{1-apriori}=$$
$$=\frac{1-2\times 0.5}{1-apriori}=$$
$=\frac{0}{apriori}=0$ – jest ok 🙂
$$Gini=\frac{2\times E(Q|y=0)-1}{apriori}=$$
$$=\frac{2\times 0.5-1}{apriori}=$$
$=\frac{0}{apriori}=0$ – jest ok 🙂
Model teoretycznie idealny
- $E(Q|y=1)=\frac{apriori}{2}$
- $E(Q|y=0)=\frac{aprior+1}{2}$
$$Gini=\frac{1-2\times E(Q|y=1)}{1-apriori}=$$
$$=\frac{1-2\times\frac{apriori}{2}}{1-apriori}=$$
$=\frac{1-apriori}{1-apriori}=1$ – jest ok 🙂
$$Gini=\frac{2\times E(Q|y=0)-1}{apriori}=$$
$$=\frac{2\times\frac{aprior+1}{2}-1}{apriori}=$$
$=\frac{apriori+1-1}{apriori}=1$ – jest ok 🙂
Uwaga praktyczna
Jeśli model predykcyjny zwraca dużo nieunikalnych wartości, licząc rząd kwantyla, warto zastąpić go rzędem na bazie pozycji elementu – inaczej wyniki na bazie średniej mogą być nieprzewidywalne (szczególnie dla małych apriori). Wzory testowane na realnych danych 🙂
Pozdrowienia 🙂
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.