Receiver Operating Characteristic – Krzywa ROC – geneza nazwy
Termin „Krzywa ROC” wywodzi się z teorii detekcji sygnałów, której zadaniem jest odróżnienie sygnału będącego informacją (np. sygnały z maszyn / urządzeń elektronicznych, bodźce pochodzące z organizmów żywych) od wzorców przypadkowych nie zawierających informacji (szum, tło, aktywność losowa). Pierwsze wykorzystanie krzywej ROC datuję się na okres II Wojny Światowej. Po ataku na Pearl Harbor w 1941, USA zaczęły poszukiwać lepszej metody analizy sygnałów radarowych w celu zwiększenia wykrywalności Japońskich samolotów.
Receiver Operating Characteristic – Krzywa ROC – definicja
W statystyce matematycznej krzywa ROC jest graficzną reprezentacją efektywności modelu predykcyjnego poprzez wykreślenie charakterystyki jakościowej klasyfikatorów binarnych powstałych z modelu przy zastosowaniu wielu różnych punktów odcięcia. Mówiąc inaczej – każdy punkt krzywej ROC odpowiada innej macierzy błędu (zobacz tutaj) uzyskanej przez modyfikowanie „cut-off point” (zobacz tu). Im więcej różnych punktów odcięcia zbadamy, tym więcej uzyskamy punktów na krzywej ROC. Finalnie na wykres nanosimy TPR (True-Positive Rate – oś pionowa) oraz FPR (False-Positive Rate – oś pozioma).
$c$ – punkt odcięcia
$\quad$ $c\mapsto \Big(x(c),y(c)\Big)=\Big(FPR(c),TPR(c)\Big)$
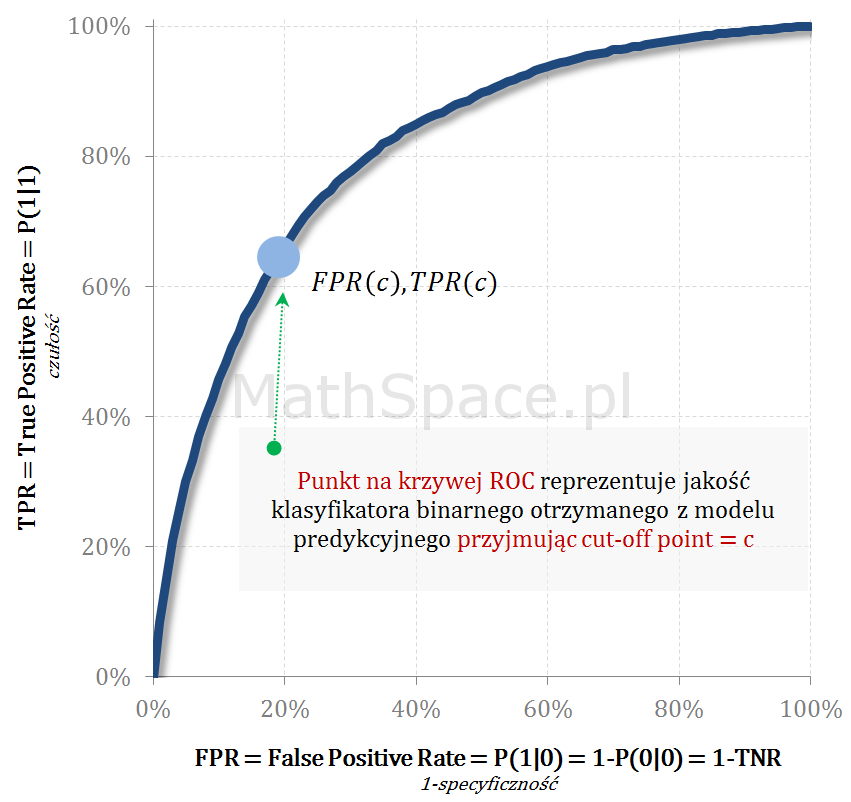
Krzywa ROC, będąc funkcją punktu odcięcia, przedstawia zmienność TPR (miary pokrycia / wychwycenia klasy faktycznie pozytywnej) w zależności od FPR (poziomu błędu popełnianego na klasie faktycznie negatywnej). Jak zawsze chodzi o pewien kompromis, tzn. dobierając „cut-off” chcemy maksymalizować TPR „trzymając w ryzach” błąd FPR. Analiza relacji TPR(FPR) jest niezwykle przydatna, ale najpierw przypomnijmy kilka podstawowych definicji.
Krótkie przypomnienie podstawowych definicji
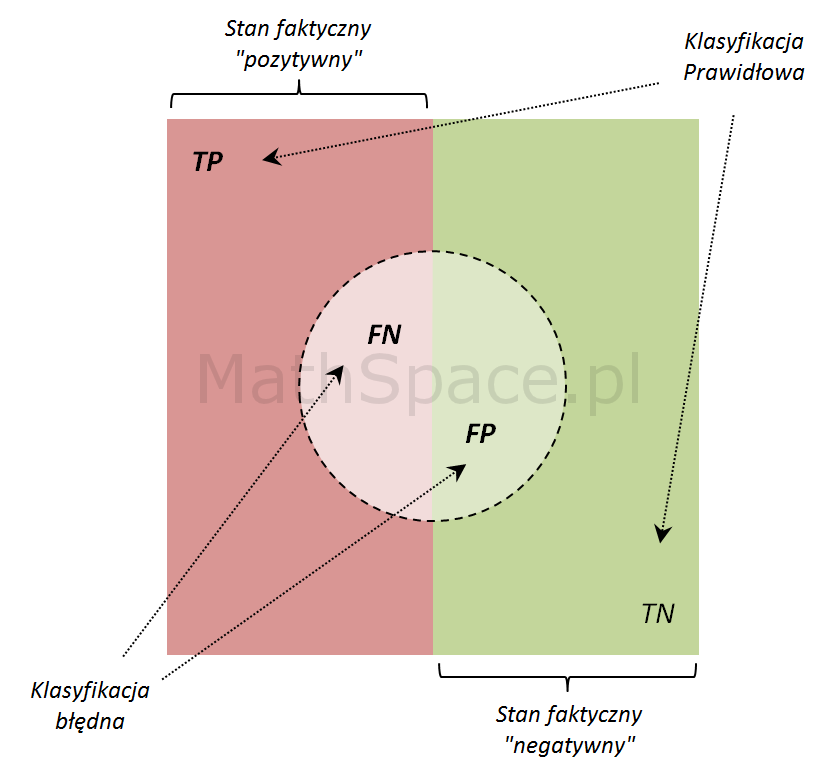
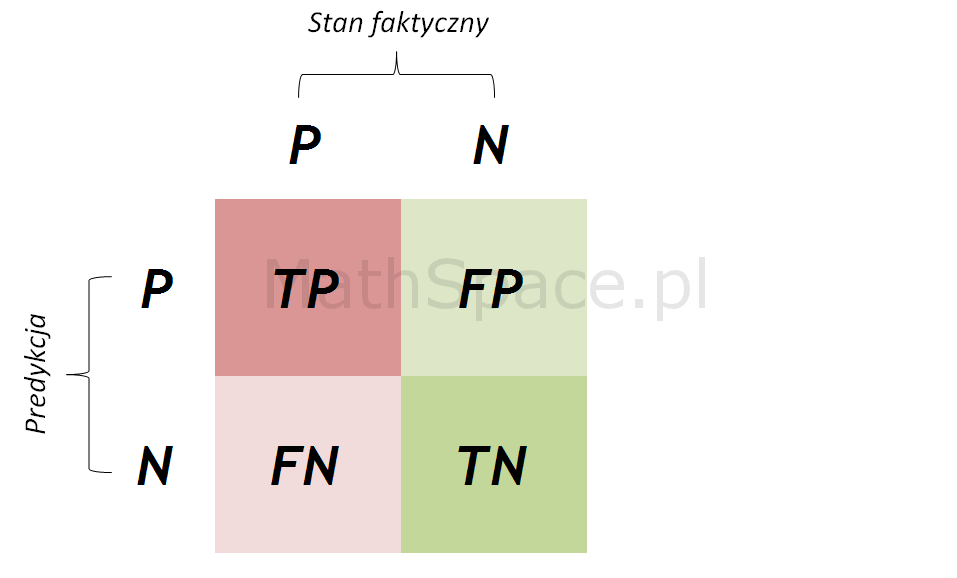
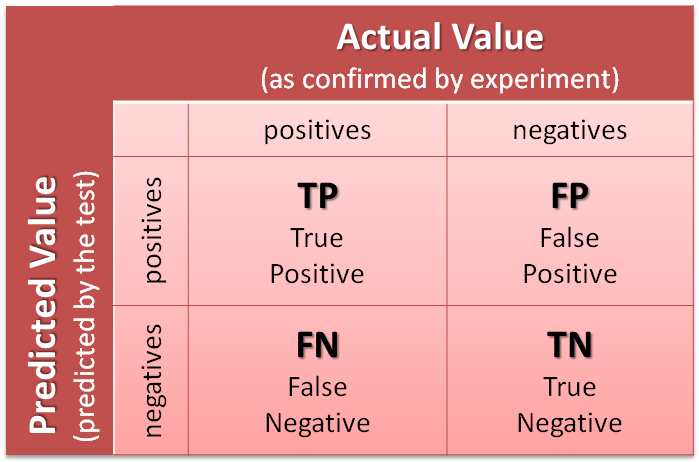
Macierz błędu
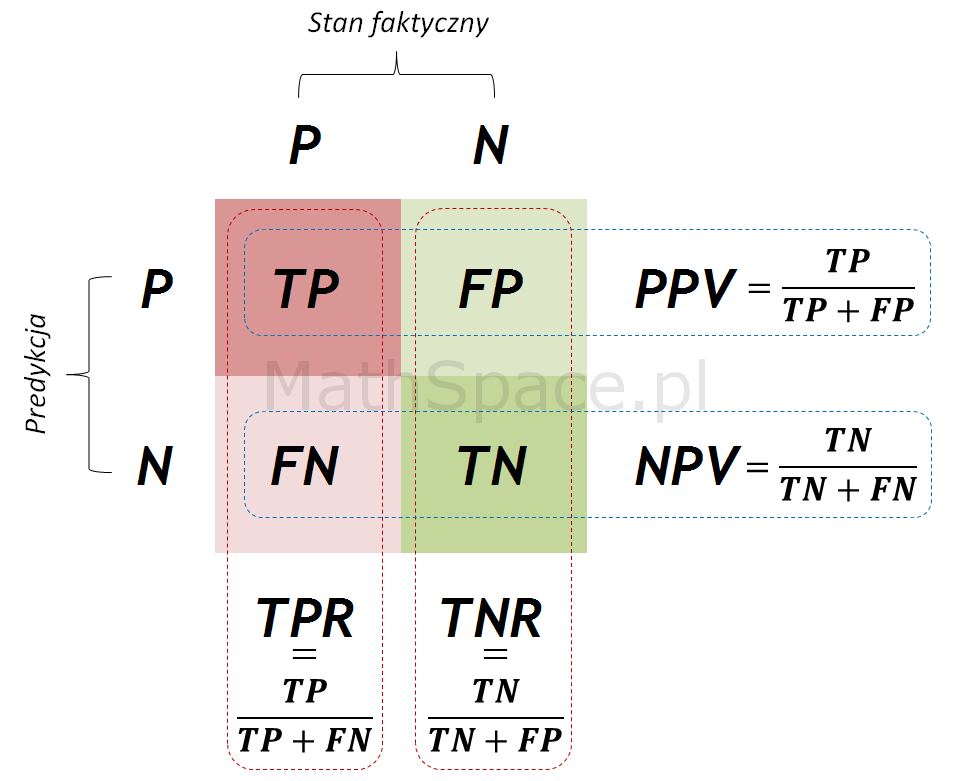
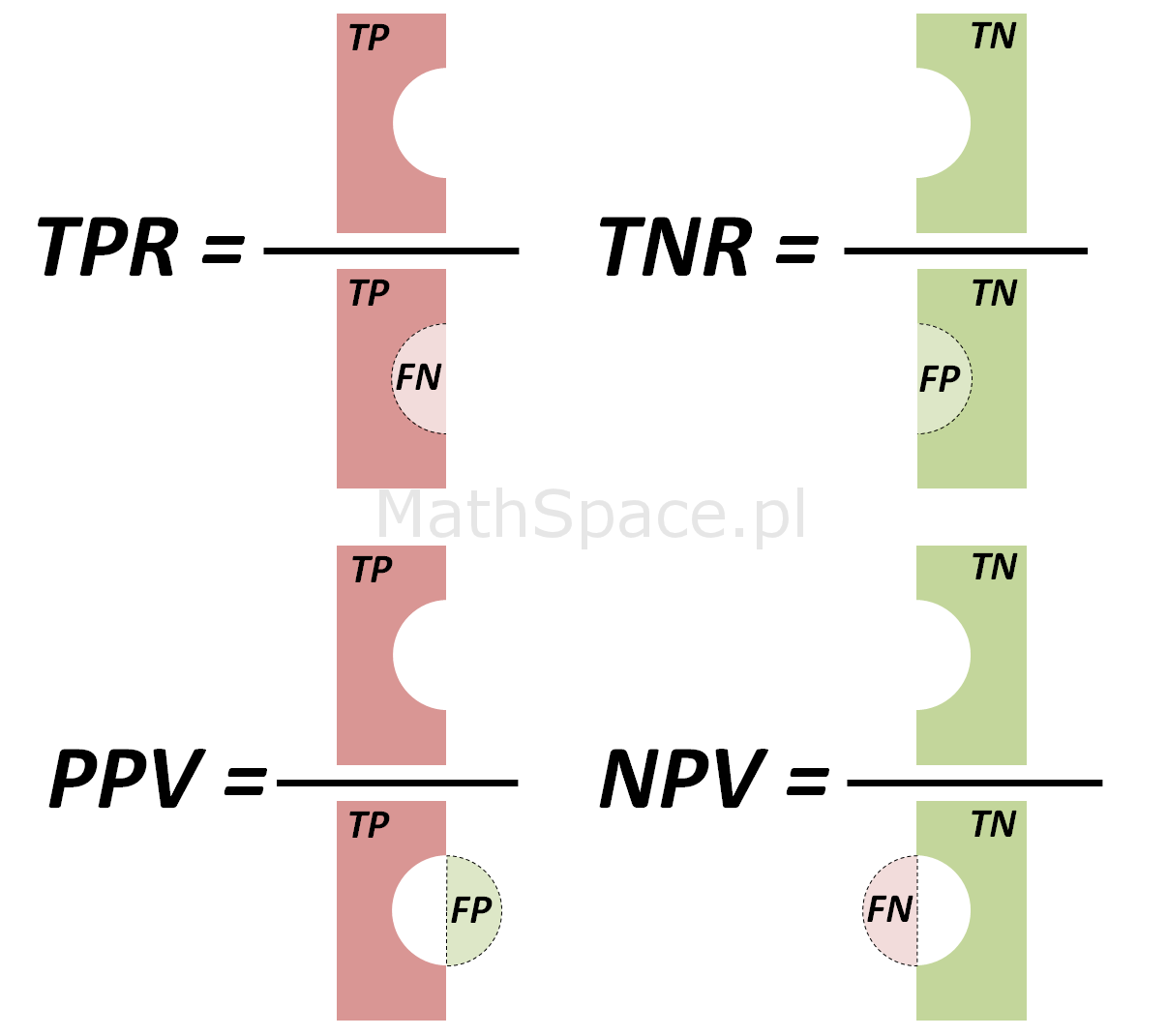
TPR True-Positive Rate (czyli czułość)
$$TPR=\frac{TP}{TP+FN}=P(pred=P|fakt=P)=$$
$$=P(pred=1|fakt=1)=P(1|1)$$
FPR False-Positive Rate (czyli 1-specyficzność)
$$FPR=\frac{FP}{FP+TN}=P(pred=P|fakt=N)=$$
$$P(pred=1|fakt=0)=P(1|0)=1-P(0|0)=1-TNR$$
Interpretacja ROC
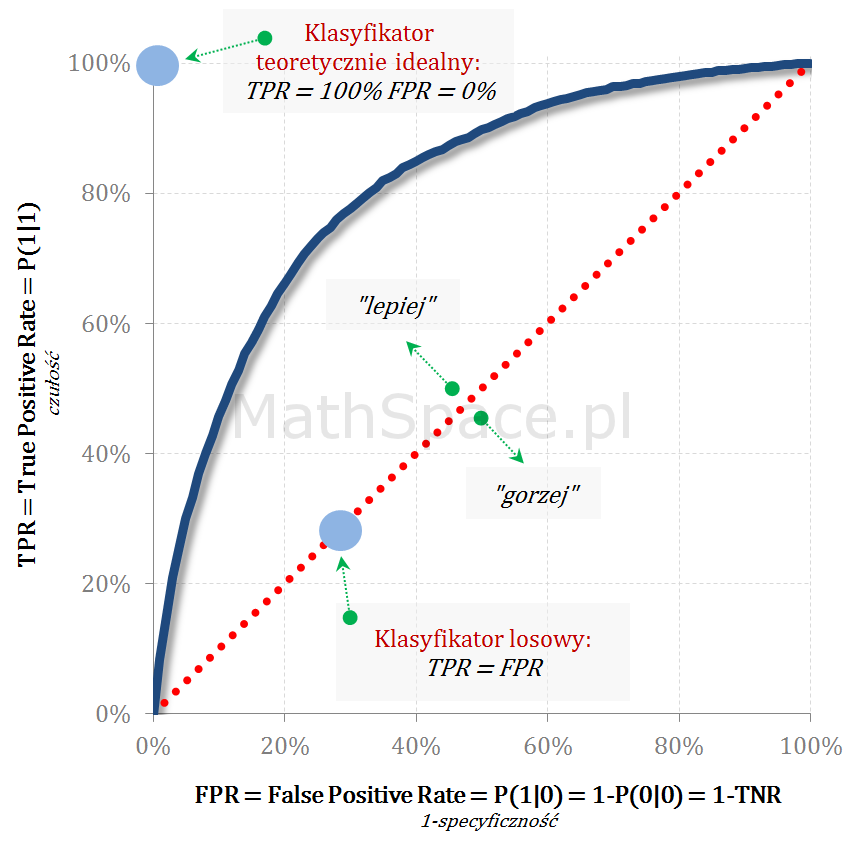
ROC – Klasyfikator teoretycznie idealny + Klasyfikator losowy
Klasyfikator teoretycznie idealny reprezentowany jest przez punkt (0,1), natomiast klasyfikatory powstałe z modelu losowego „leżą” na prostej TPR=FPR.
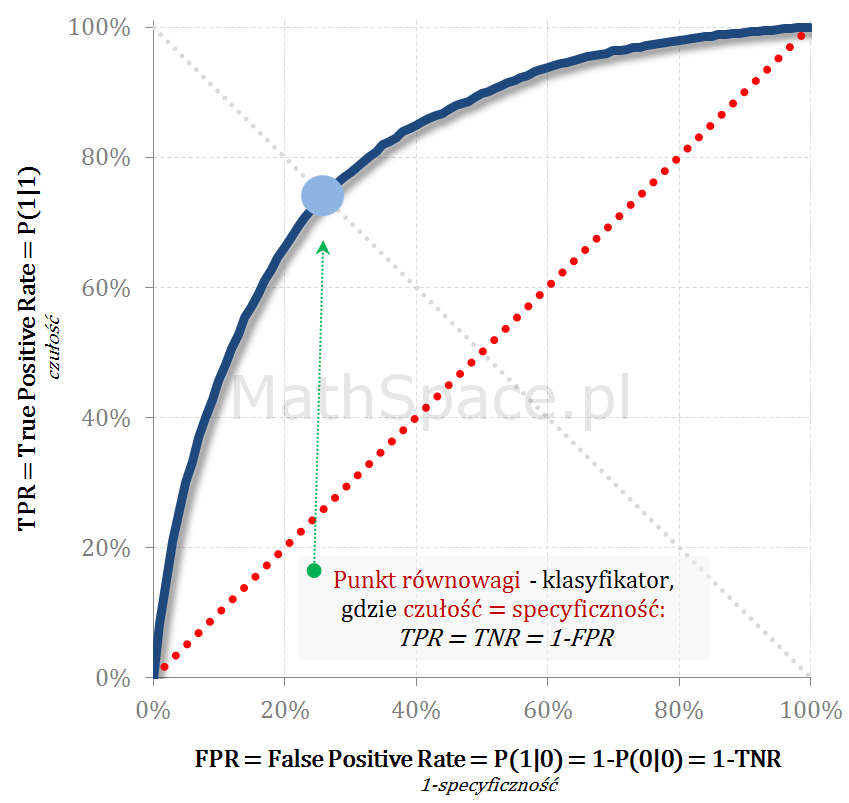
ROC – Punkt równowagi (czułość = specyficzność)
Punkt równowagi leży na przecięciu ROC z prostą TPR = 1-FPR = TNR i reprezentuje „cut-off” point, dla którego klasyfikator osiąga równowagę czułość = specyficzność.
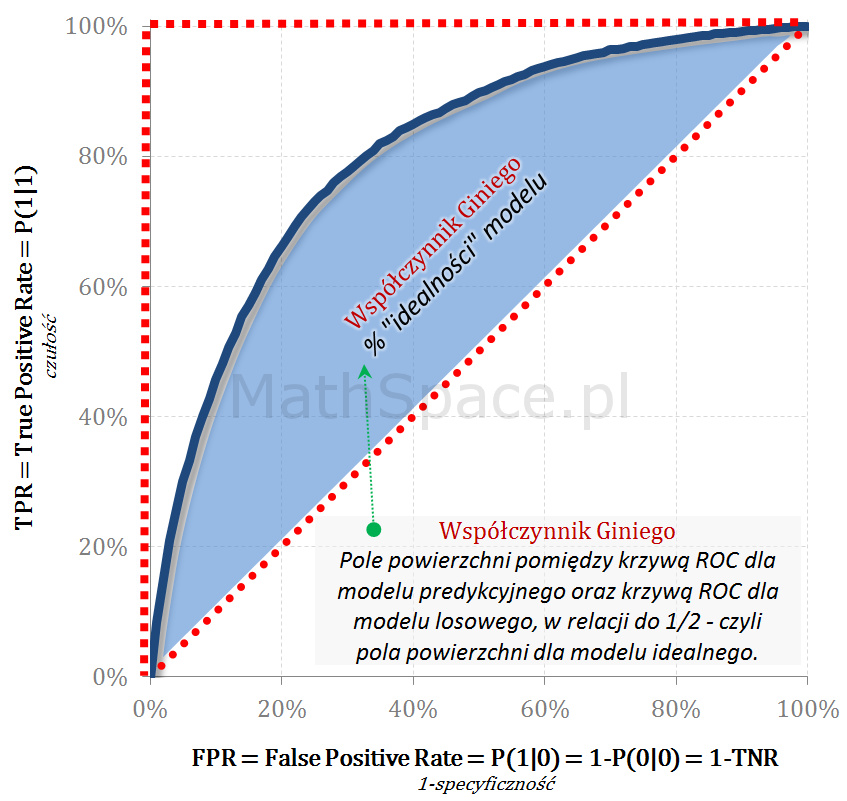
ROC – Współczynnik Giniego
Współczynnik Giniego to pole powierzani pomiędzy krzywą ROC dla badanego modelu oraz krzywą ROC dla modelu losowego w interpretacji procentowej do wartości 1/2 – czyli pola powierzchni dla klasyfikatora teoretycznie idealnego. Współczynnik Giniego jest doskonałą miarą jakości modelu i może być interpretowany jako % „idealności” danego modelu predykcyjnego.
- Im większy wskaźnik Giniego tym lepiej
- Wartość wskaźnika Giniego nie zależy od apriori (teoretycznie), w praktyce trudniej o silny model jeśli apriori jest duże
- Gini = 100% dla modelu teoretycznie idealnego
- Gini = 0% dla modelu losowego
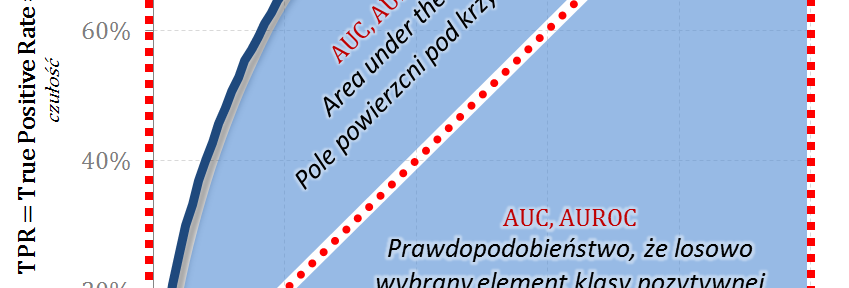
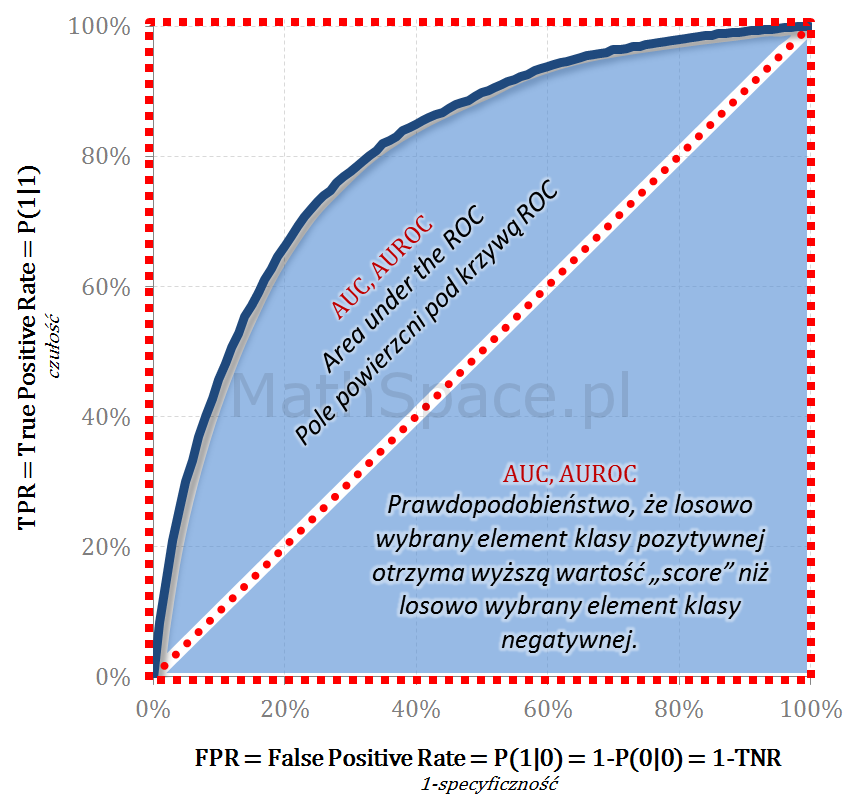
Pole powierzani pod krzywą ROC – AUC, AUROC
Tym razem wyznaczamy całość pola powierzchni pod wykresem ROC odnosząc wartość do analogicznego pola dla modelu idealnego – w tym przypadku pola kwadratu o boku 1. Interpretacja AUROC (Area Under the ROC) to prawdopodobieństwo, że badany model predykcyjny oceni wyżej (wartość score) losowy element klasy pozytywnej od losowego elementu klasy negatywnej.
- Im większy wskaźnik AUROC tym lepiej
- Wartość AUROC nie zależy od apriori (teoretycznie), w praktyce trudniej o silny model jeśli apriori jest duże
- AUROC = 100% dla modelu teoretycznie idealnego
- AUROC = 50% dla modelu losowego
- AUROC = 0% dla modelu idealnego klasy przeciwnej do pozytywnej
Ciąg dalszy nastąpi …
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.