Czy zastanawialiście się, jak język naturalny może demokratyzować technologię? Albo jak generatywna sztuczna inteligencja może wspomóc różne dziedziny biznesu – od analizy danych po zarządzanie produktem? W trakcie prezentacji zgłębiam moc kontekstu, który zmienia obecne paradygmaty. Przekonuję jak era copilot’ów wpłynie na naszą codzienną pracę. Pomagam również odkryć jakie kompetencje będą potrzebne w świecie napędzanym przez AI. Od copilota programisty, przez analityka danych, aż po CEO – dowiedz się, jak sztuczna inteligencja może stać się Twoim najcenniejszym współpracownikiem!
Continue readingAutor: Mariusz Gromada
Deep Under – RELEARN (2024)
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam Wam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia. 🙂
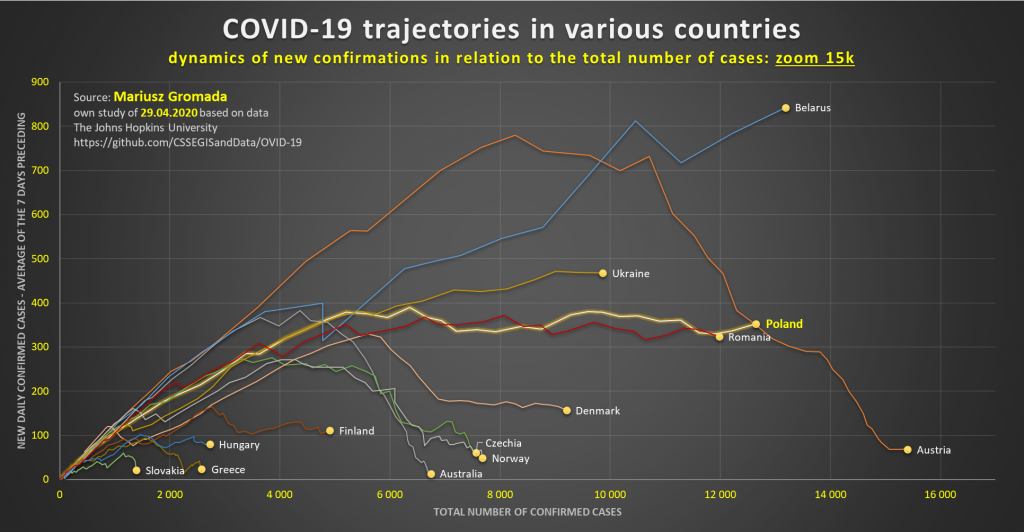
Trajektorie przebiegu COVID-19 w różnych krajach
Symulacja procesu epidemii – Grant Sanderson – 3Blue1Brown
Matematyka w obrazkach #26 – Sowa Lorenzowa :-)
W „matematyce w obrazkach” ponownie grafika wykonana na bazie Atraktora Lorenza – to bardzo wdzięczny motyw! Oto Sowa Lorenzowa 🙂

Chcesz zobaczyć poprzednie grafiki? Kliknij tutaj.
Pozdrowienia,
Mariusz Gromada
O liczbie e – Część 2 – Dlaczego jest tak „naturalna” – Funkcja wykładnicza i pochodna eˣ

„Plaża, piękna pogoda, sielanka i relaks! Różne funkcje wypoczywają. Nagle … popłoch, panika! Funkcje uciekają. Tylko jedna nadal się opala.
– Co robisz? Uciekaj! Nadchodzi operator różniczkowy!
– Nie boję się, jestem $e^x$.
I tak spokojna $e^x$ została. Wpada operator.
– Wrrr! Teraz Cię zróżniczkuję! Wrrr!
– A proszę bardzo – jestem $e^x$ – nic mi nie grozi.
– Kochana, ja różniczkuję po $dy$”
Ten iście „nerdowski” dowcip całkiem dobrze rozpoczyna kolejną część serii „o liczbie e”. Na bazie pochodnej przedstawię dodatkowe argumenty „dlaczego?” liczba e jest tak naturalna. Zaczynamy od powtórki podstaw w zakresie potęgowania. Prawdopodobnie zaskoczę Cię już samą definicją funkcji wykładniczej $a^x$ 🙂
Definicja funkcji wykładniczej na bazie potęgowania
O liczbie e – Część 1 – Dlaczego jest tak „naturalna” – Procent składany

Funkcja wykładnicza i logarytm wprowadzane są w szkole średniej (przynajmniej tak było w moim przypadku). Zazwyczaj wtedy poznajemy liczbę $e$, którą magicznie nazywa się podstawą logarytmu naturalnego.
$$e\approx 2.718\ldots$$
Nazwa dobrana jest świetnie, niestety nikt nie tłumaczy dlaczego tak właściwie jest. Cała sprawa jest niezwykle ciekawa, jej wyjaśnienie to temat nowej serii artykułów „o liczbie e”. Tym samym wzbogacam cykl „dlaczego?”. Dowody przeprowadzę „metodą elementarną” – wszak chodzi o „pierwotność / naturalność” $e$. Będzie kilka dużych „odcinków” – zapraszam 🙂
Nota historyczna
Liczba e pojawia się w wielu dziedzinach. W matematyce jest wszechobecna! Z powodzeniem dorównuje liczbie $\pi$. Analiza matematyczna (w szczególności rachunek różniczkowy i całkowy, równania różniczkowe), funkcje specjalne, analiza zespolona, rachunek prawdopodobieństwa, statystyka matematyczna – to najbardziej wyraziste przykłady. W innych naukach ścisłych (np.: ekonomia, fizyka, biologia) liczba e pojawia się w wielu ważnych równaniach, w tym: równanie przewodnictwa cieplnego, wzór barometryczny, rozpady promieniotwórcze, fazory, funkcja falowa w mechanice kwantowej, wzrost populacji, procent składany.
Pierwsze informacje na temat liczby e pojawiły się w 1618 roku. Opublikował je John Napier, przygotowując tabele logarytmów. Praca nie zawierała samej stałej, prezentowała niektóre wartości logarytmów na bazie e. Liczbę e w jej dzisiejszej postaci odkrył Jacob Bernoulli. Dokonał tego w 1683 roku analizując własności procentu składanego. Pierwsze udokumentowane wykorzystanie liczby e, wtedy oznaczanej przez b, pojawiło się w latach 1690-1691 (Gottfried Leibniz, Christiaan Huygens). Wykorzystanie stałej znacząco rozwinął Leonhard Euler oznaczając ją w 1727 roku do dziś wykorzystywanym symbolem $e$.
Procent składany
Matematyka w obrazkach #25 – Duch – Atraktor Lorenza :-)
Grafika wykonana na bazie Atraktora Lorenza – świetne wzbogacenie cyklu „Matematyka w obrazkach” 🙂

Polecam poniższą animację – 500 tysięcy ciasno upakowanych cząstek rozchodzi się w chaos. Cząstki to punkty z rozkładu Gaussa z odchyleniem standardowym 0.01. W miarę upływu czasu cząstki podążają za dynamiką Lorenza.