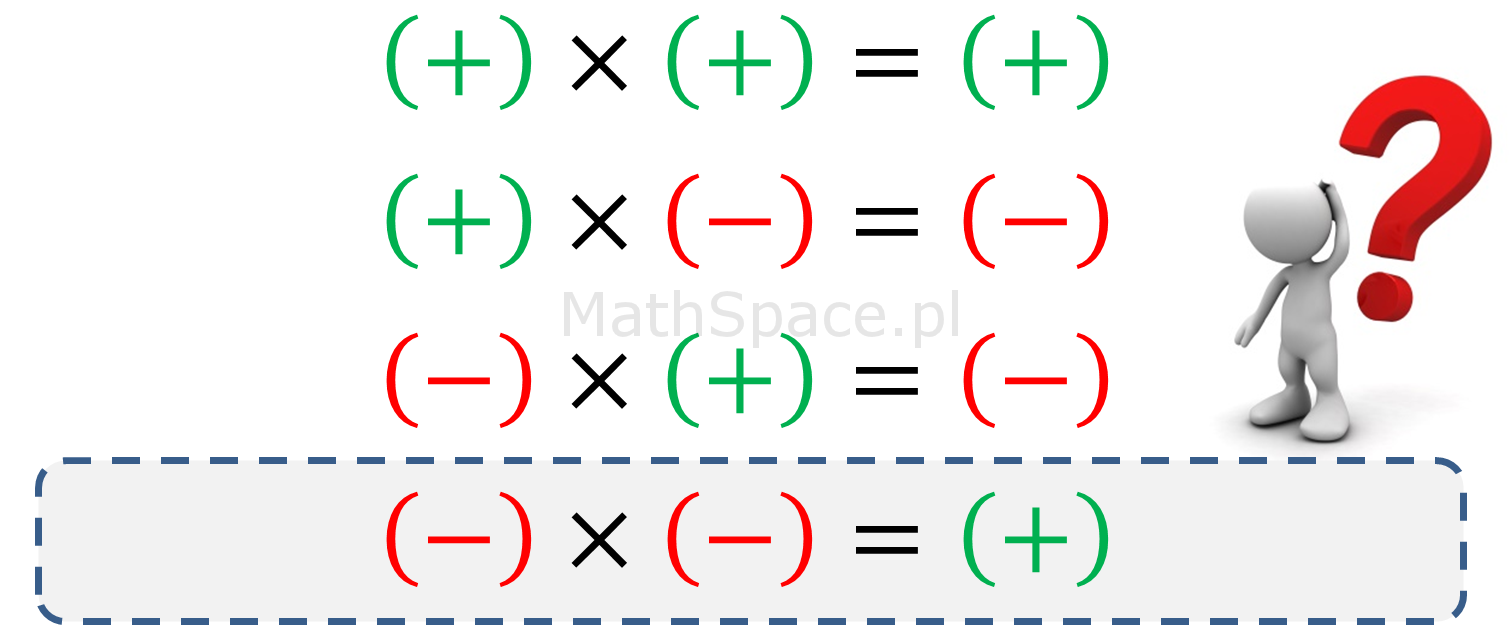
Z pewnością każdy wie, że wynikiem mnożenia liczb ujemnych jest liczba dodania. Formułka „minus razy minus daje plus” była nam wtłaczana do głów w trakcie wczesnych lat szkolnych. Nauczyciele zapomnieli jednak wyjaśnić dlaczego tak właśnie jest, oraz przybliżyć motywację matematyków definiujących arytmetykę liczb ujemnych.
Mnożenie jako skrócone dodawanie
Mówi się, że mnożenie to skrócone dodawanie, co jest w zupełności prawdą i, przy ograniczeniu do liczb całkowitych, faktem dosyć oczywistym.
$$3\times 4 = 3 + 3 + 3 + 3 = 4 + 4 + 4 = 12$$
Mnożenie jest przemienne i rozdzielne względem dodawania
Te dwie fundamentalne własności mnożenia zapisujemy jako
przemienność $a\times b = b\times a$
przykład $3\times 4 = 4\times 3=12$
rozdzielność $a\times (b+c)=a\times b + a\times c$
przykład $3\times 4 = 3\times (1+3) = 3\times 1 + 3\times 3 = 3 + 9 = 12$
Mnożenie liczb ujemnych z punktu widzenia matematyka
Matematycy, definiując arytmetykę liczb ujemnych, chcieli zachować spójność z już rozwiniętą arytmetyką liczb dodatnich i zera. Opierając się na interpretacji skróconego dodawania łatwo uzasadniamy następujące:
$$-3\times 4 = (-3)+(-3)+(-3)+(-3)=-12$$
„Dodając dług do długu” otrzymujemy większy dług – intuicyjne. Teraz wykorzystując przemienność mnożenia otrzymujemy:
$$4\times (-3)=-3\times 4=-12$$
W tym momencie z intuicją już trochę trudniej, natomiast spójność została zachowana. Czas przejść do meritum – tzn spróbujmy odpowiedzieć na pytanie:
$$-3\times (-4)=?$$
Do rozwiązania powyższego zastosujemy trick na bazie rozdzielność mnożenia względem dodawania.
$$-3\times 0=0$$
$$-3\times 0=-3\times(-4+4)=0$$
$$-3\times(-4+4)=-3\times (-4)+(-3)\times 4=0$$
$$-3\times(-4)+(-12)=0$$
$$-3\times(-4)=12$$
Powyższe z intuicją nie ma nic wspólnego, jednak jest spójne, tzn. na bazie arytmetyki liczb dodatnich i zera, przemienności mnożenia, rozdzielności mnożenia względem dodawania, jesteśmy w stanie uzasadnić dlaczego mnożenie liczb ujemnych musi być liczbą dodatnią.
Mnożenie liczb ujemnych jako zmniejszenie straty
Załóżmy, że mnożymy dwie liczby, gdzie interpretacja pierwszej to wartość zysku bądź starty, natomiast znaczenie drugiej to zwielokrotnienie (zwiększenie / zmniejszenie) pierwszej wartości. W takiej sytuacji mnożenie dwóch liczb ujemnych oznacza zmniejszenie straty, czyli łączny efekt dodatni działania.
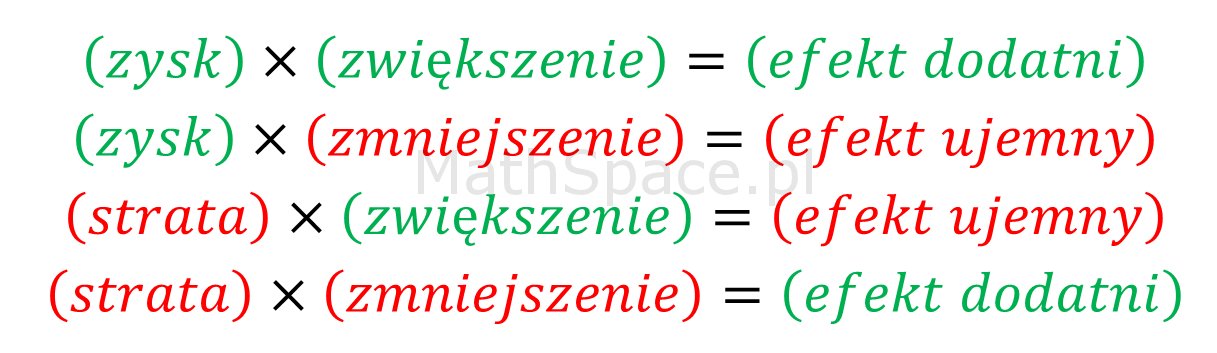
Powyższe wyjaśnienie można określić mianem intuicyjnego 🙂
I na koniec film od Mathologer’a wyjaśniający powyższy problem (materiał, na którym wzorowałem powyższy wpis).
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

Witam,
Przez niecałe 24 godziny od publikacji powyższy wpis przeczytało około 60 unikalnych użytkowników – jak widać tematyka okazała się interesująca, co mnie cieszy 🙂
Pozdrowienia,
Mariusz Gromada
Bardzo ciekawie przedstawione, jeśli chodzi o mnożenie liczb ujemnych jako zmniejszenie straty. Super!
Dzięki 🙂
Temat skopiowany z
https://www.youtube.com/watch?v=ij-EK-MZv2Q
więc kolego nie czym się chwalić
Dzięki, już dodane w tekście nawiązanie do Mathologera. Zerknij w inne moje wpisy – jeśli bazuję na czymś – staram się umieścić referencje (np. Numberphile, Vsauce).
Pozdrowienia
Totalitarność właściwości dodatnich, ujemnych i sposób ingerencji w nie poprzez siły oddziałujące na nie… Fascynujące! Ludzki osąd nie zna granic.. a ja myślałem, że domowa kłótnia kiedyś się kończy, a tu guzik prawda. Bez męskiej ręki nie poskromisz bestii.
Ty serio tak z tą ręką? (…)
Przecież to lewa ręka 🙂
Czy – × – × – × – daje plus czy minus
–
ani plus ani minus. Mamy tu dodawanie 4 liczb ujemnych:
– × – × – ×
Zatem wynik będzie ujemny: -4
ale nie żaden minus czy plus. Bo Minus i plus to tylko znak liczby, a wynikiem nie jest minus czy plus tylko albo liczba dodatnia albo liczba ujemna, w tym przypadku liczba ujemna
– × – plus
– × – plus
plus razy plus = plus
Tak 🙂
Dzięki za taki temat, bo tu nie chodzi o szkolny banał.
Mam problem z przykładem wyjaśniającym zaczynającym się od : „-3×0=0”.
Jeśli „-3” to jest strata i ta strata nie jest ani zmniejszana ani zwiększana, to powinna pozostać taka jak była czyli „-3×0=-3”. Zatem jedna kontrowersję próbuje się wyjaśnić przy pomocy innej kontrowersji.
Po drugie weźmy „-5x-5” – na zdrowy rozsądek to powinno być 20 a nie 25. Powiedzmy, że jestem winien 5 zł bankowi, ale wygrałem jakiś konkurs i bank spłaca mój dług pięciokrotnie. Wtedy odbiera swoje 5 złotych a mi daje 20 zł.
Zero to „nic”, jeśli nie mam na żadnym koncie długu, to wynosi on 0 zł. Co do -5×5, to ja tłumaczę synowi, że mam na pięciu kontach po 5 zł debetu, czyli dodaję do siebie te debety, więc wychodzi -25 zł
Po pierwsze:
Jeśli posługujemy się zaproponowanym schematem i potraktujemy działanie -3×0 jako stratę pomnożoną przez zero czyli ani nie zwiększaną ani nie zmniejszaną to rzeczywiście możemy dojść do tak absurdalnego wniosku, że -3×0=-3. Dlatego zaproponowany przez autor blogu schemat mnożenia jest błędny.
Po drugie:
Rzeczywiście, jeśli potraktować działanie -5x-5 jako mnożenie które można zastąpić skróconym dodawaniem to wynika z tego, że aby otrzymać oczekiwany wynik, czyli 25 musimy do -5 dodać 5 sześć razy:
-5 +5+5+5+5+5=25
tak, jak w działaniu 5×5 dodajemy do 5 piątkę tylko 4 razy:
5 +5+5+5+5=25
Gdybyśmy chcieli być w zgodzie z ostatnim schematem to działanie -5x-5 należy zapisać jako:
-((-5)+(-5)+(-5)+(-5)+(-5))=25
ale jest to działanie z ukrytym mnożeniem bo znak minus przed nawiasem oznacza mnożenie przez -1:
-1x((-5)+(-5)+(-5)+(-5)+(-5))=25
Wynika z tego, iż mnożenia dwóch liczb ujemnych typu -5x-5 nie da się przedstawić w czystej postaci jako skrócone dodawanie. Jest do tego potrzebna „proteza” w postaci mnożenia przez -1.
Jak sądze, jest to szczegół ważny ale pomijany w tak trywialnym, zdawałoby się temacie jak mnożenie liczb.
Oczywiście, popełniłem błąd dodając do -5 piątkę sześć razy. To działanie powinno mieć więc postać:
-5 +5+5+5+5+5+5=25
Bardzo ciekawe wyjaśnienie bazujące na intuicji. Ogólnie bardzo interesujący blog. Gratulacje Panie Mariuszu.
Zaproponuję inny schemat mnożenia może bardziej na nasze potrzeby intuicyjny.
Mnożenie jest działaniem dwuargumentowym w którym w wyniku działania mnożnej (pierwsza liczba) na mnożnik (druga) dostajemy iloczyn. Na nasze potrzeby mnożną potraktujmy jako działanie plus 1 oznaczające zachowanie stanu zysku lub straty, oraz minus 1 jako działanie zmieniające stan zysku lub straty oraz liczbę dodatnią x oznaczającą wielokrotne zwiększenie/zmniejszenie zysku/straty.
Wtedy:
x * 1 * zysk = zachowanie stanu zysku oraz jego wielokrotne zwiększenie/zmniejszenie
x * (-1) * zysk = zmiana stanu z zysku na stratę oraz jej wielokrotne zwiększenie/zmniejszenie
x * 1 * strata = zachowanie stanu straty oraz jej wielokrotne zwiększenie/zmniejszenie
x * (-1) * strata = zmiana stanu straty na zysk oraz jego wielokrotne zwiększenie/zmniejszenie.
Poprawka:
1 * – to działanie zachowujące stan
(- 1) * – to działanie zmieniające stan