Artykuł „Mnożenie liczb ujemnych – czyli dlaczego minus razy minus daje plus?” cieszy się ogromnym zainteresowaniem (np. w piątek 21.10.2016 został pobity rekord, mianowicie tylko w tym jednym dniu 350 unikalnych użytkowników zapoznało się z treścią wpisu). Będąc świadomym, że dla wielu z Was ważne jest zrozumienie motywacji stojącej za podstawowymi definicjami, postanowiłem rozpocząć nowy cykl „Dlaczego?”. Nowa seria skupi się na powszechnie znanych zagadnieniach, których wyjaśnienie nie jest już takie oczywiste. 🙂 Dziś na tapet idzie zero silnia! Przedstawię kilka argumentacji – w tym coś dla mniej i coś dla bardziej zaawansowanych! Będzie hardcorowo 🙂

Silnia – definicja

W celu przypomnienia

$$n!=n\times (n-1)\times (n-2)\times \ldots \times 2\times 1$$

Przykłady

$$4!=4\cdot 3\cdot 2\cdot 1=24$$

$$3!=3\cdot 2\cdot 1=6$$

$$2!=2\cdot 1=2$$

$$1!=1$$

$0!=???$ – no właśnie 🙂 – do tego wrócę za chwilkę!

Silnia jako liczba permutacji

W uproszczeniu permutacja zbioru (mówimy o zbiorach skończonych) to funkcja wyznaczająca kolejność jego elementów. Np. (1,2,3,4), (2,4,1,3), (4,3,2,1) … są różnymi permutacjami zbioru {1,2,3,4}.

W ogólnym przypadku – jeśli mamy do czynienia ze zbiorem n-elementowym otrzymujemy:

• n sposobów wyboru elementu 1 (bo mamy do dyspozycji cały zbiór)
• n-1 sposobów wyboru elementu 2 (bo pierwszy jest już wybrany, pozostało n-1)
• n-2 sposobów wyboru elementu 3 (bo 2 pierwsze są już wybrane, pozostało n-2)
• …
• n-(k-1) sposobów wyboru elementu k (bo k-1 pierwszych jest już wybranych, pozostało n-(k-1) )
• …
• 2 sposoby wyboru elementu n-1 (bo n-2 elementy wybrano, pozostały wolne 2)
• 1 sposób wyboru elementu n (bo n-1 elementów wybrano, pozostał wolny tylko 1)

i finalnie liczba różnych uporządkowań zbioru n-elementowego wynosi:

$${\small n\times (n-1)\times (n-2)\times \ldots \times 2\times 1=n!}$$

Zatem interpretacja n! to liczba permutacji (czyli liczba różnych uporządkowań) zbioru n-elementowego.

No dobrze – ale jak to pomaga w ustaleniu 0! (zero silnia)? Przecież ciężko mówić o kolejności elementów zbioru pustego… Do tego wrócę również nieco później 🙂

Wariacja bez powtórzeń

Brrr – paskudna ta nazwa – ale ok – spróbujmy. Mówimy, że wybór dokładnie k-różnych elementów, zwracając uwagę na kolejność, ze zbioru n-elementowego, jest k-elementową wariacją bez powtórzeń zbioru n-elementowego. Przykłady różnych 3-elementowych wariacji bez powtórzeń zbioru {1,2,3,4,5} to: (1,2,3), (3,2,1),(4,5,2),…

Liczbę $V_n^k$ k-elementowych wariacji bez powtórzeń zbioru n-elementowego wyznaczymy na bazie:

• n sposobów wyboru elementu 1
• n-1 sposobów wyboru elementu 2
• n-2 sposobów wyboru elementu 3
• …
• n-(k-1) sposobów wyboru elementu k

i finalnie

$${\large V_n^k}={\small n\times (n-1)\times (n-2)\times\ldots\times \bigg(n-(k-1)\bigg)}$$

ale

$${\small n\times (n-1)\times (n-2)\times \ldots\times \big(n-(k-1)\big)}=…$$

$$={\small\frac{n\times (n-1)\times (n-2)\times \ldots\times \big(n-(k-1)\big)\times (n-k)\times \ldots \times 2\times 1}{(n-k)\times \ldots \times 2\times 1}}=…$$

$$…=\frac{n!}{(n-k)!}$$

Zatem

$${\large V_n^k=}{\Large\frac{n!}{(n-k)!} }$$

0! = 1 (słownie: zero silnia równa się jeden)

Zauważmy, że n-elementowa wariacja bez powtórzeń zbioru n-elementowego jest w zasadzie jego permutacją, zatem liczba takich wariacji będzie równa liczbie permutacji, co zapisujemy:

$${\large V_n^n=n!}$$

ale

$${\large V_n^n=}{\Large \frac{n!}{(n-n)!}}={\Large \frac{n!}{0!}}$$

w konsekwencji

$$n!={\large \frac{n!}{0!}}$$

$${0!\cdot n!=n!}$$

$${\Large 0!=1}$$

Powyższe uzasadnia, że przyjęcie 0!=1 jest wygodne, gdyż zapewnia „spójność” podstawowych wzorów. Ale czy stoi za tym coś więcej?

!!! Dalsza część dla nieco bardziej zaawansowanych czytelników !!!

Funkcja jako odwzorowanie zbiorów

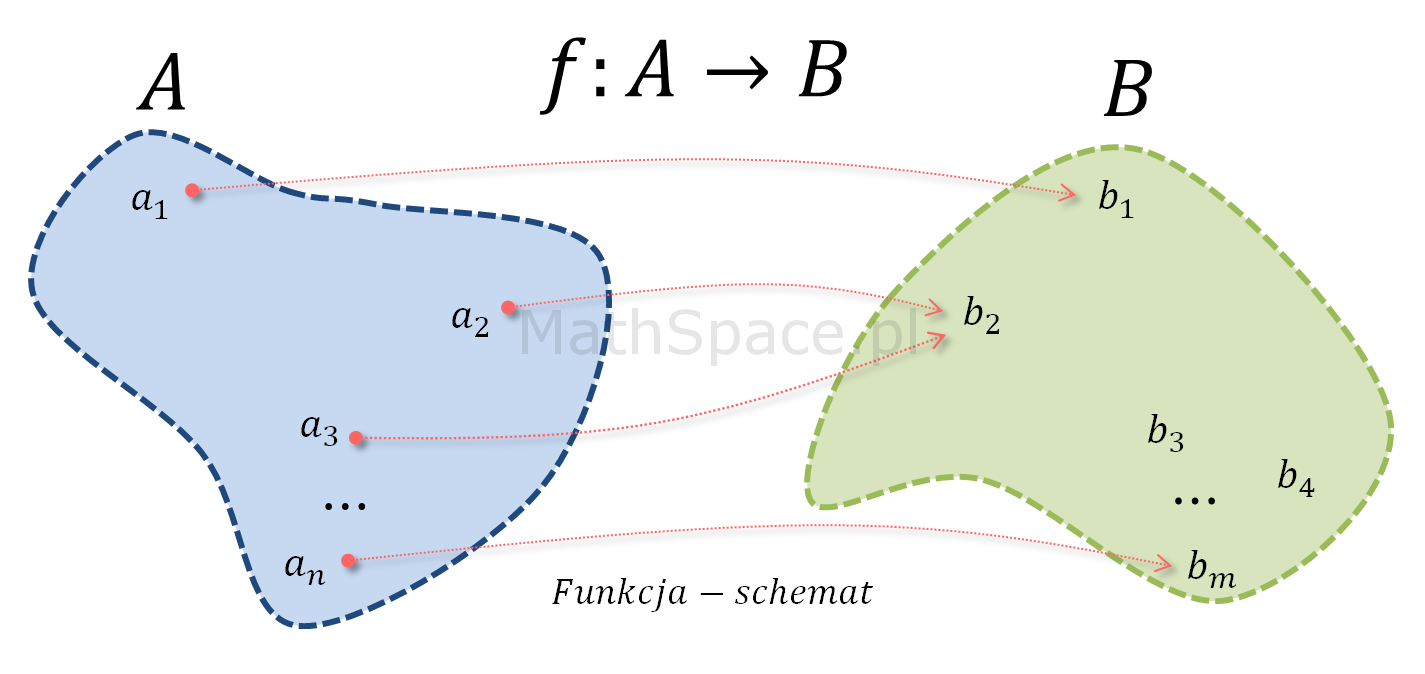
Funkcja $f:A\to B$, gdzie dla każdego $a \in A$ istnieje $f(a)=b\in B$ wyznacza tak naprawdę relację pomiędzy elementami $a$ i $b$. Przy takim podejściu możemy powiedzieć, że elementy $a\in A$ oraz $b\in B$ są w relacji $f$ wtedy i tylko wtedy gdy $f(a)=b$.

Funkcja jako podzbiór iloczynu kartezjańskiego

Funkcję $f:A\to B$ możemy potraktować jako podzbiór iloczynu kartezjańskiego zbiorów A i B, co symbolicznie zapiszemy $f\subseteq A\times B$

$$(a,b)\in f \subseteq A\times B \iff f(a)=b$$

Dobrym przykładem jest wykres funkcji rzeczywistej, który jest podzbiorem płaszczyzny.

Iniekcja – czyli funkcja różnowartościowa

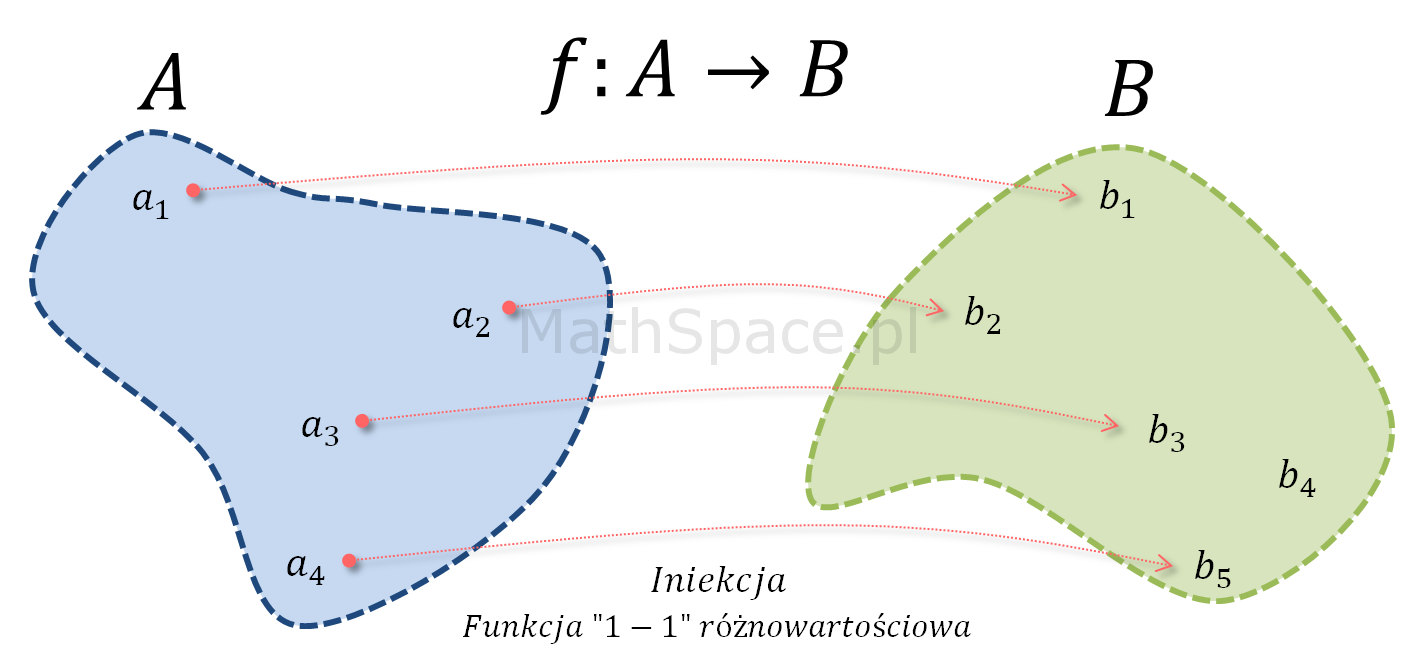
Iniekcja to inaczej funkcja różnowartościowa, tzn. funkcja $f:A\to B$ jest różnowartościowa wtedy i tylko wtedy, gdy dla dowolnych elementów $x,y\in A$ spełniony jest warunek

$$x\neq y \implies f(x) \neq f(y)$$

Surjekcja – czyli funkcja „na”

Surjekcja to taki przypadek funkcji $f:A\to B$, że każdy element zbioru B ma swój odpowiednik w zbiorze A. Formalnie zapiszemy to tak

$${\large \displaystyle\forall_{b \in B} \quad\displaystyle\exists_{a\in A}\quad}f(a)=b$$

Bijekcja – czyli funkcja odwracalna (wzajemnie jednoznaczna)

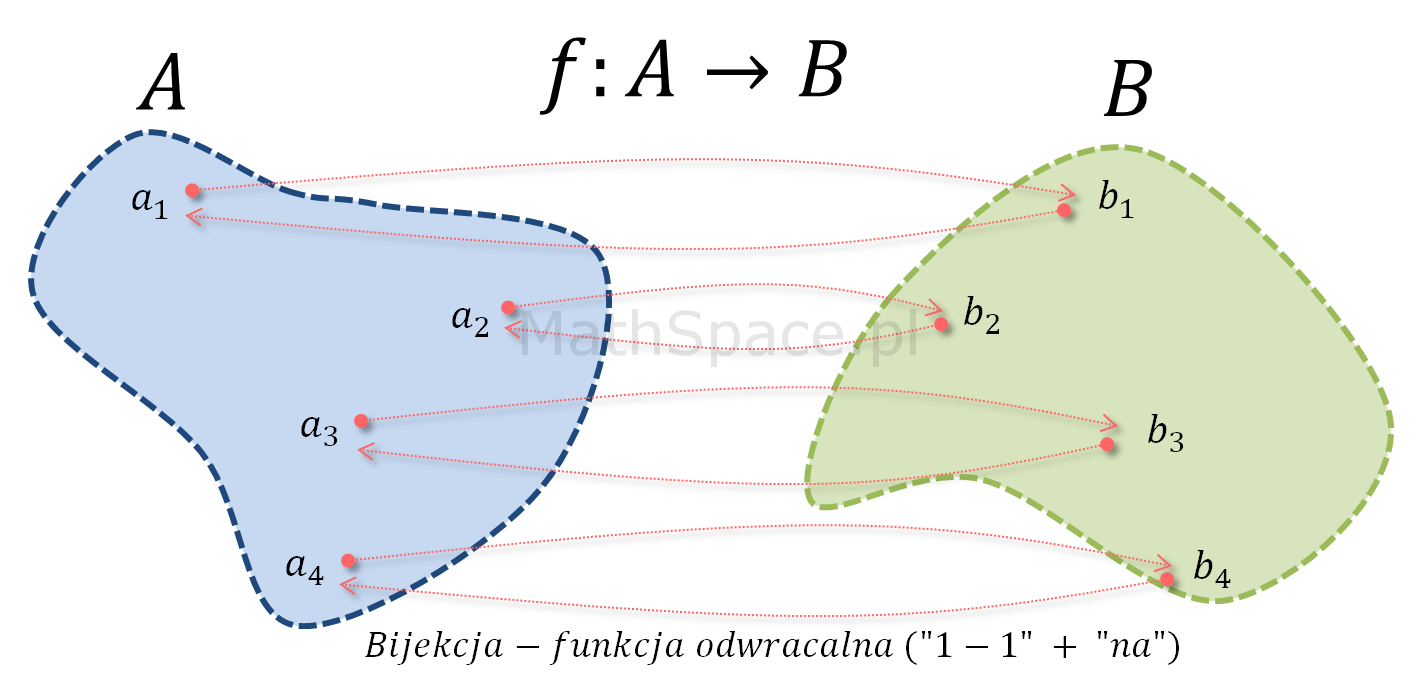
Bijekcja to funkcja $f:A\to B$, która jednocześnie spełnia warunek iniekcji oraz surjekcji, tzn. jest różnowartościowa oraz „na”. Bijekcja jest funkcją odwracalną i wyznacza odwzorowanie wzajemnie jednoznaczne zbioru A na zbiór B (każdy element zbioru A jest jednoznacznie przypisany do elementu zbioru B, oraz każdy element zbioru B ma jednoznaczny odpowiednik w zbiorze A).

Bijekcja vs Permutacja

Permutacja jest funkcją zwracająca uporządkowanie zbioru, tzn. jeśli rozważamy n-elementowy zbiór {1, 2, …, n} to permutacja będzie funkcją

$$p:\{1, 2, …, n\}\to\{1, 2, …, n\}$$

spełniającą warunek bijekcji. Pytając o liczbę permutacji możemy równoważnie pytać o liczbę różnych bijekcji z danego zbioru w samego siebie.

Funkcja pusta $f:\emptyset\to B$

Funkcją pustą nazywamy każdą funkcję, której dziedziną jest zbiór pusty.

$$f:\emptyset\to B$$

Wykres funkcji pustej jest zbiorem pustym, gdyż iloczyn kartezjański $\emptyset\times B=\emptyset$. Funkcja pusta jest różnowartościowa, gdyż w dziedzinie (czyli w zbiorze pustym) nie istnieją takie dwa różne elementy, dla których wartość funkcji jest równa.

Funkcja pusta $f:\emptyset\to \emptyset$

Funkcja pusta $f:\emptyset\to \emptyset$ jest bijekcją, gdyż nie istnieje element przeciwdziedziny (przeciwdziedzina jest zbiorem pustym) nie będący w relacji z elementem dziedziny. Zauważmy, że istnieje dokładnie jedna bijekcja $f:\emptyset\to \emptyset$ co wynika z faktu, że funkcja jest podzbiorem iloczynu kartezjańskiego dziedziny i przeciwdziedziny. W przypadku rozważanej funkcji pustej $f:\emptyset\to \emptyset$ wspominany iloczyn kartezjański to zbiór pusty $\emptyset\times\emptyset=\emptyset$, który ma dokładnie jeden podzbiór – również zbiór pusty.

0! = 1 vs funkcja pusta $f:\emptyset\to \emptyset$

Pisałem wyżej, że liczbę permutacji zbioru n-elementowego można utożsamiać z liczbą bijekcji z tego zbioru w samego siebie. Tym samym permutacjom zbioru 0-elementowego odpowiadają bijekcje ze zbioru pustego w zbiór pusty – a taka funkcja jest dokładnie jedna! 🙂 Trochę abstrakcyjne, ale się zgadza 🙂

Funkcja Gamma (zwana również gammą Eulera) – czyli silnia dla liczb rzeczywistych i zespolonych

Funkcja Gamma jest funkcją, która rozszerza pojęcie silni na cały zbiór liczb rzeczywistych, a nawet zespolonych!

$$\Gamma(z)=\displaystyle\int_0^{+\infty}t^{z-1}e^{-t}dt$$

 Okazuje się (po scałkowaniu przez części), że

$$\Gamma(z+1)=z\cdot\Gamma(z)$$

oraz

$$\Gamma(1)=\displaystyle\int_0^{+\infty}e^{-t}dt=…$$

$$…=\displaystyle\int_{-\infty}^{0}e^{t}dt=…$$

$$…=[e^{t}]_{-\infty}^{0}=…$$

$$…=e^0-e^{-\infty}=1-0=1$$

 $$\Gamma(1)=1$$

Z powyższego wynika, że dla wszystkich całkowitych liczb $n\geq 0$ zachodzi

 $${\Gamma(n+1)=n!}$$

 $${\large0!=\Gamma(1)=1}$$

Kolejne bardzo ciekawe spostrzeżenie, że ${0!}$ ma związek z funkcją eksponencjalną!!

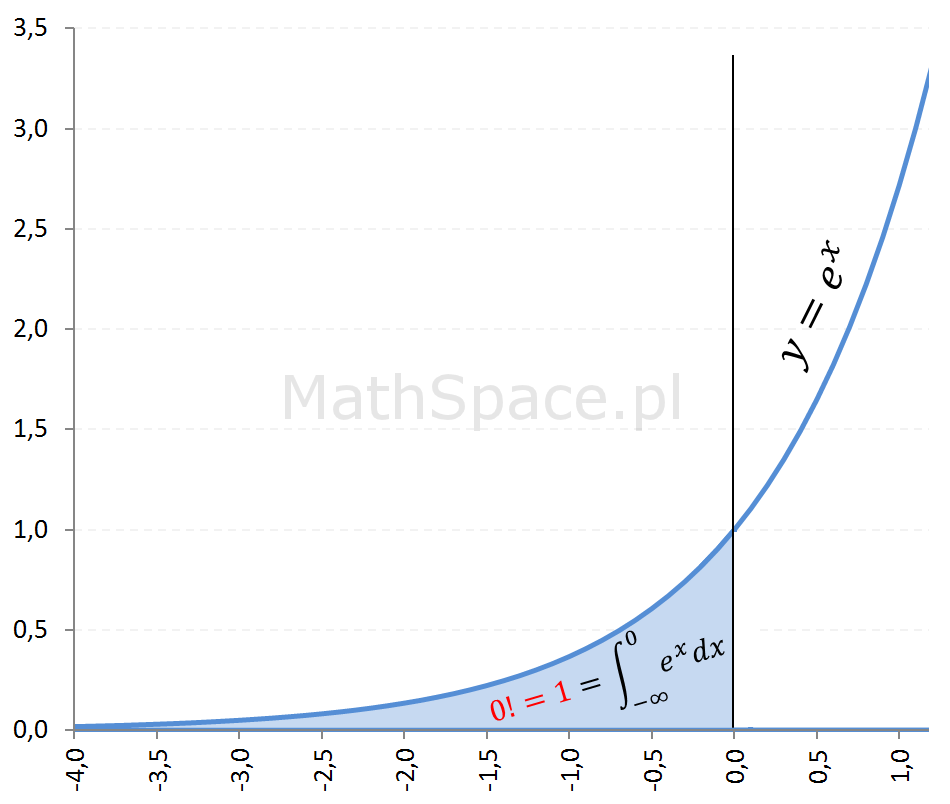
Zwięzek liczby e oraz silni jest nawet większy!

$$e=\displaystyle\sum_{n=0}^\infty\frac{1}{n!}=\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\ldots$$

Obiecałem, że będzie hardcorowo – i było 🙂

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa