Artykuł „Mnożenie liczb ujemnych – czyli dlaczego minus razy minus daje plus?” cieszy się ogromnym zainteresowaniem (np. w piątek 21.10.2016 został pobity rekord, mianowicie tylko w tym jednym dniu 350 unikalnych użytkowników zapoznało się z treścią wpisu). Będąc świadomym, że dla wielu z Was ważne jest zrozumienie motywacji stojącej za podstawowymi definicjami, postanowiłem rozpocząć nowy cykl „Dlaczego?”. Nowa seria skupi się na powszechnie znanych zagadnieniach, których wyjaśnienie nie jest już takie oczywiste. 🙂 Dziś na tapet idzie zero silnia! Przedstawię kilka argumentacji – w tym coś dla mniej i coś dla bardziej zaawansowanych! Będzie hardcorowo 🙂
Miesiąc: październik 2016
Pierwsze urodziny MathSpace.pl

Pierwszy wpis pojawił się 20 października 2015.
Przez rok opublikowałem 57 artykułów, znaczna część zamieszczona w 6 seriach:
- Ocena jakości klasyfikacji – 8 części
- Geometria fraktalna – 2 części
- Spirala Ulama – 2 części
- Zabawy z rekurencją – 5 części
- Liczby zespolone – 1 część
- Matematyka w obrazkach – 10 części
Każdego dnia blog odwiedza około 40-50 osób – to niezły wynik zważywszy na raczej niełatwą tematykę 🙂
Google docenił MathSpace.pl, w efekcie dla szeregu zapytań blog pozycjonowany jest bardzo wysoko.
Dziękuję! 🙂
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa
Karl Weierstrass i Funkcja Weierstrassa – czyli geometria fraktalna (część 2)

Karl Theodor Wilhelm Weierstrass (1815 – 1897) niemiecki matematyk uznawany za „ojca współczesnej analizy matematycznej”. Choć minęło już 17 lat, to nadal doskonale pamiętam pierwszy semestr studiów matematycznych i ekspozycję na podstawowe „bardziej abstrakcyjne” twierdzenia, w tym Twierdzenie Bolzano-Weierstrassa. Twierdzenie mówi, że „każdy rzeczywisty ciąg ograniczony zawiera podciąg zbieżny”, i choć brzmi prosto i ogólnie, jest niezwykle przydatnym narzędziem dowodzenia innych wyników metodą nie-wprost (zgodnie ze schematem „załóżmy, że … wtedy istnieje ciąg ograniczony, że …, wtedy istnieje podciąg zbieżny, że …, i z własności … wynika sprzeczność z założeniem”). Pięknie to (i nie tylko to) wykładał Pan Prof. Dr Hab. Tadeusz Rzeżuchowski – wielkie dzięki Panie Profesorze!
Funkcja Weierstrassa
Większość matematyków z okresu XVIII i XIX wieku uważało, że wszystkie rzeczywiste funkcje ciągłe są różniczkowalne w znaczącej części swej dziedziny (poza zbiorem izolowanych punktów). Dosyć naturalny pogląd okazał się jednak fałszywy, co wykazał Weierstrass w 1872 roku, a wcześniej podejrzewali Bernhard Riemann oraz Bernard Bolzano (prawdopodobnie w roku 1830 Bolzano podał kontrprzykład, którego nie opublikował). Funkcja Weierstrassa jest przykładem rzeczywistej funkcji ciągłej nieróżniczkowalnej w całej dziedzinie (tzn. nie istnieje ani jeden punkt dziedziny, w otoczeniu którego funkcja zachowuje się „normalnie” – np. monotonicznie). Własność nietypowa, a nawet patologiczna! Jednak nie dla fraktali, zatem i nie dla otaczającej nas natury (analogia do nieintuicyjnej mechaniki kwantowej zaskakująco precyzyjnie opisującej rzeczywistość).
$${\Large f(x)=\displaystyle\sum_{n=0}^\infty a^n\cos(b^n\pi x)}$$
gdzie
$${\large 0<a<1\qquad ab>1+\frac{3}{2}\pi}$$
Warto zauważyć, że funkcję Weierstrassa można zapisać w postaci analitycznej (w uproszczeniu – podając wzór).
Funkcja Weierstrassa i fraktale
Poniżej wykres funkcji Weierstrassa na przedziale [-2; 2] – źródło Wikipedia.
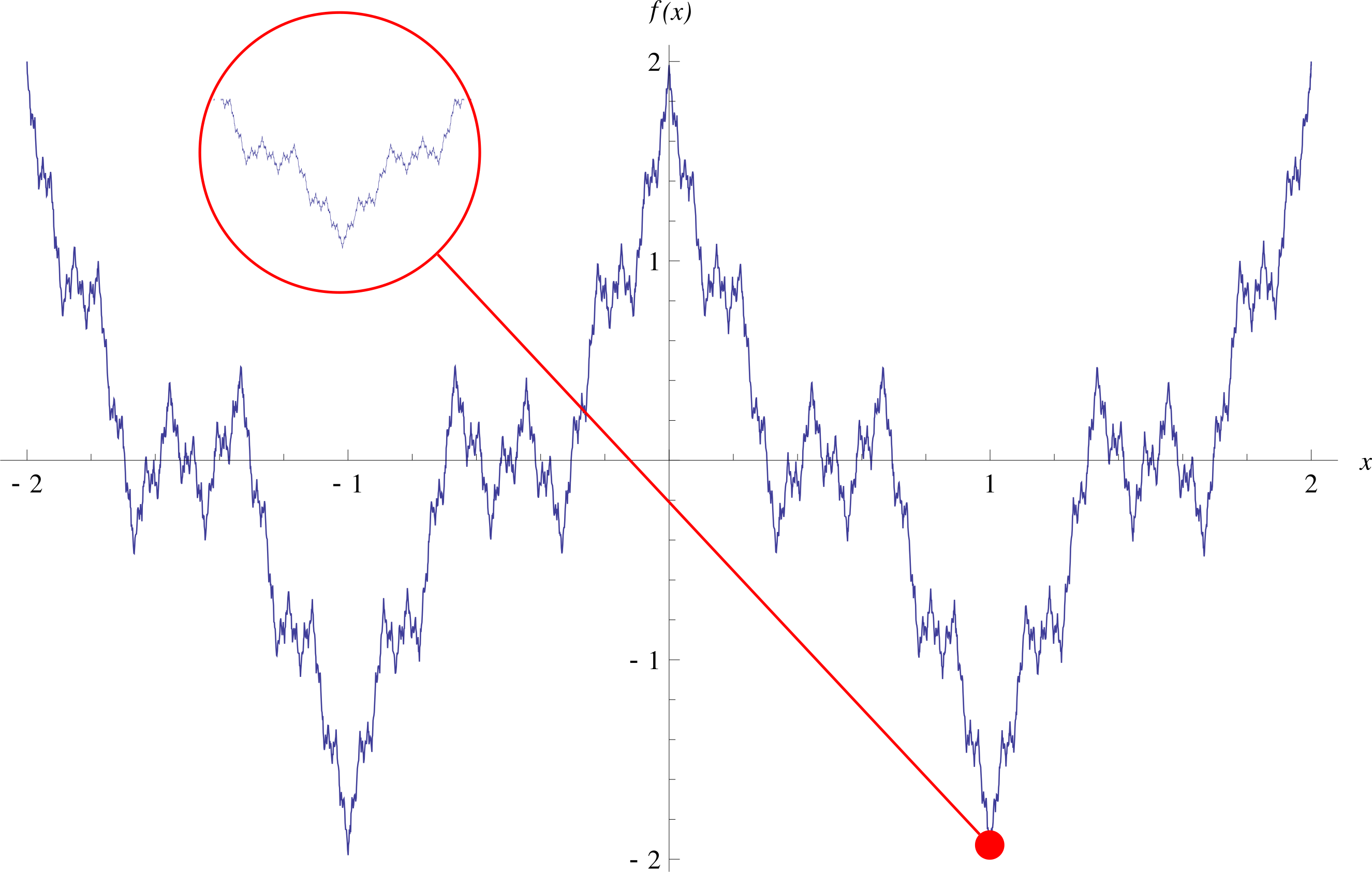
Benoit Mandelbrot mawiał, że „fraktal to zbiór matematyczny (lub inny obiekt ) charakteryzujący się w każdej skali wysoką nieregularnością oraz dużą fragmentacją.” W części pierwszej cyklu o „geometrii fraktalnej”, odnosząc się do słów Mandelbrota, pisałem, że cechą fraktalną jest nietrywialna struktura obiektu w każdej skali – tzn. powiększanie ujawnia kolejne równie skomplikowane formy. Wspomniałem również o samo-podobieństwie – tzn. sytuacji, gdy w skład obiektu wchodzą jego „mniejsze” kopie. Wykres funkcji Weierstrassa zdaje się spełniać te kryteria – był to pierwszy odkryty fraktal!
Karl Weierstrass – ciekawostki
Weierstrass wykładał w Wałczu oraz w Braniewie. Wikipedia wymienia, że jego uczniami byli: Georg Cantor, Otto Holder, Georg Frobenius, Felix Klein, Hermann Minkowski.
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa
Captured Response = ROC x apriori – czyli ocena jakości klasyfikacji (część 8)
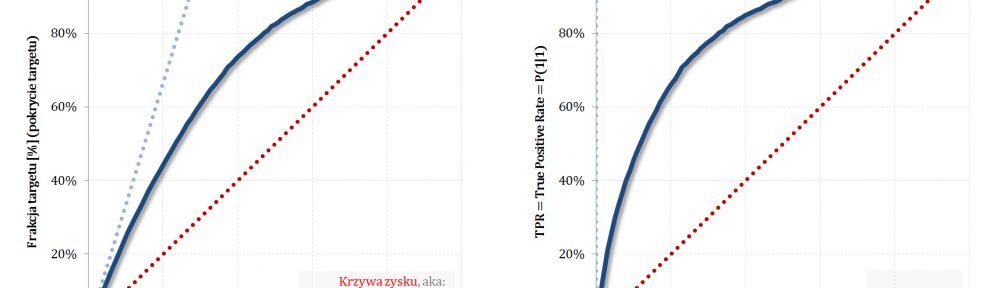
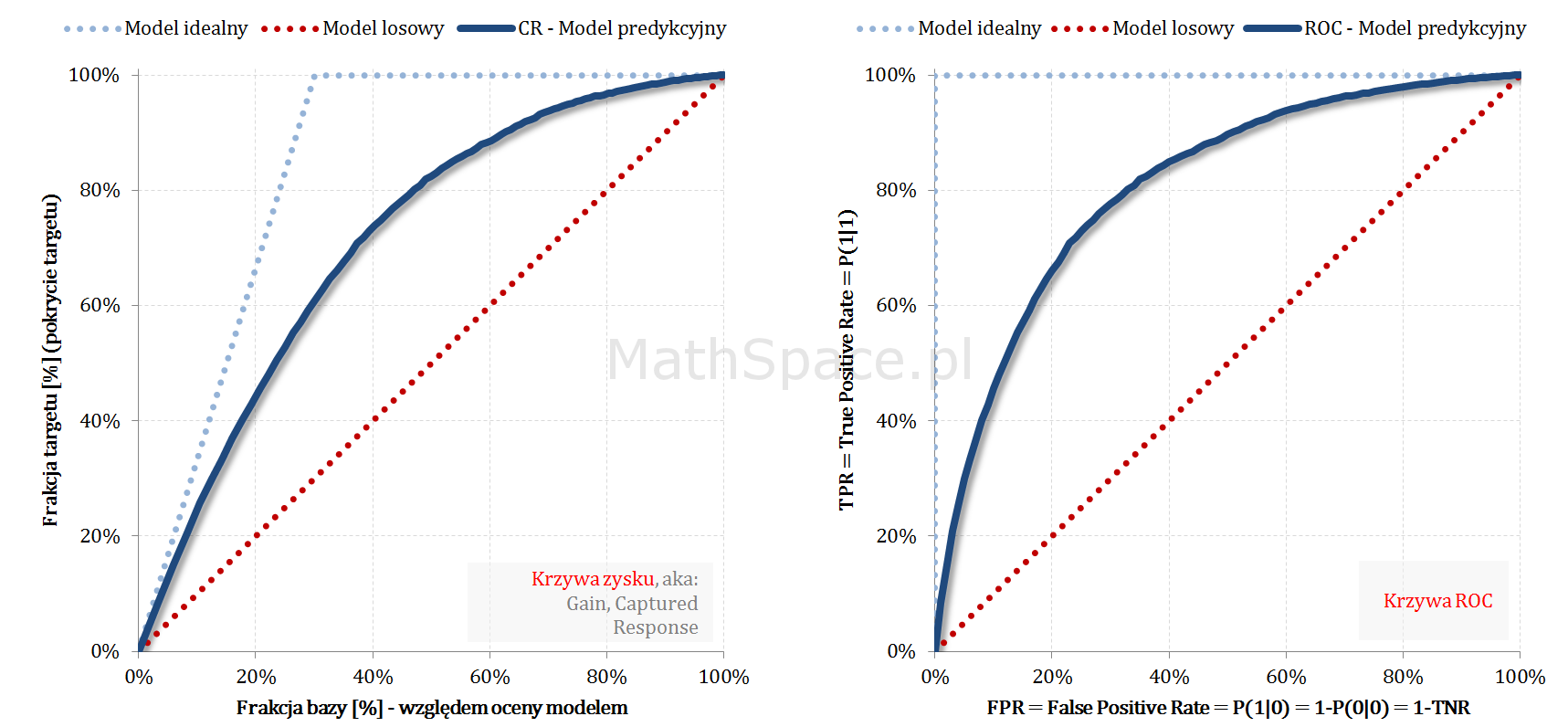
W części #6 oraz części #7 cyklu „Ocena jakości klasyfikacji” przedstawiłem krzywą zysku (aka: Gain, Captured Response) oraz krzywą ROC. Dzisiaj skupię się na mało znanej, acz bardzo prostej i przydatnej, relacji pomiędzy tymi krzywymi – okazuje się bowiem, że wykresy są „niemal identyczne” 🙂
Wzór łączący ROC z Captured Response
$$X_{cr}=Y_{roc}\times apriori+X_{roc}\times \Big(1-apriori\Big)$$
$$Y_{cr}=Y_{roc}$$
Geometryczne podobieństwo Captured Response i ROC
Odpowiednio spoglądając na umieszczone obok siebie wykresy ciężko odeprzeć wrażenie, że krzywe są bardzo podobne. Intuicja podpowiada, że mamy tu do czynienia z tymi samymi funkcjami, jedynie naszkicowanymi w nieco różnych układach współrzędnych.
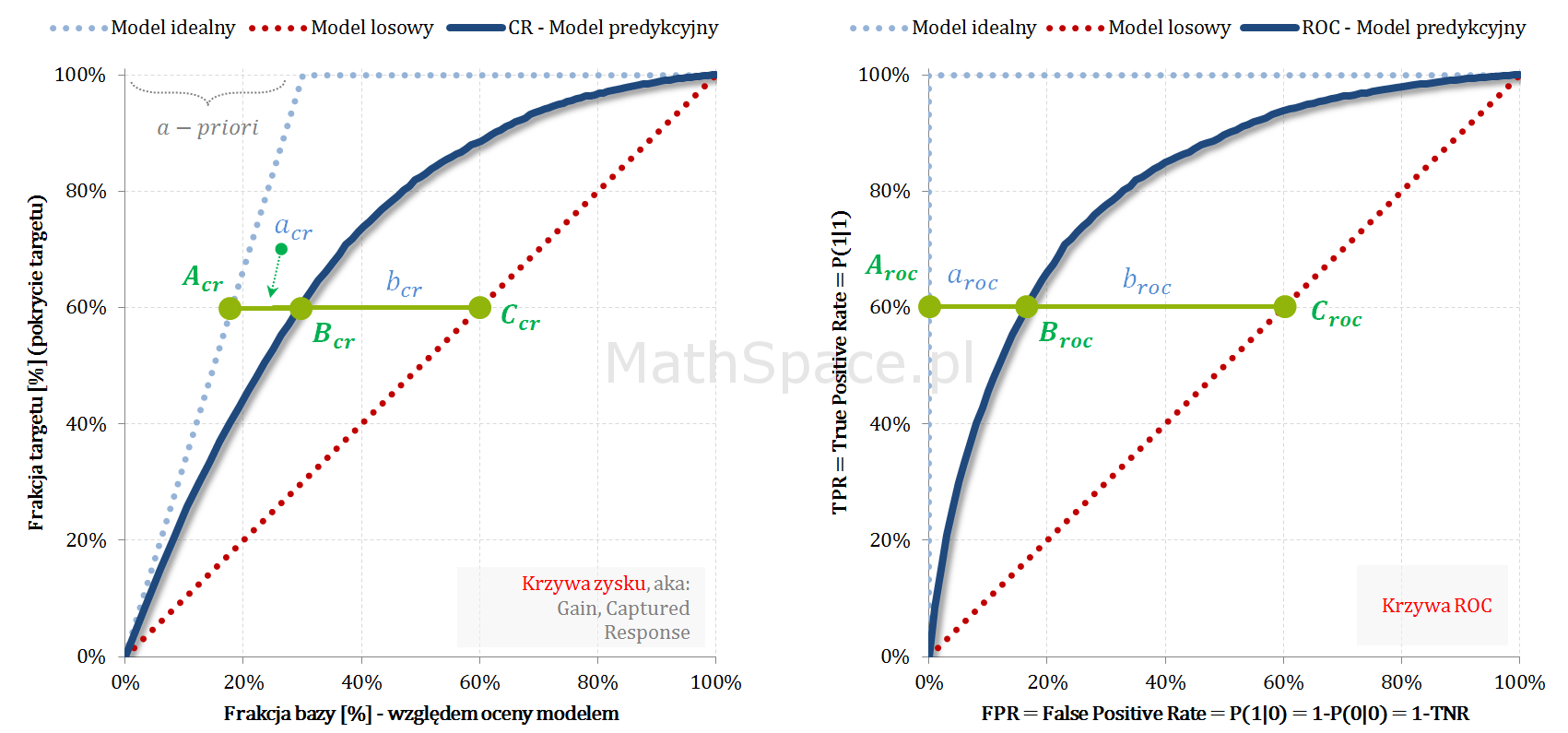
W obu przypadkach to „przestrzeń” pomiędzy modelem losowym i modelem idealnym definiuje odpowiedni układ współrzędnych, a różnica obecna w Captured Response powiązana jest z a-priori (CR jest zależna od a-priori, ROC nie zależy od a-priori). Idąc za kolejnym przeczuciem powiemy, że najprawdopodobniej dla tej samej wartości „Y” różnić się będą wartości „X” (ze względu na „ściśniecie” obecne w Captured Response).
Wzór na bazie macierzy przekształcenia liniowego – jedynie poglądowo
Uwaga: poniższe wyprowadzenie jest jedynie pomocnicze, nie stanowi wystarczającej argumentacji uzasadniającej „identyczność” krzywych Captured Response i ROC!!! Formalna argumentacja znajduje się w kolejnej sekcji.

Zauważmy, że wektor
$\begin{bmatrix}X_{ROC}=0\\Y_{ROC}=1\end{bmatrix}$ przechodzi w $\begin{bmatrix}X_{CR}=apriori\\Y_{CR}=1\end{bmatrix}$
oraz wektor
$\begin{bmatrix}X_{ROC}=1\\Y_{ROC}=1\end{bmatrix}$ przechodzi w $\begin{bmatrix}X_{CR}=1\\Y_{CR}=1\end{bmatrix}$
Zatem macierz przekształcenia liniowego przyjmuje postać (potrzeba rozwiązać prościutki układ równań):
$$A=\begin{bmatrix}1-apriori & apriori\\0 & 1\end{bmatrix}$$
Finalne przekształcenie ROC w Capture Response to:
$$\begin{bmatrix}1-apriori & apriori\\0 & 1\end{bmatrix}\times\begin{bmatrix}X_{ROC}\\Y_{ROC}\end{bmatrix}=\begin{bmatrix}X_{CR}\\Y_{CR}\end{bmatrix}$$
Wynik bardzo ciekawy – faktycznie wystarczy a-priori 🙂 Jednak to nie jest dowód, wyprowadzenie bazowało na intuicji …
Wzór na bazie proporcji – jedynie poglądowo
Uwaga: Ponownie – poniższe wyprowadzenie jest jedynie pomocnicze, nie stanowi wystarczającej argumentacji uzasadniającej „identyczność” krzywych Captured Response i ROC!!! Formalna argumentacja znajduje się w kolejnej sekcji.
Oznaczmy punkty (wykres powyżej):
$B_{cr}=\Big(X_{cr}, Y_{cr}\Big)$ – punkt na krzywej Captured Response
$B_{roc}=\Big(X_{roc}, Y_{roc}\Big)$ – punkt na krzywej ROC
Podążając za „głosem wewnętrznym” 🙂 napiszemy równość
$$Y_{cr}=Y_{roc}$$
oraz równość proporcji długości odcinków
$${\Large\frac{a_{cr}}{a_{cr}+b_{cr}}=\frac{a_{roc}}{a_{roc}+b_{roc}}}$$
To pozwoli wyprowadzić formułę dla wartość $X_{cr}$ w zależności od współrzędnych $\Big(X_{roc}, Y_{roc}\Big)$.
Długość odcinka: $a_{roc}=X_{roc}$
Długość odcinka: $a_{roc}+b_{roc}=Y_{roc}$ (wynika z pozycji punktu $C_{roc}=C_{cr}$).
Przechodzimy od wyznaczenia współrzędnych punktu $A_{cr}$ leżącego na krzywej idealnej wykresu Capture Response.
Prosta „idealna” jest opisana równaniem: $y={\Large\frac{x}{apriori}}$ dla x mniejszych od a-priori, zatem
$$x=y\times apriori$$
I dalej współrzędne
$$A_{cr}=\Big(Y_{cr}\times apriori, Y_{cr}\Big)=\Big(Y_{roc}\times apriori, Y_{roc}\Big)$$
Zaś współrzędne
$$B_{cr}=\Big(X_{cr}, Y_{cr}\Big)=\Big(X_{cr}, Y_{roc}\Big)$$
$$C_{cr}=\Big(Y_{cr}, Y_{cr}\Big)=\Big(Y_{roc}, Y_{roc}\Big)$$
W tej chwili przystępujemy do wyznaczenia długości odcinków
Długość odcinka: $a_{cr}=X_{cr}-Y_{roc}\times apriori$
Długość odcinka: $a_{cr}+b_{cr}=Y_{roc}-Y_{roc}\times apriori=Y_{roc}\Big(1-apriori\Big)$
Kilka ostatnich kroków
$${\Large\frac{a_{cr}}{a_{cr}+b_{cr}}=\frac{a_{roc}}{a_{roc}+b_{roc}}}$$
$${\Large\frac{X_{cr}-Y_{roc}\times apriori}{Y_{roc}\Big(1-apriori\Big)}=\frac{X_{roc}}{Y_{roc}}}$$
Mnożymy przez $Y_{roc}$
$${\Large\frac{X_{cr}-Y_{roc}\times apriori}{1-aprior}}=X_{roc}$$
$$X_{cr}-Y_{roc}\times apriori=X_{roc}\times \Big(1-apriori\Big)$$
I finalnie
$$X_{cr}=Y_{roc}\times apriori+X_{roc}\times \Big(1-apriori\Big)$$
$$Y_{cr}=Y_{roc}$$
Wynik identyczny – jednak to nadal nie dowód …
Pełny dowód na bazie macierzy błędu i prawdopodobieństw
Oś „Y” w przypadku ROC to True-Positive Rate, czyli
$$TPR={\Large\frac{TP}{TP+FN}}={\Large\frac{TP}{Faktyczne.P}}=P(1|1)$$
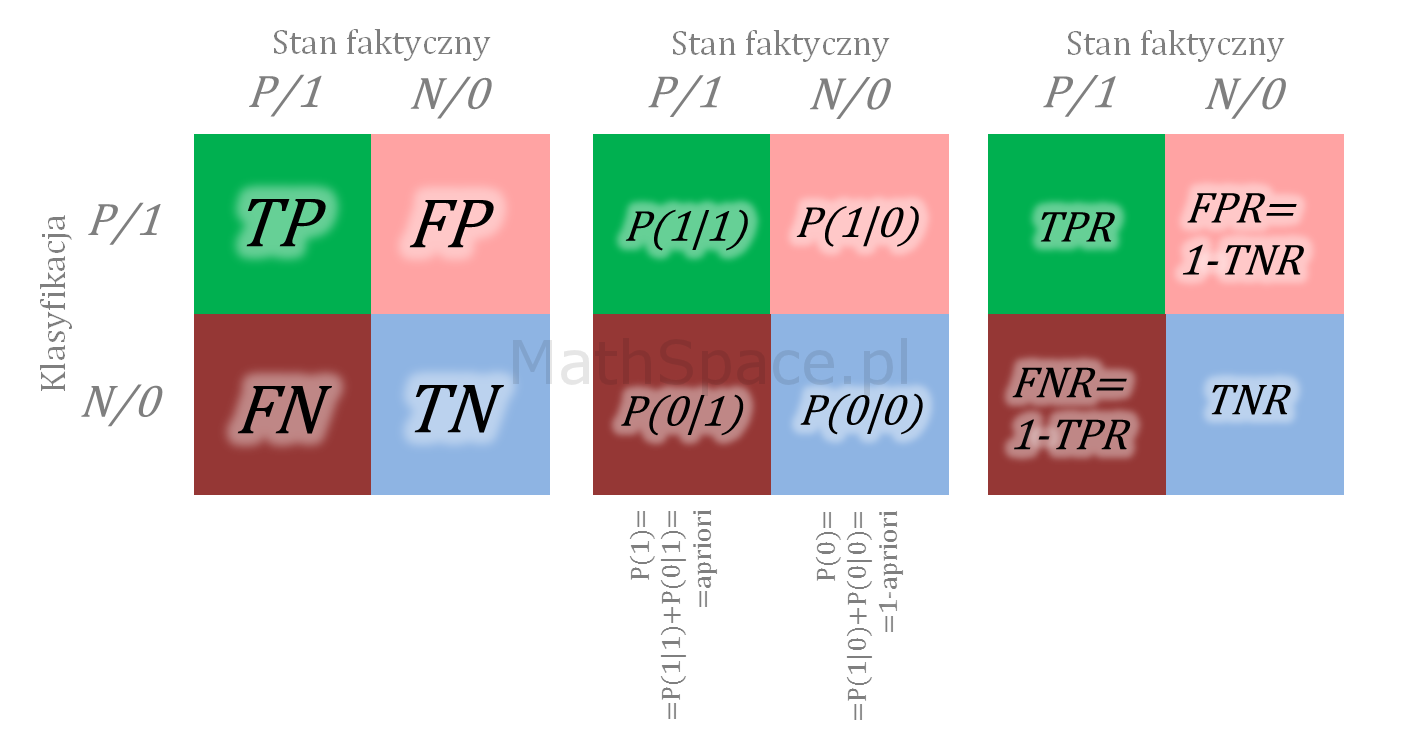
Z powyższego bezpośrednio wynika, że
$$Y_{cr}=Y_{roc}$$
Współrzędna „X” krzywej Captured Response to kwantyl bazy, tzn. gdyby założyć, że X% bazy klasyfikujemy pozytywnie, to dotrzemy do Y% frakcji targetu – zatem $X_{cr}$ jest rozmiarem frakcji przewidywania pozytywnego. Rozważmy poniższy rozkład oceny modelem.
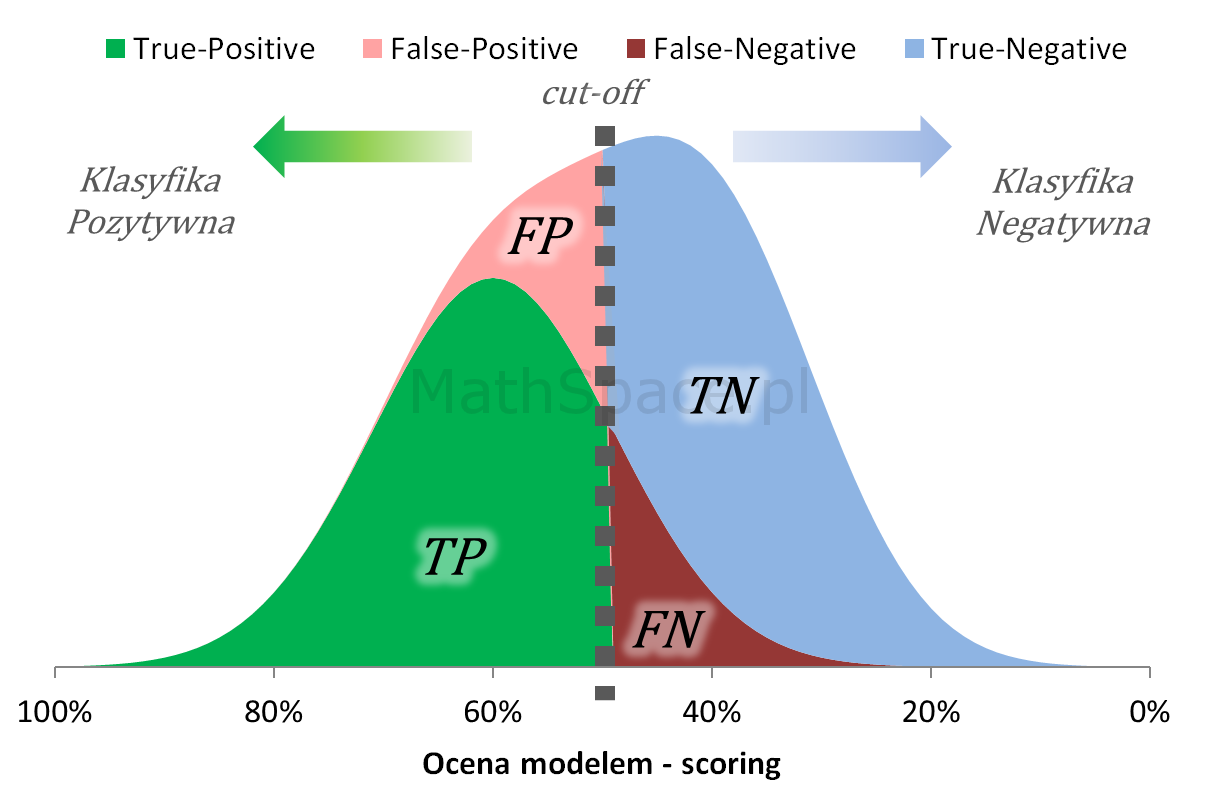
Przewidywanie pozytywne składa się z frakcji TP+FP, ale
$$Klasyf.P=TP+FP=…$$
$$…=TPR\times Faktyczne.P+FPR\times Faktyczne.N$$
$$P(klasyf=P)=…$$
$$…=TPR\times apriori+FPR\times (1-apriori)=…$$
$$…=P(1|1)P(1)+P(1|0)P(0)$$
Finalnie
$$X_{cr}=Y_{roc}\times apriori+X_{roc}\times \Big(1-apriori\Big)$$
$$Y_{cr}=Y_{roc}$$
Co z tego wynika?
- Rozumiejąc relację pomiędzy krzywą ROC a krzywą Captured Response analiza modelu jest znacznie prostsza, szczególnie jeśli korzystamy z narzędzia, które prezentuje tylko jeden wariant krzywej (często ROC). Przy małych apriori oś „X” krzywej ROC można praktycznie uznać za oś „X” krzywej Captured Response. Przy większych apriori należy intuicyjnie przesuwać „X” w prawo aby z ROC uzyskać Captured Response.
- Gini policzone na ROC oraz na CR (pamiętając o przestrzeni pomiędzy modelem losowym i modelem idealnym) bedą sobie równe.
Przykład działania wzoru
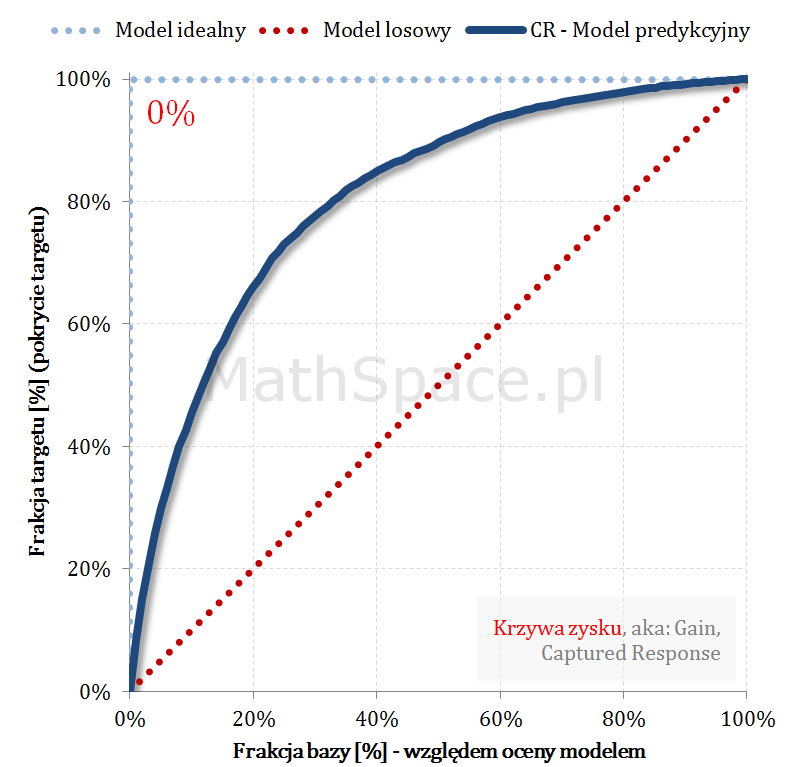
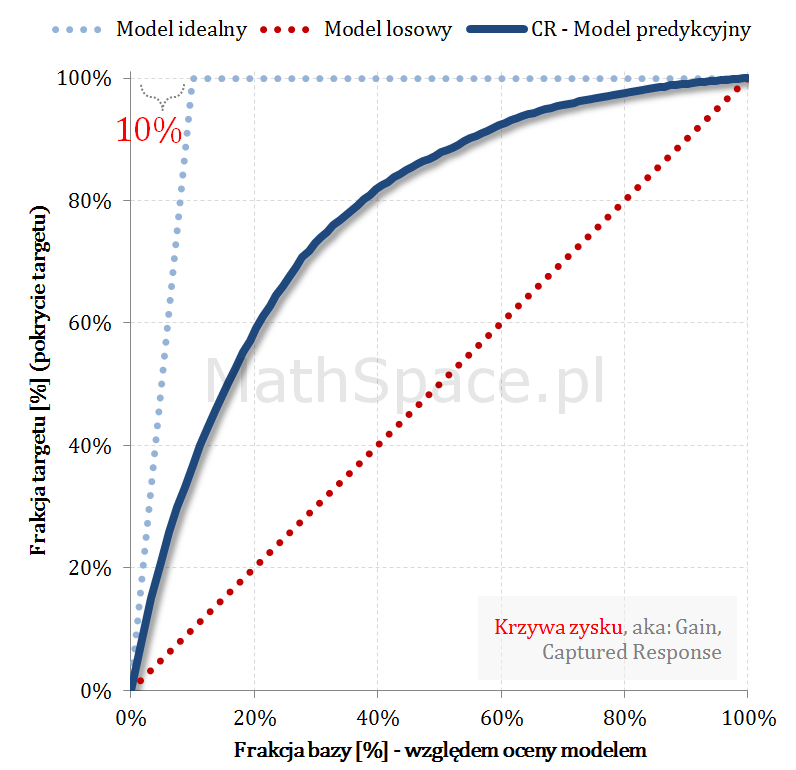
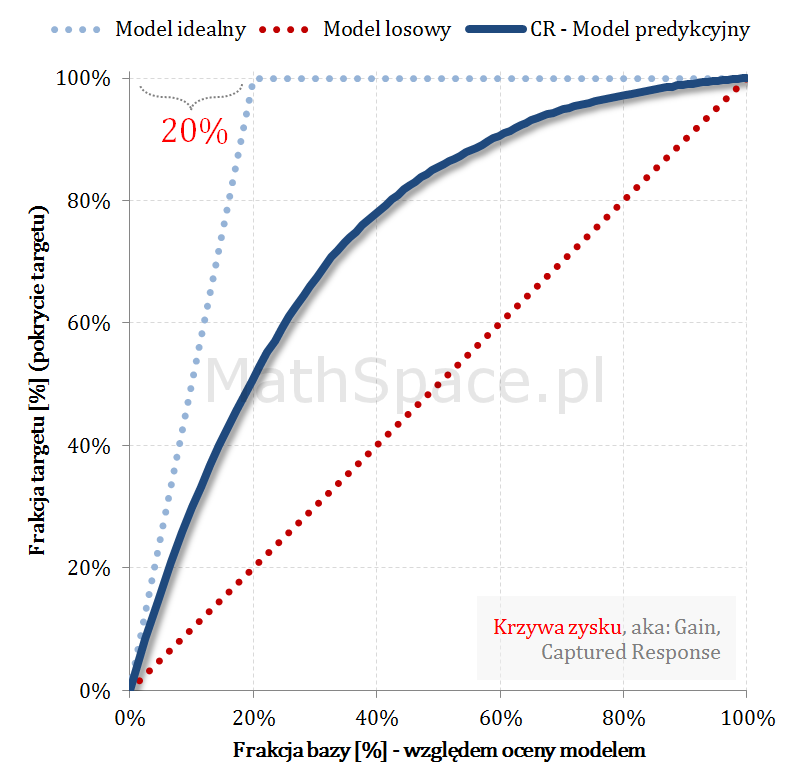
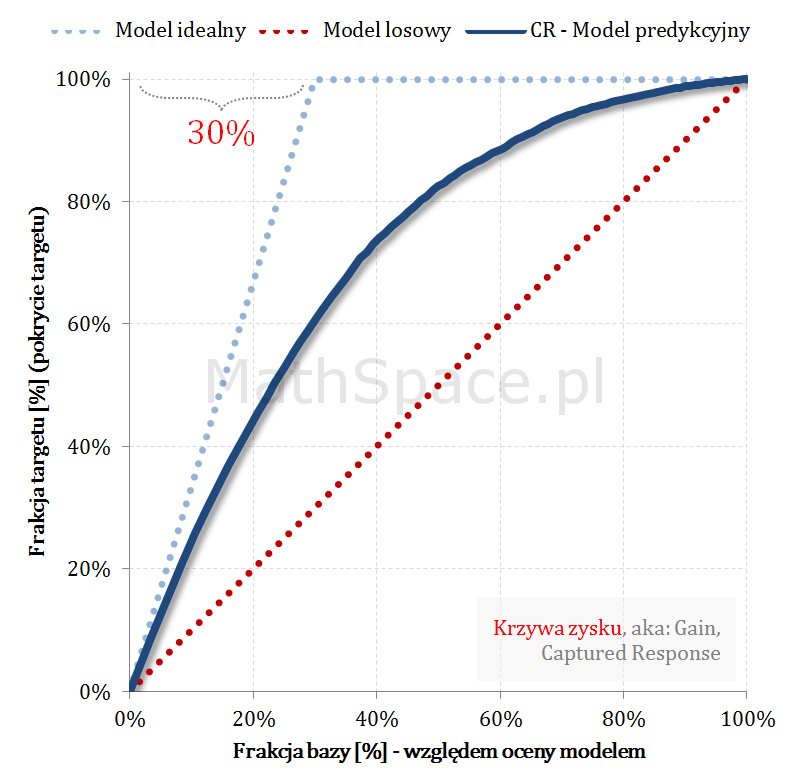
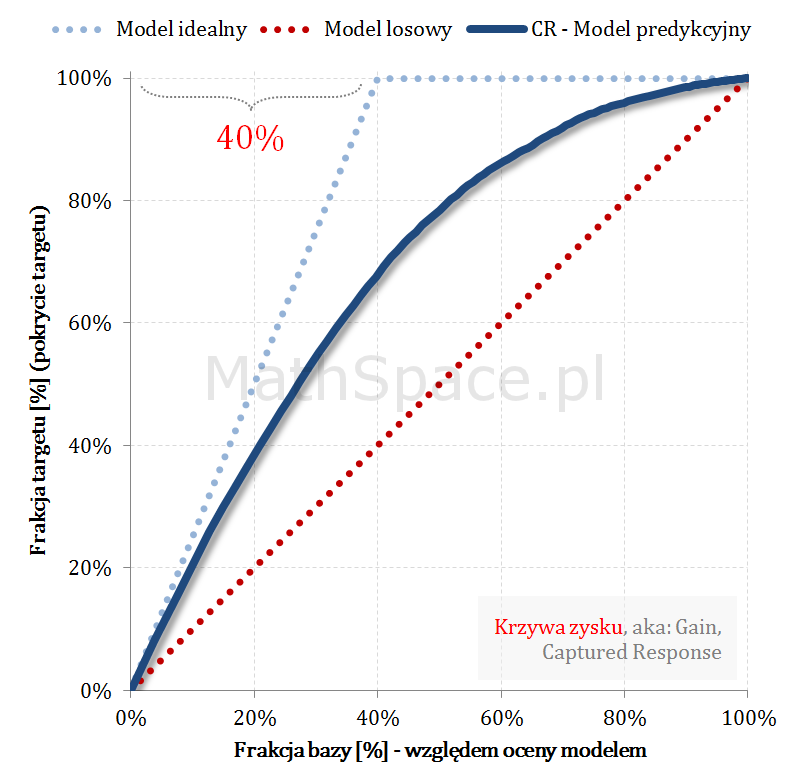
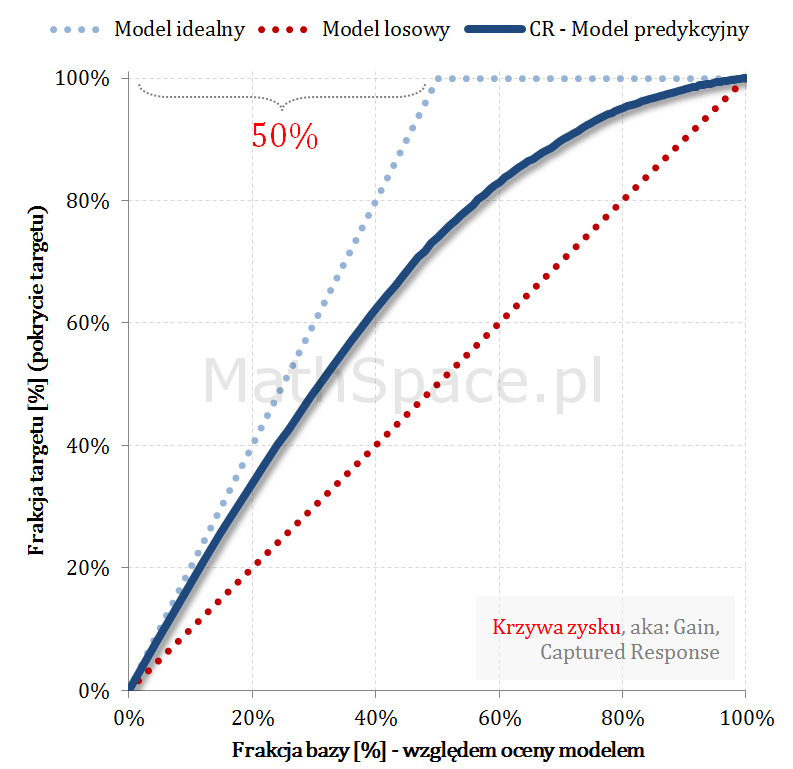
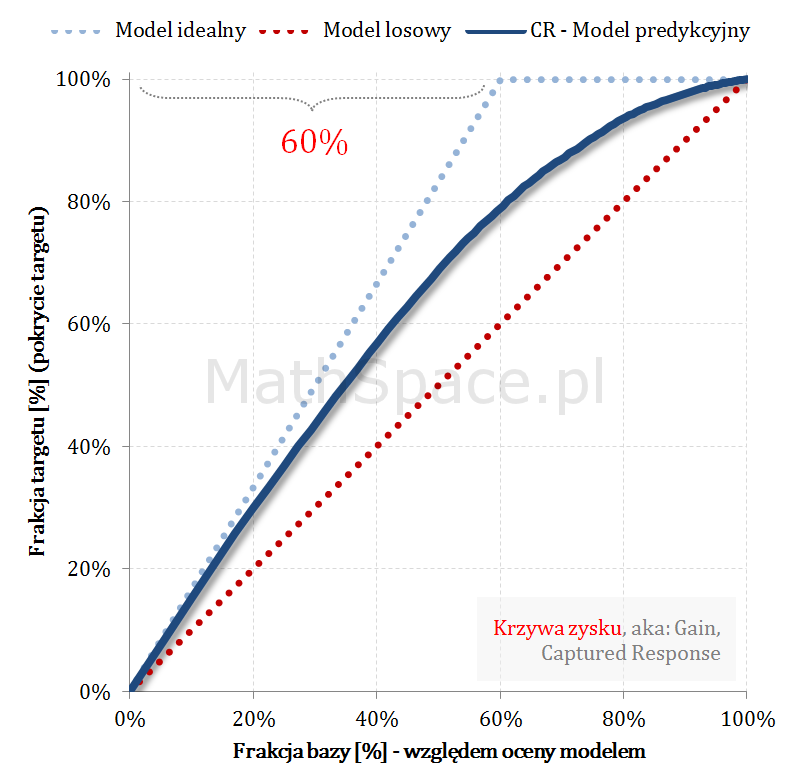
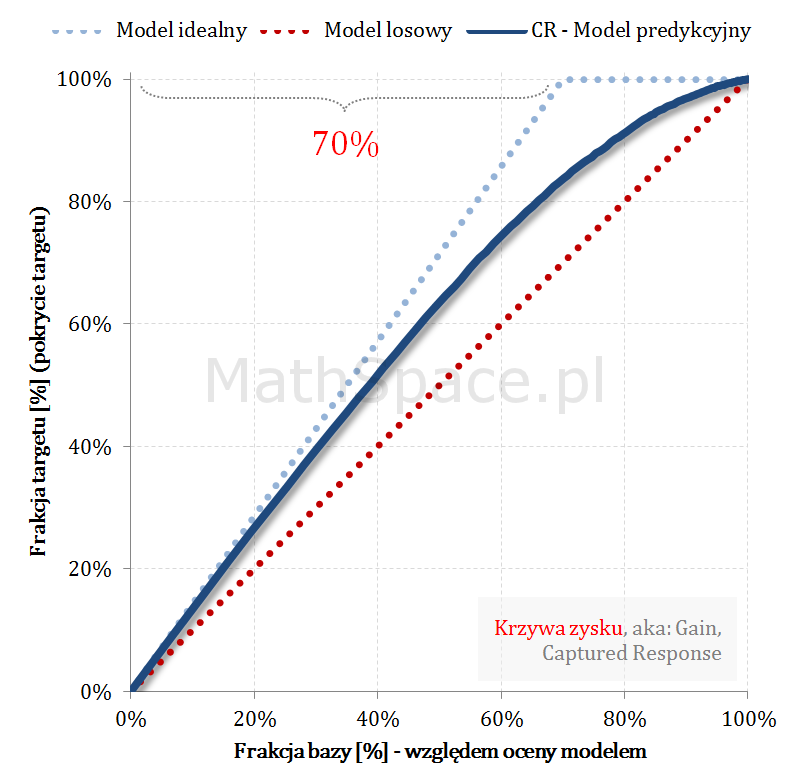
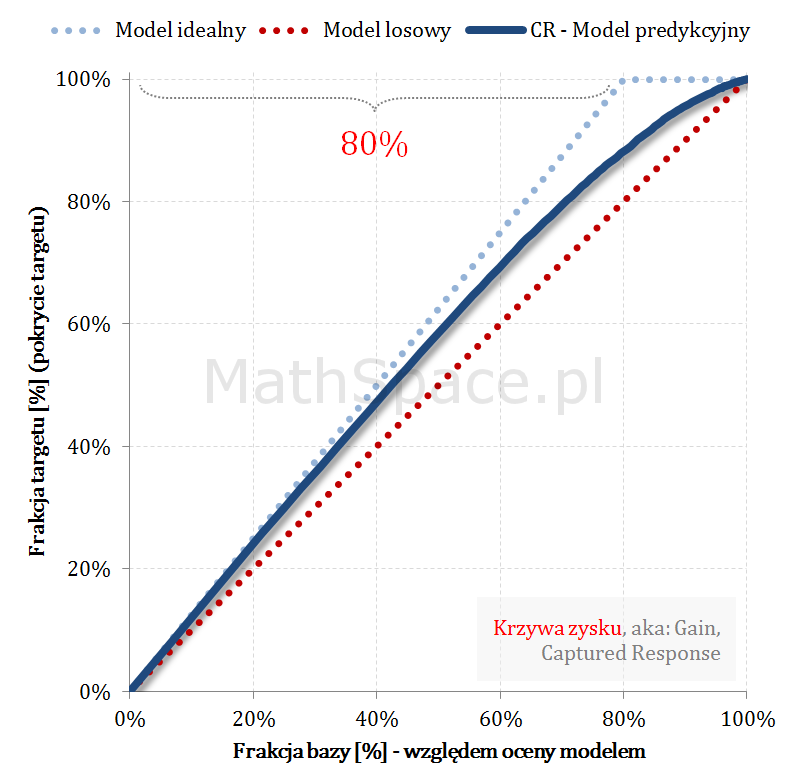
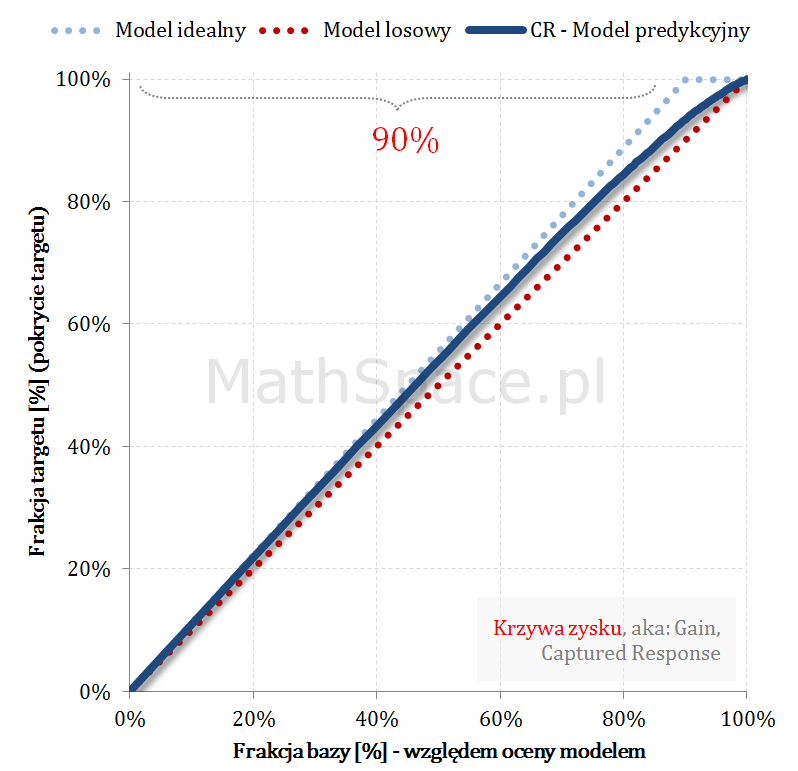
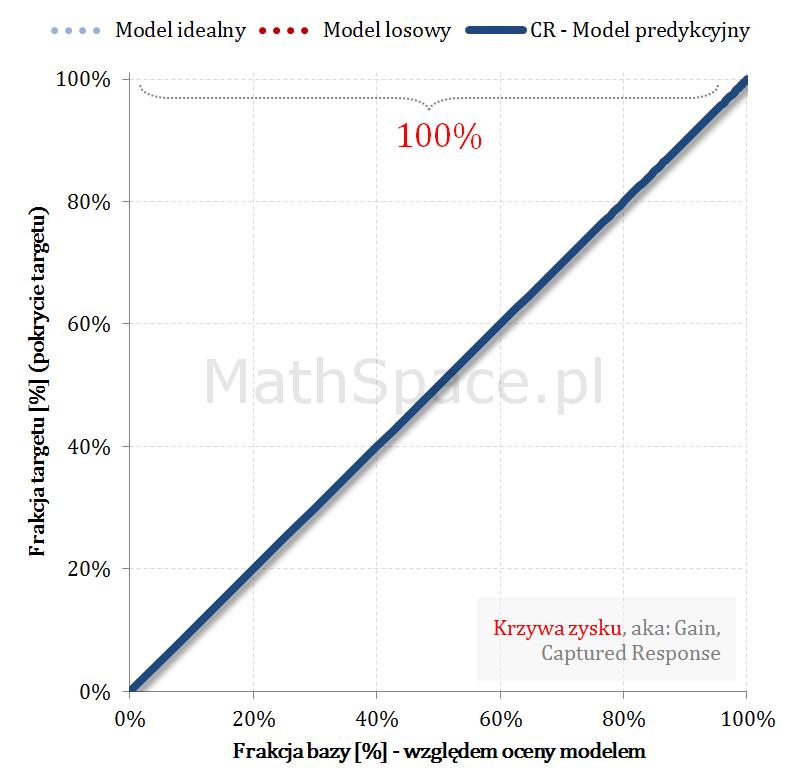
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa
Richard Feynman – Bo to jest tak, że ja muszę rozumieć świat
Richard Phillips Feynman (1915-1988) – amerykański fizyk teoretyk, niezwykle charyzmatyczna postać, nauczyciel, filozof, aktor, showman, laureat nagrody nobla z fizyki (1965 r. – tzw. diagramy Feynmana), osoba wyprzedzająca swoją epokę o całe dekady, również w kwestii nauk informacyjnych. Feynman przewidując, że klasyczne komputery nie będą w stanie rozwiązać wielu problemów, opracował podstawy komputerów kwantowych. Mistrz uwzględnienia innej perspektywy / innego punktu widzenia. Poniżej kilka cytatów autorstwa Feynmana wraz z wybranymi wywiadami / wykładami. Szczególnie polecam serię „Fun to imagine” zarejestrowaną przez BBC w roku 1983 – a najbardziej część „Why?” 🙂

„Widzisz tego ptaka? – mówił. – To gajówka Spencera (wiedziałem, że nie zna prawdziwej nazwy). – Widzisz, po włosku to jest Chutto Lapittida. Po portugalsku – Bom da Peida. Po chińsku – Chung-long-tah, a po japońsku – Katano Tekeda. Możesz poznać nazwy tego ptaka we wszystkich językach świata, ale kiedy już się ich nauczysz, nie będziesz miał o nim bladego pojęcia. Będziesz tylko wiedział, że ludzie w różnych miejscach świata tak go nazywają. Więc popatrzmy sobie na ptaszka i zobaczmy, co robi, bo to się właśnie liczy. (Bardzo wcześnie nauczyłem się, jaka jest różnica między poznaniem nazwy jakiegoś przedmiotu a wiedzą o nim).”
Richard Feynman
„Bo to jest tak, że ja muszę rozumieć świat.”
Richard Feynman
„Jest coś niedobrego z ludźmi: nie uczą się przez zrozumienie, tylko jakoś inaczej, pewnie na pamięć. Ich wiedza jest taka krucha!”
Richard Feynman
„Temu, kto nie zna matematyki, trudno spostrzec głębokie piękno przyrody.”
Richard Feynman
„Nauka to wiara w ignorancję ekspertów.”
Richard Feynman
„Przecież myślenie to tak, jakby się mówiło do siebie, w środku.”
Richard Feynman
„Nie wydaje mi się, by ten fantastycznie cudowny wszechświat, ta ogromna przestrzeń istniejąca przez tyle czasu oraz różne gatunki zwierząt, wszystkie te rozmaite planety i atomy z wszystkimi ich ruchami, i tak dalej, aby ten cały skomplikowany świat był jedynie sceną stworzoną po to, by Bóg mógł obserwować ludzi walczących o dobro i zło – a taki jest właśnie pogląd religijny. Ta scena jest zbyt duża jak na ten dramat. „
Richard Feynman
„Wydaje mi się, że znacznie ciekawiej jest żyć nie wiedząc, niż znać odpowiedzi, które mogą być błędne.”
Richard Feynman
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.