by ·0 Comments

Benoit Mandelbrot

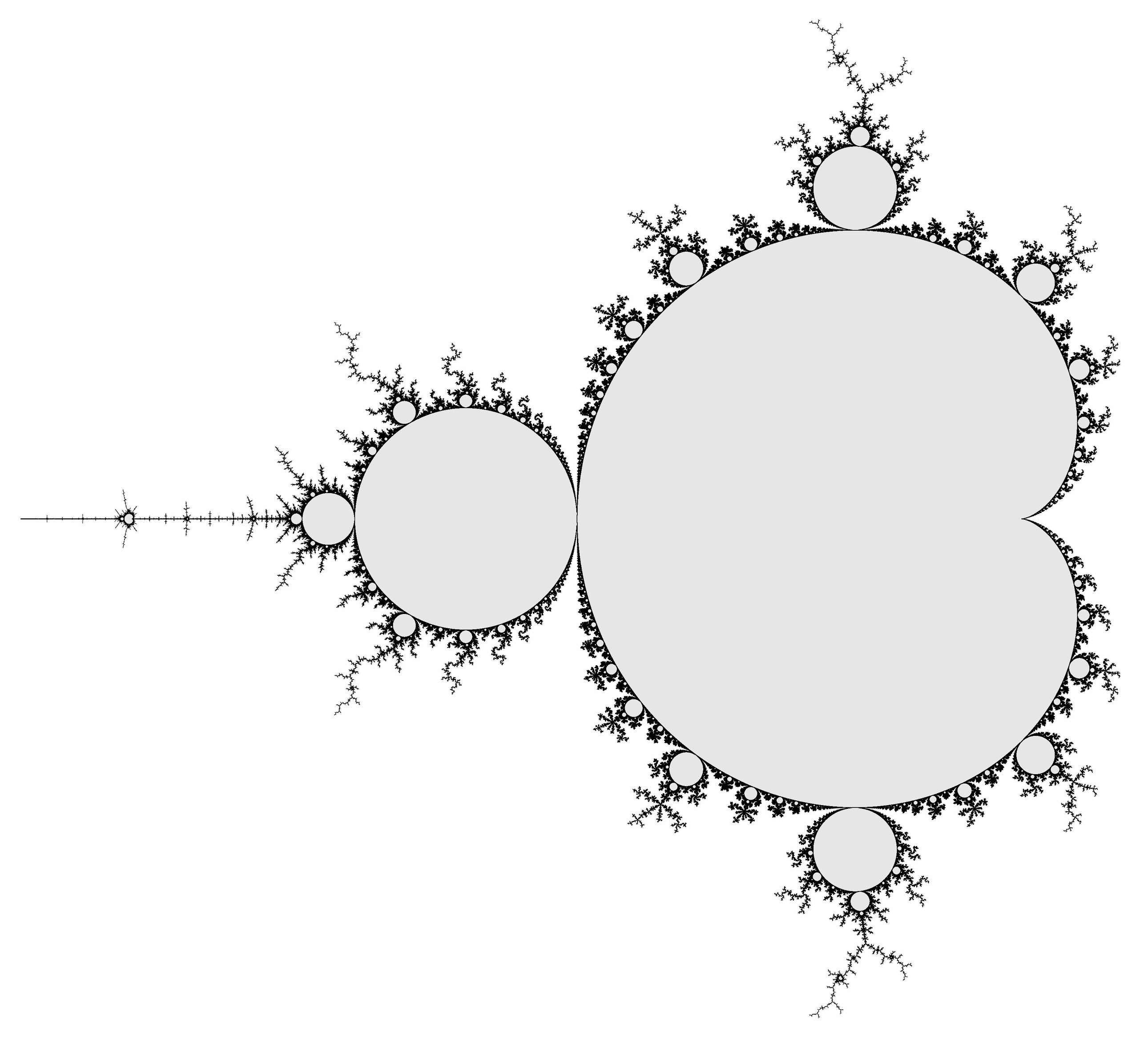
Benoit Mandelbrot

Benoit Mandelbrot (1924-2010) – twórca geometrii fraktalnej, „właściciel” prawdopodobnie najsławniejszego zbioru w matematyce – urodził się w Polsce! Przyszedł na świat w roku 1924 w Warszawie. Był dzieckiem rodziny żydowskiej, która w roku 1936 wyemigrowała do Francji, co prawdopodobnie ocaliło ich życie. Mandelbrot we Francji dołączył do swojego stryja – Szolema Mandelbrojta, również polskiego matematyka, ucznia Jacques’a Hadamarda i członka grupy Burbakiego – to Szolem wprowadził Benoit’a w świat matematyki. Mandelbrot miał niesamowitą zdolność rozwiązywania problemów poprzez wizualizację, co w tamtych czasach było niespotykane (np. grupa Burbakiego propagowała podejście niemal wyłącznie analityczne).

Historia Mandelbrota będzie z pewnością tematem osobnego wpisu, gdzie bliżej przedstawię wyniki jego prac, szczególnie te nad systemami funkcji iterowanych oraz pojęciem wymiaru fraktalnego.

Zbiór Mandelbrota

Benoit Mandelbrot – wywiad dla bigthink.com.

Zapraszam do obejrzenia wywiadu, którego Mandelrbrot udzielił dla bigthink.com.

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

https://youtu.be/YSOZPiXw6CY
I Am Here – RELEARN – Mariusz Gromada (2024)
I Am Here – RELEARN – Mariusz Gromada (2024)
https://youtu.be/XTOjmucEAsw
Deep Under – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa

by ·2 komentarze

Wszyscy doskonale znają twierdzenie Pitagorasa, jednak już znaczna mniejszość jest świadoma jego bardzo ciekawego uogólnienia, wyrażonego poniższym schematem.

Uogólnione twierdzenie Pitagorasa

Samo uogólnienie nie ogranicza się do półkoli, jest prawdziwe dla całej klasy kształtów pozostających w relacji podobieństwa, gdzie skale podobieństwa są wyrażone długościami boków trójkąta prostokątnego.

Uogólnione twierdzenie Pitagorasa

Jeśli trzy figury, względem siebie podobne, posiadają pola powierzchni odpowiednio A, B i C, oraz istnieje figura do tych trzech podobna w takich skalach podobieństwa a, b i c, że a² + b² = c² to A + B = C.

Dowód: Załóżmy, że pole figury podobnej do wskazanych trzech wynosi P. Wiemy, że pole powierzchni figur podobnych zmienia się z kwadratem skali podobieństwa (poza fraktalami, gdzie z reguły ciężko wskazać te o niezerowym polu – ale o nich tu nie mówimy), zatem:

A = P·a²            B = P·b²            C = P·c²

Wtedy

A + B = P·a² + P·b² = P(a² + b²) = P·c² = C

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

I Am Here – RELEARN – Mariusz Gromada (2024)
I Am Here – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa

by ·0 Comments

Jakiś czas temu rozważałem problem losowania ze zwracaniem dokładnie $n$-elementów z $n$-elementowego zbioru (dla uściślenia w zbiorze wyjściowym znajduje się dokładnie $n$ różnych elementów). W wyniku takiej operacji, w wylosowanej próbie, mogą pojawić się duplikaty – załóżmy zatem, że otrzymaliśmy $k$ unikalnych rezultatów (oczywiście $1\leq k\leq n$). Naturalnie pojawia się pytanie kombinatoryczne.

Losowanie ze zwracaniem

Ile istnieje sposobów takiego wylosowania (ze zwracaniem) $n$ elementów spośród $n$-elementowego zbioru, że w wyniku otrzymamy dokładnie $k$ unikalnych rezultatów?

Liczba sposobów otrzymania k-unikalnych rezultatów

Liczbę takich sposobów oznaczmy przez $B_n^k$.

„Kombinowanie” czas start! Początkowo wyszedłem od losowania $k$ różnych elementów, w kolejnym kroku planując losowanie $n-k$ z wylosowanych wcześniej $k$. Tego typu podejście prowadziło do bardzo skomplikowanych rozważań, szczegóły pominę. Na rozwiązanie wpadłem po około 2 dniach.

Wariacja bez powtórzeń

Pierwszy krok – liczba sposobów wyboru $k$ różnych elementów z $n$ zwracając uwagę na kolejność – jest to wariacja bez powtórzeń $V_n^k$.

$$V_n^k=\frac{n!}{(n-k)!}$$

Liczba Stirlinga II rodzaju

Drugi krok – zapominamy, że właśnie wylosowaliśmy $k$ unikalnych i należy jeszcze dolosować $n-k$ (choć to prawda). W zamian ustalamy, że mamy już $n$, w tym $k$ unikalnych. Trick polega na zauważeniu, że mając $k$ różnych elementów w zbiorze $n$-elementowym, dokonaliśmy jego podziału na $k$-podzbiorów.

Podział zbioru

Ile mamy sposobów podziału $n$-elementowego zbioru na $k$ podzbiorów? Jest to właśnie liczba Stirlinga II rodzaju oznaczona $S_2(n,k)$. Zatem finalnie

$$B_n^k = V_n^k\cdot S_2(n,k)$$

$$S_2(n,k)=\begin{cases}kS_2(n-1,k)+S_2(n-1,k-1)\quad\text{dla}~k<n\\S_2(n,1)=1\\S_2(n,n)=1\\S_2(n,0)=0\\S_2(0,0)=1\\S_2(n,k)=0\quad\text{dla}~k>n\end{cases}$$

Dlaczego w kroku pierwszym zwracałem uwagę na kolejność? Chętnych zapraszam do komentowania 🙂

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

I Am Here – RELEARN – Mariusz Gromada (2024)
I Am Here – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa

by ·1 Comment

MathSpace.pl – zapraszam do like’owania 🙂

 

 

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

I Am Here – RELEARN – Mariusz Gromada (2024)
I Am Here – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa

by ·0 Comments

Wielkość nieskończenie mała - Pole koła

Wielkość nieskończenie – geneza powstania

W 17 wieku Newton i Leibniz skonstruowali podstawy rachunku różniczkowego i całkowego. Ich logika opierała się na wykorzystaniu wielkości nieskończenie małej w celu wyznaczenia powierzchni pod krzywą daną równaniem funkcji. Podejście to zakładało istnienie niezerowego elementu nieskończenie małego. Filozof Leibniz poszedł dalej, gdyż ponadto uważał, że cały świat jest zbudowany z tzw. monad, czyli z substancji, które nie mają żadnej postaci, ponieważ są niepodzielne, nie mogą być ani wytworzone ani unicestwione.

Jeszcze przed naszą erą Grecy z sukcesem stosowali metodę wyczerpywania do wyznaczenia pól powierzchni figur geometrycznych. Metoda ta wykorzystywała granice, nie wykorzystywała natomiast wielkości nieskończenie małej. Jednak z metody wyczerpywania wyrosła zasada Cavalieriego, odkryta przez Archimedesa, służąca do wyznaczania objętości brył, która opierała się na argumentacji wielkości niepodzielnej.

Wielkość nieskończenie mała a skala Plancka

Intuicja podpowiada, że wielkość nieskończenie mała powinna być ekstremalnie mała, ale o niezerowym rozmiarze. W świecie praktycznym byłaby to np. wielkość mniejsza od najmniejszej teoretycznie możliwej wielkości do zmierzenia. Np. skala Plancka w fizyce dostarcza teoretycznej granicy pomiaru – nie ma możliwości skonstruowania przyrządu pomiarowego z błędem mniejszym niż skala Plancka, co nie oznacza, że poniżej skali Plancka nic nie istnieje.

Wielkość nieskończenie mała – cykl filmów od Numberphile

Numberphile logo Zapraszam do ciekawego cyklu filmów przygotowanych przez Numberphile na temat wielkości nieskończenie małych.

I na koniec jeszcze ciekawostka od MinutePhysics – Proof Without Words: The Circle.

Pozdrowienia,

Mariusz Gromada

by ·2 komentarze

Macierz pomyłek

Macierz pomyłek i klasyfikacja binarna

Macierz błędu jest podstawowym narzędziem stosowanym do oceny jakości klasyfikacji. Poniżej rozważymy przypadek klasyfikacji binarnej (dwie klasy).
Kodowanie klas:

  • 1 – Positive (np.: fakt skorzystania z produktu przez Klienta, pacjent z potwierdzoną chorobą, pacjentka z potwierdzoną ciążą)
  • 0 – Negative (np.: fakt nieskorzystania z produktu przez Klienta, pacjent z wykluczoną chorobą, pacjentka z wykluczoną ciążą)

Możliwe wyniki klasyfikacji

Macierz błędu powstaje z przecięcia klasy prognozowanej i klasy faktycznie zaobserwowanej, mamy zatem 4 przypadki (2 dla zgodności i 2 dla niezgodności prognozy ze stanem faktycznym).

  • True-Positive (TP – prawdziwie pozytywna): przewidywanie pozytywne, faktycznie zaobserwowana klasa pozytywna (np. pozytywny wynik testu ciążowego i ciąża potwierdzona)
  • True-Negative (TN – prawdziwie negatywna): przewidywanie negatywne, faktycznie zaobserwowana klasa negatywna (np. negatywny wynik testu ciążowego i brak ciąży)
  • False-Positive (FP – fałszywie pozytywna): przewidywanie pozytywne, faktycznie zaobserwowana klasa negatywna (np. pozytywny wynik testu ciążowego, jednak faktyczny brak ciąży)
  • False-Negative (FN – fałszywie negatywna): przewidywanie negatywne, faktycznie zaobserwowana klasa pozytywna (np. negatywny wynik testu ciążowego, jednak ciąża potwierdzona)
Confusion Matrix
    Stan faktyczny
    P N
Przewidywanie P TP
True-Positive		 FP
False-Positive
N FN
False-Negative		 TN
True-Negative

Przykład – do grupy 2000 osób skierowano komunikację marketingową zachęcającą do skorzystania z produktu. Spośród 2000 osób produkt zakupiło 600. Grupę 2000 podzielono losowo na dwie równoliczne części, każda po 1000 osób (w tym w każdej po 300 klientów, którzy skorzystali z produktu). Pierwszej grupie przydzielono rolę „danych uczących”, zaś drugiej rolę „danych testowych”.  Wykorzystując dane uczące, dostępne charakterystyki klientów oraz informacje o fakcie zakupienia produktu (tzw. target), przygotowano (wytrenowano / nauczono) klasyfikator umożliwiający przewidywanie czy dany klient skorzysta z produktu. Oceny jakości klasyfikatora dokonano przy wykorzystaniu danych testowych (tzn. danych, które nie były używane w procesie uczenia). Wyniki oceny zaprezentowano w postaci poniższej macierzy błędów.

Confusion Matrix dla powyższego przykładu
    Stan faktyczny
    P N
Przewidywanie P 250
True-Positive		 100
False-Positive
N 50
False-Negative		 600
True-Negative

Wnioski:

  • TP + FN + TN + FP = 250 + 50 + 600 + 100 = 1000 – liczba klientów (baza, na której dokonano oceny)
  • P = TP + FN = 250 + 50 = 300 – liczba klientów, którzy kupili produkt
  • N = TN + FP = 600 + 100 = 700 – liczba klientów, którzy nie skorzystali z produktu
  • TP + TN = 250 + 600 = 850 – liczba poprawnych klasyfikacji
  • FP + FN = 100 + 50 = 150 – liczba błędnych klasyfikacji
  • ACC = (TP + TN) / (P + N) = 850 / 1000 = 85% – jakość klasyfikacji
  • ERR = (FP + FN) / (P + N) = 150 / 1000 = 15% – poziom błędu

W kolejnych częściach przyjrzymy się innym miarom jakości klasyfikacji, które powstają z macierzy błędów.

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

I Am Here – RELEARN – Mariusz Gromada (2024)
I Am Here – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa

by ·2 komentarze

Rodzina klasyfikatorów

Temat pracy dotyczy problemu dyskryminacji oraz budowy i zastosowań rodzin klasyfikatorów, w tym głównie metody typu bagging, metody typu boosting oraz lasów losowych. Przedmiotem pracy jest zbadanie metematyczno-statystycznych fundamentów, na których opierają się metodologie budowy rodzin klasyfikatorów. Istotną częścią pracy jest analiza rozwiązań podanych zagadnień.

W pierwszym rozdziale omówiony został problem klasyfikacji pod nadzorem, zwanej analizą dyskryminacyjną. Podano model analizy dyskryminacyjnej oraz przedstawiono podstawowe metody rozwiązań podanych zagadnień. Dużo uwagi poświęcono ocenie jakości klasyfikacji.

Rozdział drugi skupia się na idei łączenia klasyfikatorów, w tym przede wszystkim na podaniu i uzasadnieniu ich zalet. Wprowadzono precyzyjną definicję rodziny oraz miarę pewności predykcji opartej na rodzinie klasyfikatorów.

Kolejne trzy rozdziały poświęcone są wspomnianym metodom łączenia klasyfikatorów w analizie dyskryminacyjnej. Rozdział trzeci omawia metodę typu bagging. Rozdział czwarty przedstawia metodę typu boosting. Natomiast rozdział piąty skupia się na metodzie lasów losowych.

Pracę kończy szeroka analiza danych, potwierdzająca własności rozważanych metod.

Autorem pracy jest Iwona Głowacka-Gromada – praca została przygotowana pod opieką Pana Profesora Jacka Koronackiego. Serdecznie zapraszam do lektury 🙂

Metody łączenia klasyfikatorów w analizie dyskryminacyjnej.

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

I Am Here – RELEARN – Mariusz Gromada (2024)
I Am Here – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa

by ·0 Comments

Analiza dyskryminacyjna

Temat pracy dotyczy problemu dyskryminacji oraz budowy drzew klasyfikacyjnych w kontekście ich przydatności do rozwiązywania zadań o dużym wymiarze prób losowych i/lub dużym wymiarze wektora obserwacji, w których podstawowego znaczenia nabiera złożoność obliczeniowa drzewa. Radzenie sobie z dużymi zbiorami danych wymaga konstrukcji specjalnych technik sortowania danych w trakcie budowy drzewa, kodowania, organizacji wzrostu i przycinania drzewa. Wymaga także zrównoleglenia obliczeń. Przedmiotem pracy jest sformułowanie modelu analizy dyskryminacyjnej oraz analiza możliwych rozwiązań podanych zagadnień, wraz z implementacją jednego z nich.

W pierwszym rozdziale omawiam problem dyskryminacji pod nadzorem, nazywanej analizą dyskryminacyjną, wprowadzając formalny model klasyfikacyjny osadzony w przestrzeni probabilistycznej.

Rozdział drugi poświęcony jest budowie drzew klasyfikacyjnych, gdzie ze szczególną uwagą potraktowano problem złożoności i skalowalności. Rozdział wprowadza formalną definicję drzewa klasyfikacyjnego w oparciu o podstawy teorii grafów oraz o model klasyfikacyjny przedstawiony w rozdziale pierwszym. Dodatkowo omawiam nowatorską technikę przycinania drzew wykorzystującą zasadę minimalnej długości kodu, MDL – Minimum Description Length (M. Mehta, J. Rissanen, R. Agrawal, 1995).

W rozdziale trzecim i czwartym skupiam się na przedstawieniu indukcji drzew decyzyjnych metodą Supervised Learning in Quest – SLIQ (M. Mehta, R. Agrawal, J. Rissanen, 1996) oraz Scalable Parallelizable Induction of Decision Trees – SPRINT (J.C. Shafer, R. Agrawal, M. Mehta, 1996).

Rozdział piąty prezentuje implementację klasyfikatora SLIQ wraz z implementacją przycinania drzew metodą MDL. Implementację przeprowadziłem we współpracy z Instytutem Podstaw Informatyki Polskiej Akademii Nauk w ramach rozwoju pakietu „dmLab”. Tekst rozdziału zawiera również analizę złożoności czasowej i skalowalności implementacji.

Pracę kończą dodatki A i B, w których zebrałem podstawowe pojęcia wykorzystane w tekście z topologii, teorii miary, probabilistyki oraz teorii grafów.

Praca została przygotowana pod opieką Pana Profesora Jacka Koronackiego. Serdecznie zapraszam do lektury 🙂

Drzewa klasyfikacyjne – ich budowa, problemy złożoności i skalowalności.

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

I Am Here – RELEARN – Mariusz Gromada (2024)
I Am Here – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa

by ·0 Comments

Nieskończoność

———————-

„Skończoność jest pożywieniem matematyki, nieskończoność – tlenem.”

———————-
„W matematyce – chodzimy na skróty przez nieskończoność.”

———————-
„Nieskończoność jest równikiem pomiędzy skończonymi biegunami założenia i tezy.”

———————-
„Do najistotniejszych pojęć matematyki należą mosty łączące skończoność i nieskończoność.”

———————-

Leżącą cyfra osiem, lemniskata ∞, dobrze wszystkim znany symbol nieskończoności. Czasami z plusem, czasami z minusem, innym razem samotnie, ale zawsze od początku do końca, od zera do krańca wszystkiego. Pojęcie nieskończoności pojawia się w wielu dziedzinach. Świat fizyki zastanawia się czy Wszechświat jest nieskończony? Czy istnieje nieskończoność w mikroskali? Czy materię można dzielić na coraz mniejsze części, powtarzając czynność bez końca? Świat werbalny przedstawia nieskończoność jako granicę, jako zjawisko cykliczne, jako abstrakcję. Boskość wraz z wiecznością silnie wiążą się z nieskończonością dla świata duchowego. Nawet w świecie komputerów prosty błąd programisty może doprowadzić do nieskończonej pętli. Wiele możliwości interpretacji, wiele typów nieskończoności, a świat matematyki dostarcza kolejnych. Dlatego zapraszam wszystkich do poznania wielu różnych oblicz nieskończoności w matematyce, do zrozumienia, że istnieją te mniejsze i te większe, że nie istnieje największa, że jednocześnie możemy wskazać nieskończoność najmniejszą – i bardziej ogólnie – że istnieją metody porównywania rozmiarów nieskończoności!

Zapraszam do eseju „Od paradoksów do hipotezy continuum – czyli tajemnice nieskończoności.”

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

https://youtu.be/YSOZPiXw6CY
I Am Here – RELEARN – Mariusz Gromada (2024)
I Am Here – RELEARN – Mariusz Gromada (2024)
https://youtu.be/XTOjmucEAsw
Deep Under – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa

by ·0 Comments

Wymiar fraktalny (nazywany czasami wymiarem samopodobieństwa) ma wiele definicji. Większość z nich opiera się na własności samopodobieństwa. Wymiar fraktalny niesie w sobie bardzo ciekawą informację – pokazuje w jakim stopniu obiekt wypełnia przestrzeń, w której jest osadzony. Dla regularnych obiektów (np. kula, kostka) osadzonych w przestrzeniach n-wymiarowych, wymiar fraktalny wyniesie n (np. wymiar fraktalny kuli 2-wymiarowej wynosi 2), wskazując, że te obiekty w „100% wypełniają” przestrzeń, w której są osadzone. W przypadku fraktali ich wymiar fraktalny jest mniejszy od wymiaru przestrzeni, w której się znajdują – i co bardziej istotne – będzie niecałkowity (a nawet niewymierny). To fascynujące, że takie obiekty istnieją, a geometria fraktalna jest językiem biologii! Wszystkich chętnych do zapoznania się z intuicyjną definicję wymiaru fraktalnego (dla szczególnych klas obiektów i przestrzeni – takich jak przestrzenie metryczne), zapraszam do mojego mini artykułu Fraktale – jako obrazy matematycznego świata zbiorów (fraktale i samopodobieństwo).

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

I Am Here – RELEARN – Mariusz Gromada (2024)
I Am Here – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa