Georg Ferdinand Ludwig Philipp Cantor (1845 – 1918) – niemiecki matematyk, który zainicjował (oraz znacząco rozwinął) teorię mnogości. Można powiedzieć, że „Cantor dla teorii mnogości jest tym, kim Mandelbrot dla geometrii fraktalnej”. Cantora osobiście zaliczam do grona gigantów matematyki, których koncepcje i wyniki prac znacząco wyprzedzały daną epokę. Cantor jako pierwszy zadał pytanie o rozmiar nieskończoności. Wprawdzie w 17 wieku Newton i Leibniz stosowali pojęcie wielkości nieskończenie małej o niezerowym rozmiarze, co zapoczątkowało rachunek różniczkowy i całkowy – w 2015 roku napisałem na ten temat kilka słów. Ich starania nie były precyzyjne i w zasadzie jedynie „mgliście” wykorzystywały przejście w krok nieskończony, pomijając szereg problemów z tym związanych.
Cantor zajął się prawdziwie aktualną nieskończonością, wprowadzając definicję równoliczności zbiorów (również tych nieskończonych), co pozwoliło uogólnić pojęcie liczności zbioru. Dziś moc zbioru, określana mianem liczby kardynalnej i oznaczana $|A|$, odnosi się do wskazania zbioru równolicznego (na bazie istnienia bijekcji – czyli jednoznacznego parowania elementów dwóch zbiorów – co działa również w przypadku nieskończonym), którego moc jest znana. Idąc dalej – Cantor w liczbach kardynalnych wprowadził porządek. Powiemy, że $|A|\leq |B|$ jeśli A jest równoliczne z podzbiorem B.
Na mocy twierdzenie Cantora-Bernsteina otrzymujemy, że
jeśli $|A|\leq |B|$ oraz $|B|\leq |A|$ to $|A|=|B|$
Wynik genialny, gdyż pozwala porządkować również zbiory nieskończone! Cantor uczynił ten krok, wskazał nieskończoność najmniejszą – tj. nieskończoność zbioru liczb naturalnych. Zbiory równoliczne ze zbiorem liczb naturalnych nazywamy dziś nieskończonymi zbiorami przeliczalnymi o mocy $\aleph_0$ (czyt. aleph zero).
W 1890 roku Cantor udowodnił przełomowe twierdzenie mówiące, że każdy zbiór ma mniejszą moc niż zbiór jego podzbiorów (zbiór potęgowy).
$$|A|< |2^A|$$
Kolejny genialny wynik, dający „generator” coraz to „większych” nieskończoności. Tych większych nieskończoności nie trzeba było szukać bardzo daleko. Analizując zbiór liczb rzeczywistych Cantor stwierdził, że jego nieskończoność znacznie przewyższa nieskończoność liczb naturalnych. Nieskończoność zbioru liczb rzeczywistych nazywamy dziś continuum i oznaczamy $\mathfrak{c}$.
$$\mathfrak{c}=2^{\aleph_0}$$
Czy istnieje nieskończoność większa od nieskończoności liczb naturalnych oraz mniejsza od nieskończoności liczb rzeczywistych? To pytanie również postawił Cantor, niestety na swoje nieszczęście… Pytanie, nazywane dziś Hipotezą Continuum, doprowadziło Cantora do choroby psychicznej. Cantor do końca życia przekonany był – na zmianę – o prawdziwości / nieprawdziwości hipotezy, co rusz przesyłając dowody potwierdzające / zaprzeczające. Dopiero w 1963 roku Paul Cohen wykazał, że Hipoteza Coninuum jest niezależna od aksjomatów teorii mnogości – czyli, że na bazie tych aksjomatów, nie można jej ani wykazać ani zaprzeczyć…
Zdecydowałem się na ten nieco długi, nie do końca związany z geometrią fraktalną, wstęp, ze względu na wpływ, jaki wywarły na moją osobę idee Georga Cantora. W 2007 roku napisałem artykuł „Od paradoksów do Hipotezy Continuum czyli – Tajemnice Nieskończoności” – zapraszam do lektury wszystkich pragnących zgłębić pojęcie nieskończoności w matematyce.
Polecam również „A Hierarchy of Infinities” – odcinek z serii „PBS Infinite Series”.
Zbiór Cantora
Zbiór Cantora jest podzbiorem jednostkowego odcinka powstającym poprzez:
- podział odcinka na 3 równe części;
- usunięcie części środkowej;
- powtórzenie procedury usuwania dla nowo powstałych odcinków.
Finalny zbiór Cantora jest zbiorem granicznym przy nieskończenie wielu iteracjach wykonanych zgodnie z powyższymi punktami.
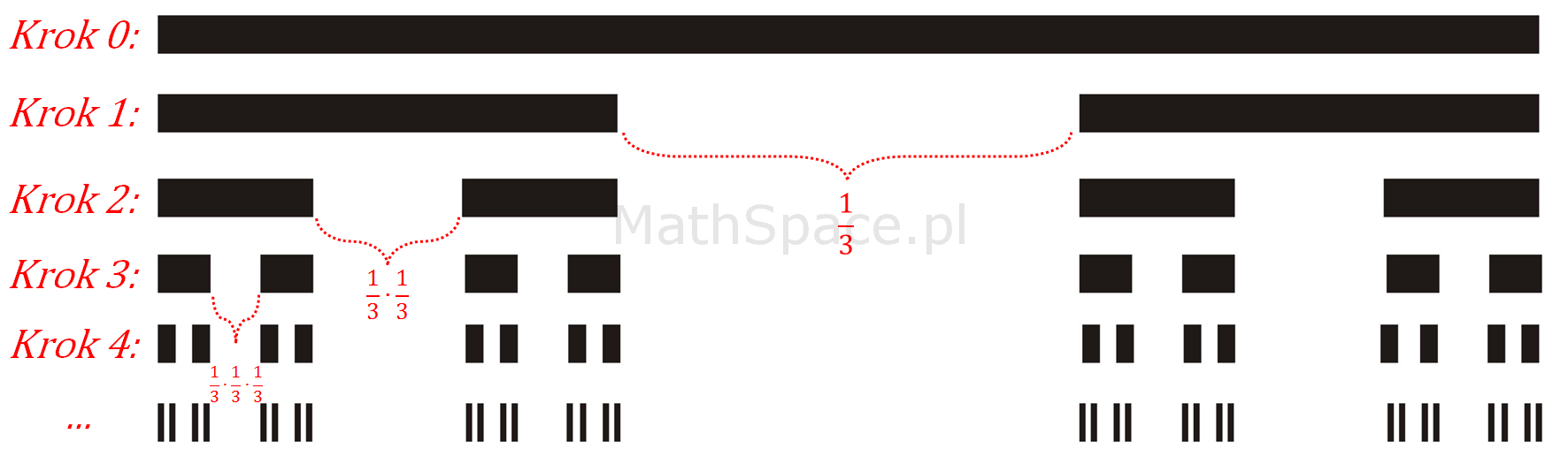
Zbiór Cantora został przez opisany w roku 1883.
Niezwykłe właściwości zbioru Cantora
- Długość zbioru Cantora jest równa 0 – w języku bardziej formalnym powiemy, że jest to zbiór miary 0 (w sensie miary Lebesgue’a).
Zbiór Cantora powstaje poprzez usuwanie pewnych części – policzmy długość odcinków usuniętych.
$$1\cdot\frac{1}{3}+2\cdot\frac{1}{9}+4\cdot\frac{1}{27}+\ldots+2^{n-1}\cdot\frac{1}{3^n}+\ldots=$$
$$=\displaystyle\sum_{n=1}^{\infty}\frac{2^{n-1}}{3^n}=\displaystyle\sum_{n=1}^{\infty}\frac{2^{n-1}}{3\cdot 3^{n-1}}=$$
$$=\displaystyle\sum_{n=1}^{\infty}\frac{1}{3}\bigg(\frac{2}{3}\bigg)^{n-1}=\frac{1}{3}\cdot\frac{1}{1-\frac{2}{3}}=1$$
Długość odcinków usuniętych jest równa jedności, zatem to co pozostało musi mieć długość równą 0 🙂
- Zbiór Cantora jest równoliczny ze zbiorem liczb rzeczywistych $\mathbb{R}$ – czyli ma moc continuum $\mathfrak{c}$.
Jest to dość zaskakująca własność dla zbioru, który nie ma długości (co pokazaliśmy wyżej). Zbiór Cantora ma formę „rozdmuchanego pyłu”, mimo to punktów jest znacznie więcej niż liczb naturalnych. Szczegóły dowodu relacji równoliczności znajdziecie tutaj.
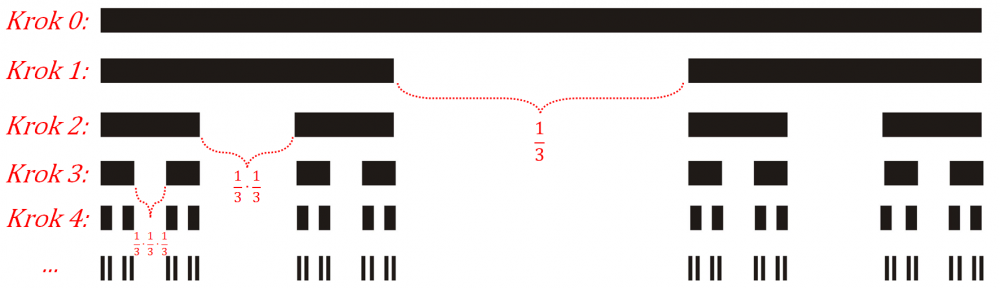
- Zbiór Cantora posiada własność samo-podobieństwa – czyli, że w jego skład wchodzą „jego mniejsze kopie”.

Własność samo-podobieństwa wynika wprost z definicji zbioru. Powyżej na obrazku zaznaczyłem część zbioru podobną do jego całości.
Zbiór Cantora jako fraktal
Zbiór Cantora posiada nietrywialną strukturę w każdej skali i jest samo-podobny – jest to zatem fraktal, najprostszy z możliwych 🙂
Iloczyn kartezjański zbiorów Cantora
Georg Cantor – ciekawostki
- Był uczniem Karla Weierstrass’a oraz Leopolda Kronecker’a.
- Przyjaźnił się z Richardem Dedekind’em – pamiętacie przedziały Dedekinda i liczby rzeczywiste? 🙂
- Był osobą bardzo wierzącą. Odkrywając tajemnice nieskończoności odnosił wrażenie, że to sam Bóg mu je przekazuje.
- Z powodu niemożności rozwiązania Hipotezy Continuum popadł w ciężką depresję, był wielokrotnie hospitalizowany, nie odzyskał w pełni zdrowia.
- W ostatnich latach życia zajmował się mistycyzmem rozwijając koncepcję Absolutnej Nieskończoności, którą utożsamiał z Bogiem.
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.




 Zapraszam do ciekawego cyklu filmów przygotowanych przez
Zapraszam do ciekawego cyklu filmów przygotowanych przez