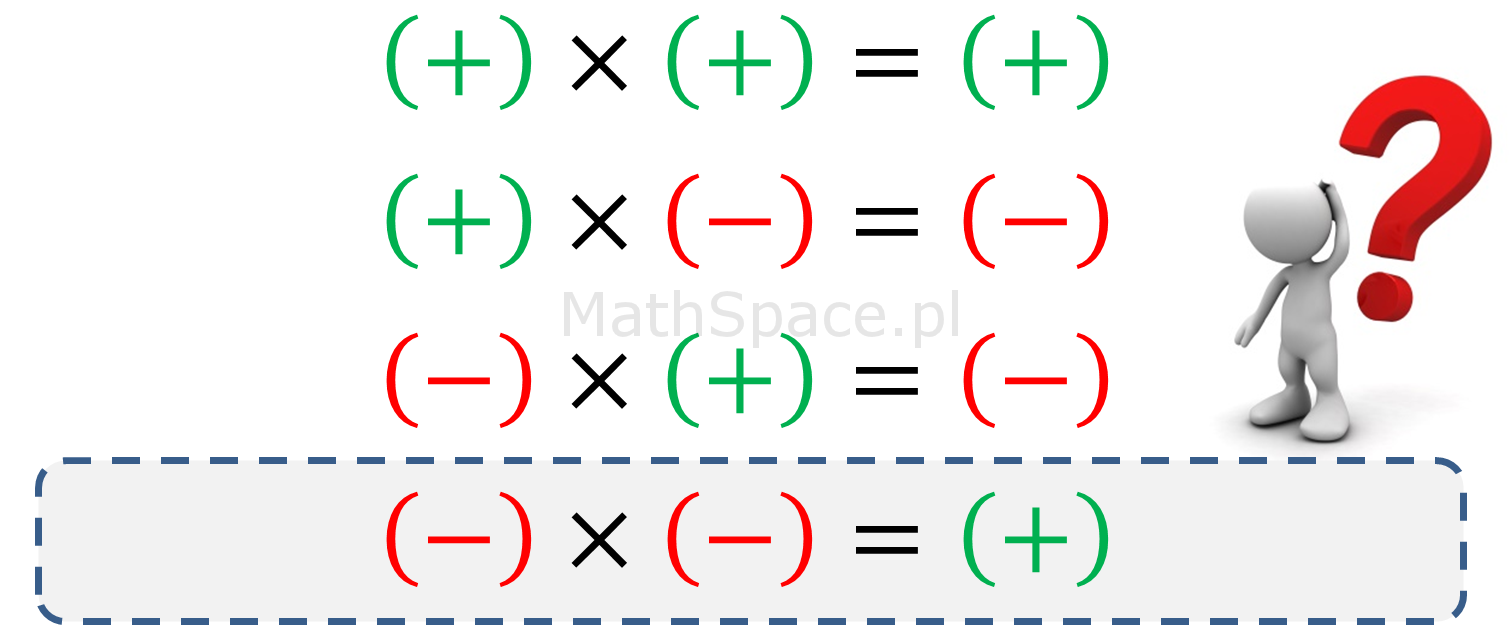
Z pewnością każdy wie, że wynikiem mnożenia liczb ujemnych jest liczba dodania. Formułka „minus razy minus daje plus” była nam wtłaczana do głów w trakcie wczesnych lat szkolnych. Nauczyciele zapomnieli jednak wyjaśnić dlaczego tak właśnie jest, oraz przybliżyć motywację matematyków definiujących arytmetykę liczb ujemnych.
Mnożenie jako skrócone dodawanie
Mówi się, że mnożenie to skrócone dodawanie, co jest w zupełności prawdą i, przy ograniczeniu do liczb całkowitych, faktem dosyć oczywistym.
$$3\times 4 = 3 + 3 + 3 + 3 = 4 + 4 + 4 = 12$$
Mnożenie jest przemienne i rozdzielne względem dodawania
Te dwie fundamentalne własności mnożenia zapisujemy jako
przemienność $a\times b = b\times a$
przykład $3\times 4 = 4\times 3=12$
rozdzielność $a\times (b+c)=a\times b + a\times c$
przykład $3\times 4 = 3\times (1+3) = 3\times 1 + 3\times 3 = 3 + 9 = 12$
Mnożenie liczb ujemnych z punktu widzenia matematyka
Matematycy, definiując arytmetykę liczb ujemnych, chcieli zachować spójność z już rozwiniętą arytmetyką liczb dodatnich i zera. Opierając się na interpretacji skróconego dodawania łatwo uzasadniamy następujące:
$$-3\times 4 = (-3)+(-3)+(-3)+(-3)=-12$$
„Dodając dług do długu” otrzymujemy większy dług – intuicyjne. Teraz wykorzystując przemienność mnożenia otrzymujemy:
$$4\times (-3)=-3\times 4=-12$$
W tym momencie z intuicją już trochę trudniej, natomiast spójność została zachowana. Czas przejść do meritum – tzn spróbujmy odpowiedzieć na pytanie:
$$-3\times (-4)=?$$
Do rozwiązania powyższego zastosujemy trick na bazie rozdzielność mnożenia względem dodawania.
$$-3\times 0=0$$
$$-3\times 0=-3\times(-4+4)=0$$
$$-3\times(-4+4)=-3\times (-4)+(-3)\times 4=0$$
$$-3\times(-4)+(-12)=0$$
$$-3\times(-4)=12$$
Powyższe z intuicją nie ma nic wspólnego, jednak jest spójne, tzn. na bazie arytmetyki liczb dodatnich i zera, przemienności mnożenia, rozdzielności mnożenia względem dodawania, jesteśmy w stanie uzasadnić dlaczego mnożenie liczb ujemnych musi być liczbą dodatnią.
Mnożenie liczb ujemnych jako zmniejszenie straty
Załóżmy, że mnożymy dwie liczby, gdzie interpretacja pierwszej to wartość zysku bądź starty, natomiast znaczenie drugiej to zwielokrotnienie (zwiększenie / zmniejszenie) pierwszej wartości. W takiej sytuacji mnożenie dwóch liczb ujemnych oznacza zmniejszenie straty, czyli łączny efekt dodatni działania.
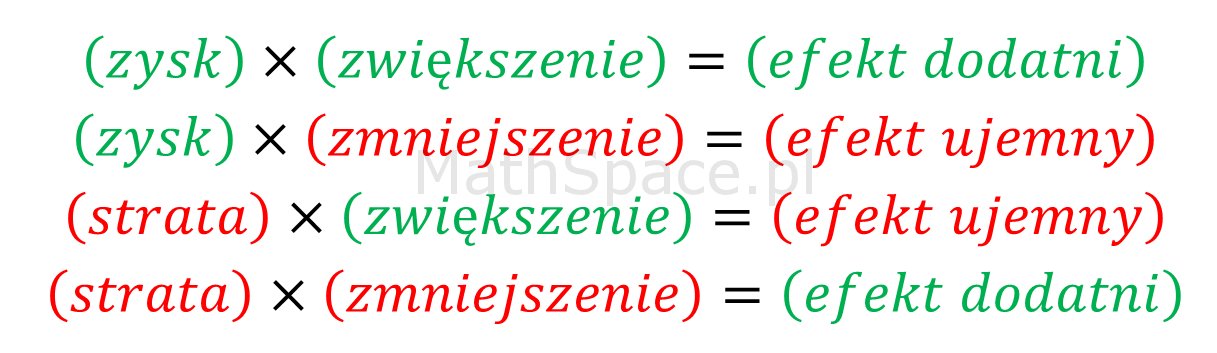
Powyższe wyjaśnienie można określić mianem intuicyjnego 🙂
I na koniec film od Mathologer’a wyjaśniający powyższy problem (materiał, na którym wzorowałem powyższy wpis).
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
