Cykl „Matematyka w obrazkach” – część #12 – Devil vs Evil – rozstrzygamy co było pierwsze 🙂
Znasz odpowiedź? Wpisz w komentarzu 🙂
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa
Views All Time
3626
Views Today
5
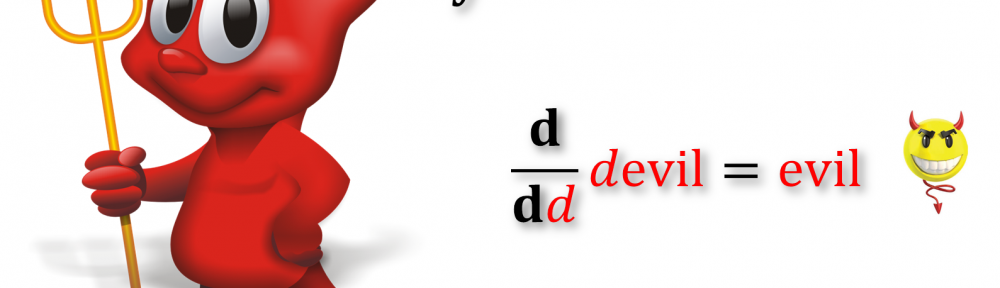
jakbyś to trochę popodnosił i poopuszczał to łatwiej byłoby te pochodne liczyć 🙂
Dobra to ja zacznę:
Całka nieznaczona z xdy wynosi xy+C (constant)
mnożenie jest przemienne więc całka nieoznaczona z evil dd daje devil+C.
Tyle o górnej łamigłówce.
Dolną najprościej byłoby poskreślać ułamkami licząc że to zmienne ale tak nie jest.
Przychodzi mi tylko na myśl tylko to że: f`(x)=df/dx Lagrange?
i że dy/dx bierze pochodną y w odniesieniu do x. A d/dx bierze pochodną w odniesieniu do x ale…nie do końca bo zakładamy że y jest naszym dowolnym wyrażeniem z którego możemy wyliczyć pochodną. Brak mi właśnie tego wyrażenia. Na dziś dam sobie spokój pomyślę jutro.
To jest jedna łamigłówka 🙂 Trzeba odpowiedzieć co było pierwsze 🙂 Devil czy Evil? 🙂
BTW: górna poprawnie odczytana, dolna przekombinowałeś 🙂 Podpowiedź: ile to jest np. d/dx x^2*a ? Albo d/dx x^3*a ?
Przekombinowałem. Jedyne co mi teraz przychodzi do głowy to to, że pochodna z x*n wynosi n, więc jeśli wynikiem miałby być devil to potrzebujemy jednego plemnika. Na 10 devili potrzeba 10 evili (evil=0 odpada). Skoro pochodna jest zmianą wartości funkcji względem zmian jej argumentów to im więcej devili tym więcej evili 🙂 A że grzech nie jest tam obcy więc tworzymy ładne piekiełko. Moim zdaniem evil był pierwszy.