Wnioskowanie indukcyjne
Rozumowaniem indykcyjnym określa się wnioskowanie „od szczegółu do ogółu”, przez co indukcja bywa uważana za jedno z głównych narzędzi tzw. nauk empirycznych (metody polegające na zastosowaniu eksperymentu, obserwacji, indukcji enumeracyjnej oraz indukcji eliminacyjnej).
Wnioskowanie dedukcyjne
Rozumowaniem dedukcyjnym określa się wnioskowanie „od ogółu do szczegółu”. Dedukcja jest podstawowym narzędziem stosowanym w logice i matematyce, gdzie z twierdzenia ogólnego (bądź założenia / aksjomatu) wysuwa się wniosek bardziej szczegółowy. Dedukcja jest także często wykorzystywana w naukach opierających się na doświadczeniach empirycznych, gdzie dobrym przykładem jest fizyka teoretyczna, która często wyprowadza twierdzenia i wnioski potwierdzane (lub nadal nie) eksperymentalnie dopiero po wielu latach (np. Ogólna Teoria Względności, Promieniowanie Hawkinga).
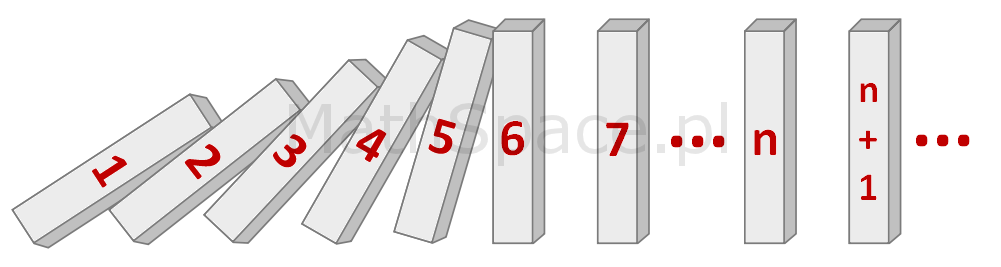
Indukcja matematyczna
Twierdzenie: Jeżeli:
- istnieje taka liczba naturalna $n_0$, że $T(n_0)$ jest zdaniem prawdziwym,
- dla każdej liczby naturalnej $n \geq n_0$ z założenia prawdziwości zdania $T(n)$ wynika prawdziwość zdania $T(n+1)$
to $T(n)$ jest zdaniem prawdziwym dla każdego naturalnego $n \geq n_0$.
Przykład: Udowodnić, że dla każdej naturalnej liczby $n \geq 3$ spełniona jest nierówność $2^n > 2n$.
Forma zdaniowa $T(n)$ przyjmuje postać $T(n) : 2^n > 2n$, gdzie $n_0 = 3$
- dla $n=3$ mamy $2^3 = 8 > 2 \cdot 3 = 6$,
- zakładamy, że nierówność $2^n > 2$$ jest prawdziwa dla $n \geq 3$ – przeprowadzany mnożenie nierówności przez $2$:
$$2 \cdot 2^n > 2 \cdot 2n$$
$2^{n+1} > 2n+2n$, ale dla $n \geq 3$ mamy $2n > 2$, zatem
$2^{n+1} > 2n+2 = 2(n+1)$, ostatecznie
$$2^{n+1} > 2(n+1)$$
Nierówność powyższa oznacza, że z założenie prawdziwości $T(n)$ wynika prawdziwość $T(n+1)$, co na podstawie twierdzenia o indukcji matematycznej kończy dowód.
Wniosek: Stosując ogólne twierdzenie (zasadę indukcji matematycznej) wykazaliśmy prawdziwość wniosku szczegółowego (tzn. poprawność wyżej opisanej nierówności) – zatem stosowanie zasady indukcji matematycznej jest wnioskowaniem dedukcyjnym 🙂 .
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
