Ze statystyk odwiedzin wynika, że cykl „Ocena jakości klasyfikacji” cieszy się Waszym zainteresowaniem – zatem wracam do tej tematyki. Dziś przedstawię wstęp do analizy jakości modeli predykcyjnych, skupiając się na jednym tylko aspekcie jakości – tzn. na sile modelu w kontekście separacji klas. Zapraszam 🙂
Jakość modelu predykcyjnego
Matematyka dostarcza wielu różnych miar służących ocenie siły modelu predykcyjnego. Różne miary są często ze sobą mocno powiązane, i choć przedstawiają bardzo podobne informacje, umożliwiają spojrzenie na zagadnienie z innych perspektyw. Przez jakość modelu predykcyjnego rozumiemy typowo ocenę jakości w trzech obszarach:
- Analiza siły separacji klas – czyli jak dalece wskazania modelu są w stanie „rozdzielić” faktycznie różne klasy pozytywny i negatywne;
- Analiza jakość estymacji prawdopodobieństwa – bardzo ważne w sytuacjach wymagających oceny wartości oczekiwanych, tzn. poszukujemy wszelkiego rodzaju obciążeń (inaczej – błędów systematycznych);
- Analiza stabilności w czasie – kluczowy aspekt rzutujący na możliwość wykorzystywania modelu w faktycznych przyszłych działaniach.
Wszystkie wymienione obszary są ze sobą powiązane terminem prawdopodobieństwa, za pomocą którego można wyrazić zarówno siłę separacji, jak też stabilność w czasie.
Założenia
Podobnie do poprzednich część cyklu załóżmy, że rozważamy przypadek klasyfikacji binarnej (dwie klasy: „Pozytywna – 1” oraz „Negatywna – 0”). Załóżmy ponadto, że dysponujemy modelem predykcyjnym $p$ zwracającym prawdopodobieństwo $p(1|x)$ przynależności obserwacji $x$ do klasy „Pozytywnej -1” (inaczej „P od 1 pod warunkiem, że x”). I jeszcze ostatnie założenie, wyłącznie dla uproszczenia wizualizacji i obliczeń – dotyczy rozmiaru klasy pozytywnej – ustalmy, że jej rozmiar to 20%, inaczej, że prawdopodobieństwo a-priori P(1)=0.2.
Model predykcyjny a siła separacji klas – nieskumulowane prawdopodobieństwo
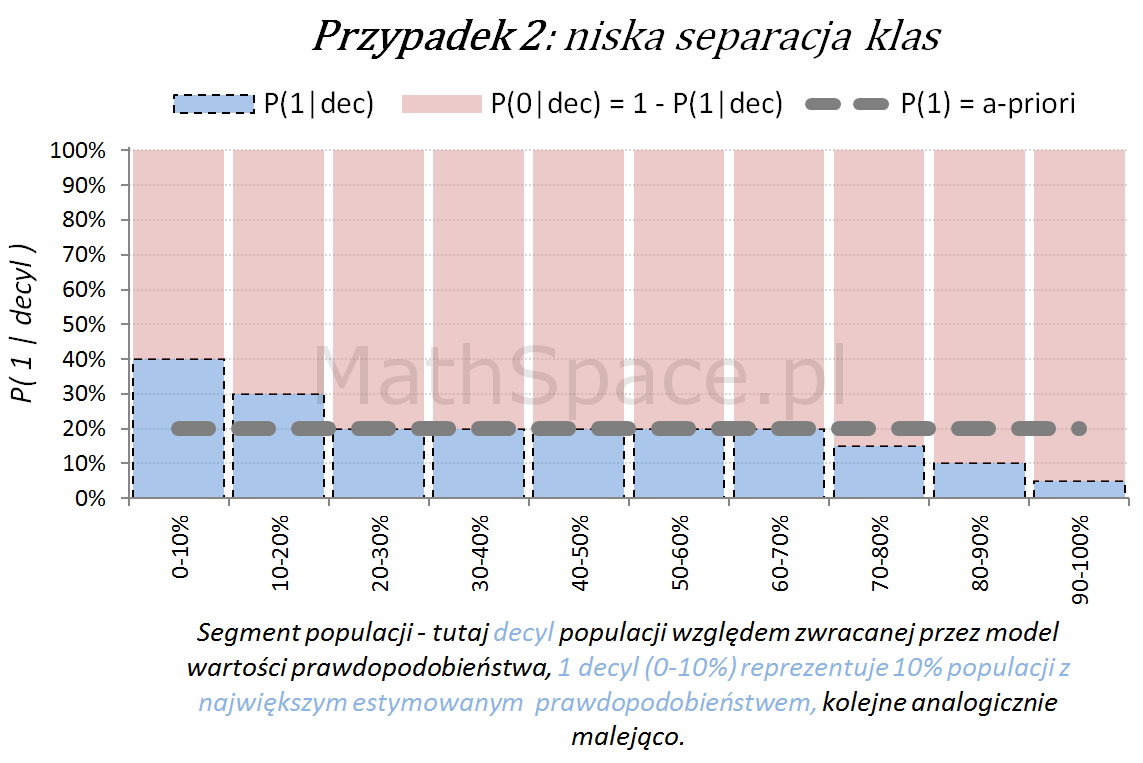
Poniżej przedstawiamy różne przypadki wizualnej oceny siły modelu. Interpretacja zamieszczonych wykresów jest następująca:
- Oś pozioma reprezentuje kolejne segmenty populacji, tu zostały użyte decyle bazy względem zwracanej wartości prawdopodobieństwa przez model. Zatem 1 decyl agreguje 10% populacji z największym estymowanym prawdopodobieństwem, kolejne decyle – analogicznie.
- Oś pionowa przedstawia prawdopodobieństwo warunkowe, że obserwacja z danego segmentu populacji (tutaj decyl bazy) faktycznie pochodzi z klasy „Pozytywnej – 1”.
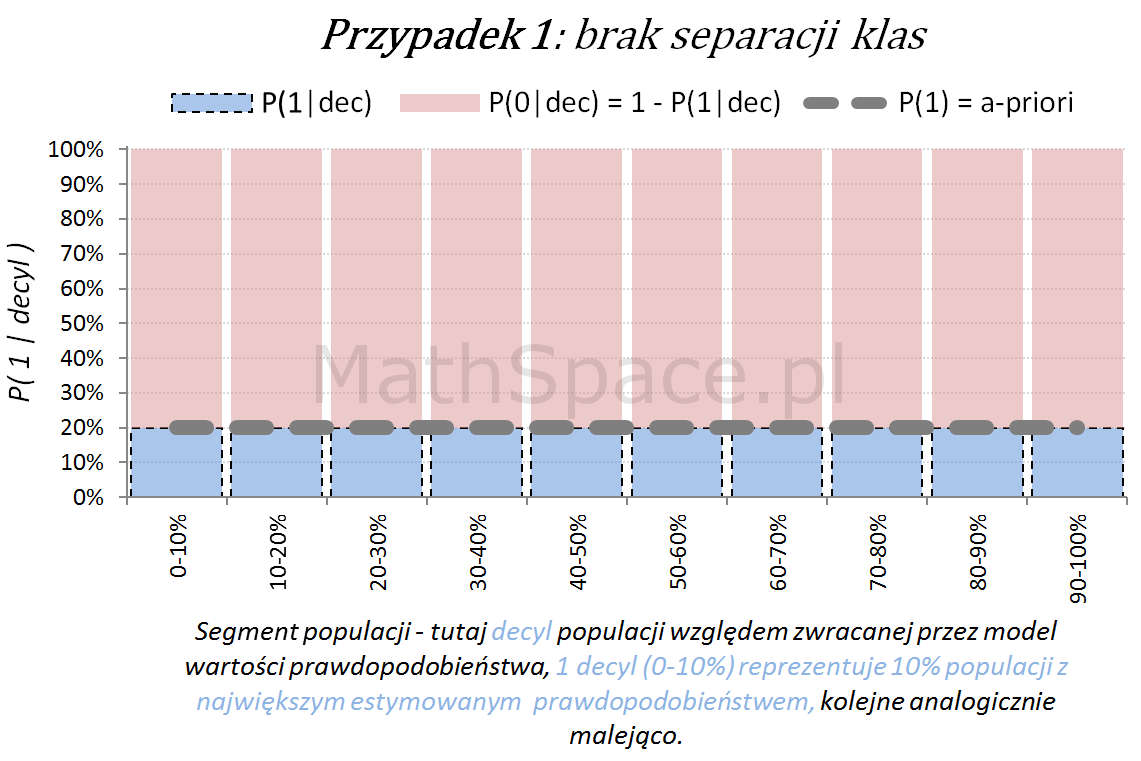
Naturalnym jest, że model predykcyjny posiadający dodatnią siłę separacji klas, wykorzystany do podziału populacji na segmenty względem wartości malejącej (tutaj 10 decyli), powinien wpłynąć na faktyczną częstość obserwacji klasy „Pozytywnej – 1”. Tzn. w pierwszych decylach powinniśmy widzieć więcej klasy „1” – kolejne przykłady właśnie to obrazują.
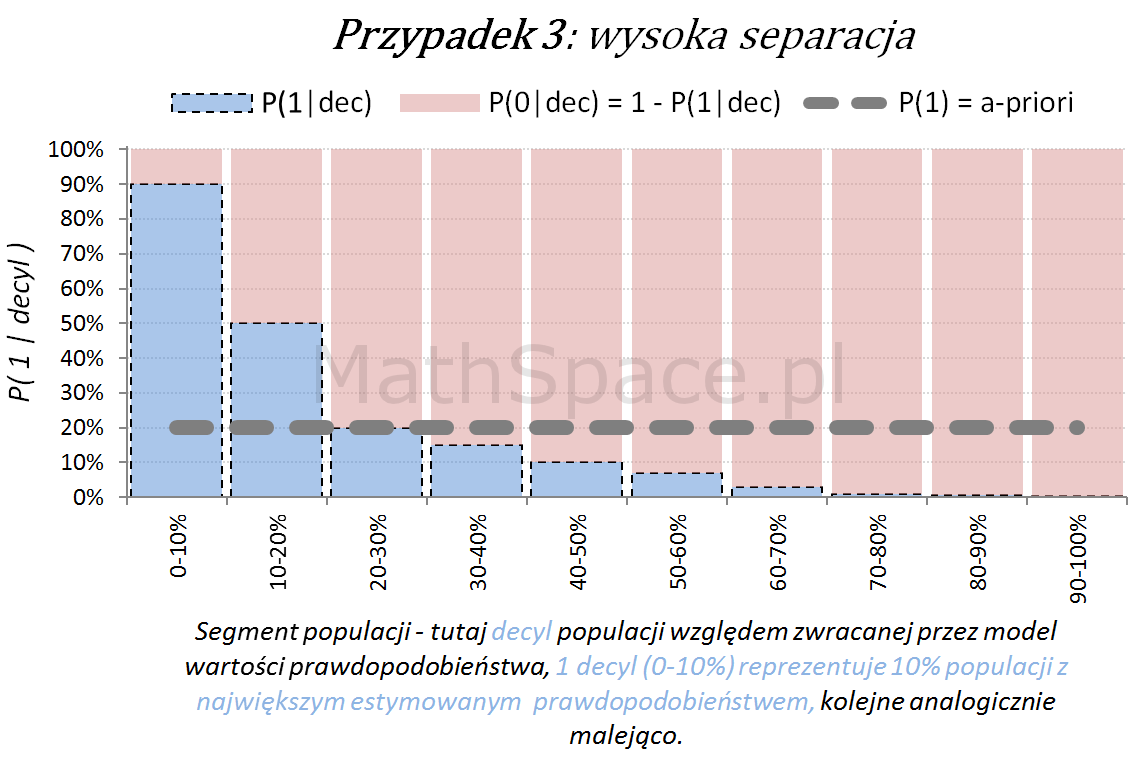
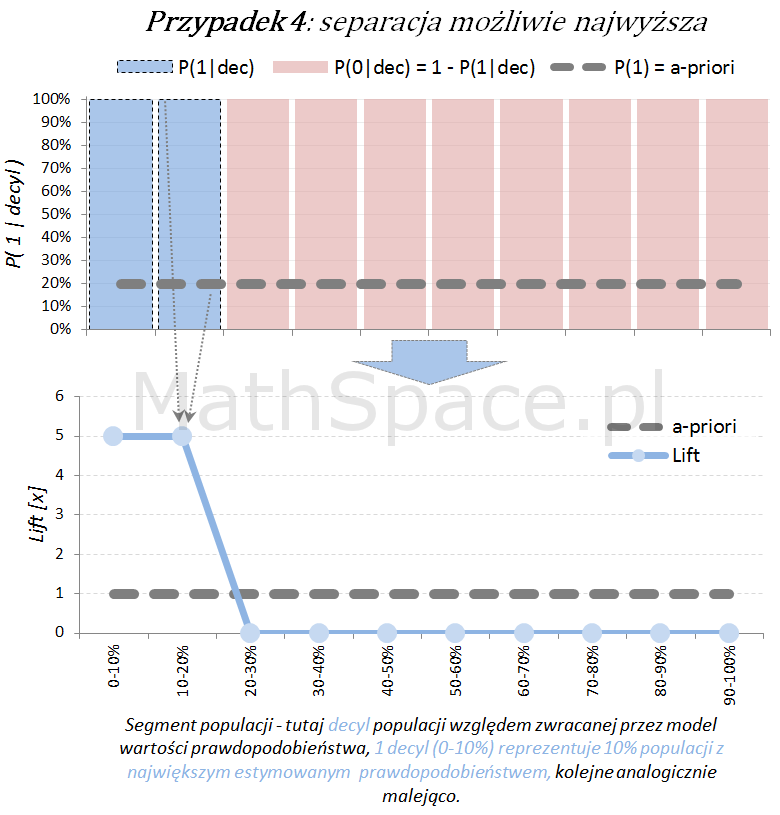
Dla każdego przypadku klasyfikacji istnieje również teoretyczny model idealny, z możliwie najwyższą siłą separacji klas. Tak model się „nie myli”, co obrazuje poniższy schemat.
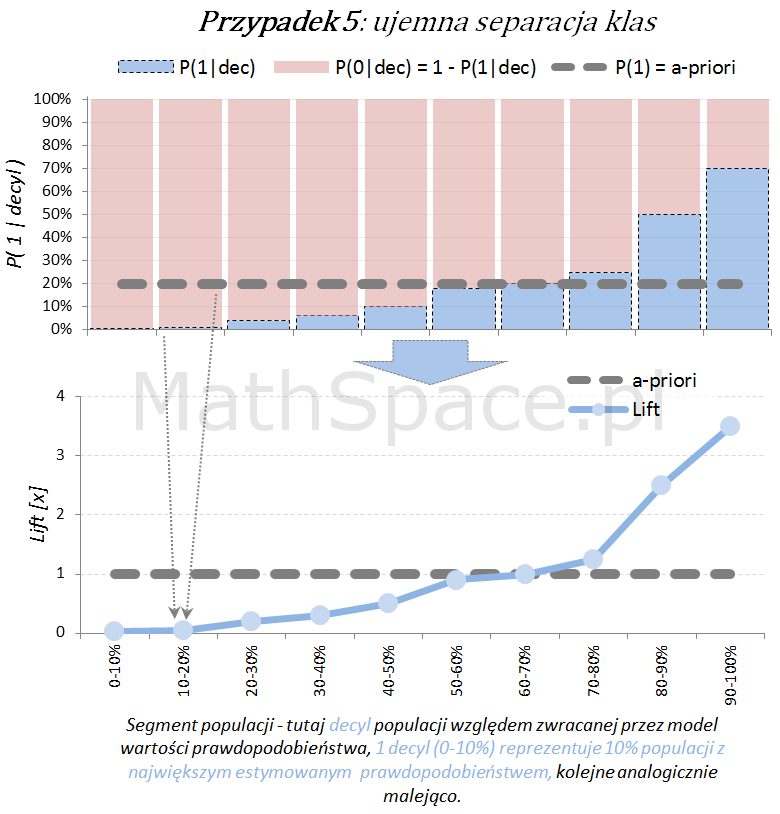
Inne „nietypowe” przypadki (jednak czasami spotykane w praktyce) to modele z ujemną korelacją w stosunku do targetu.
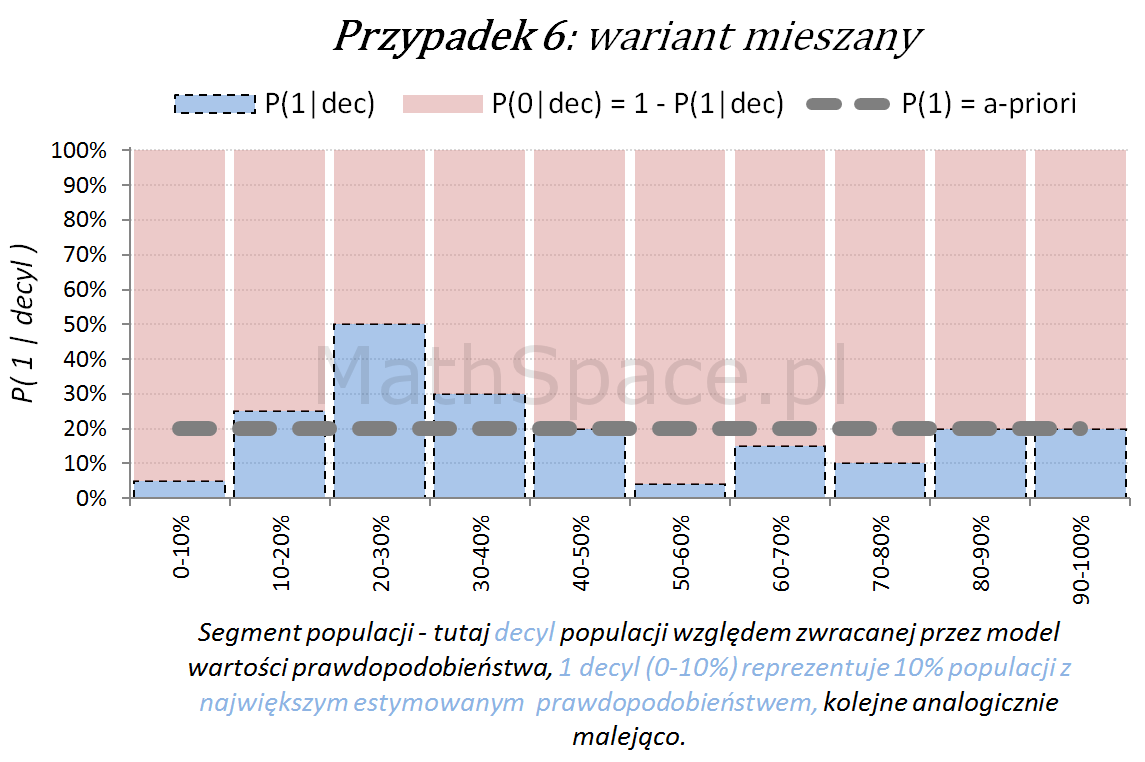
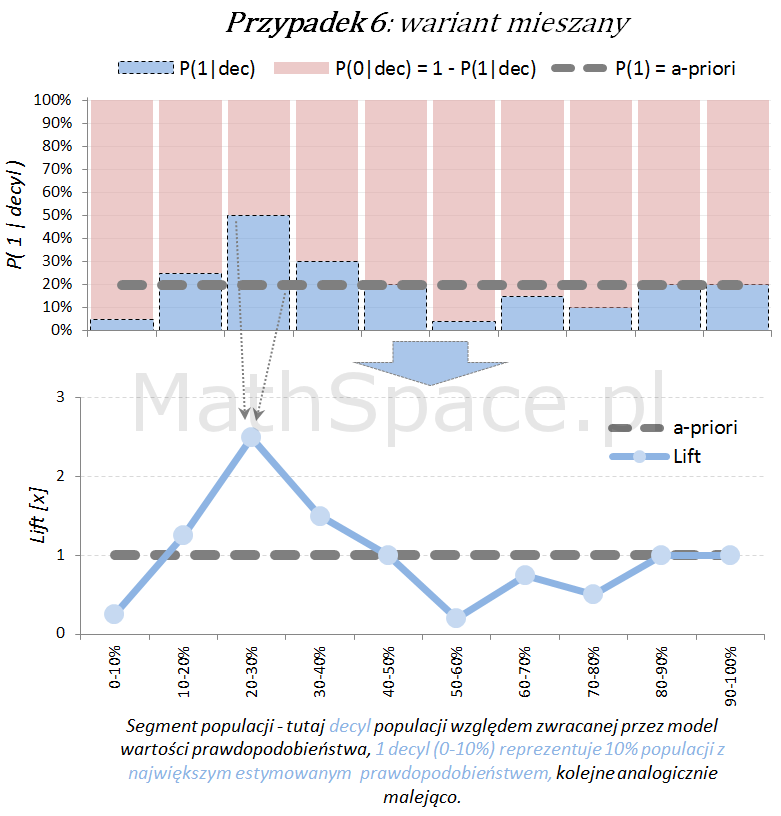
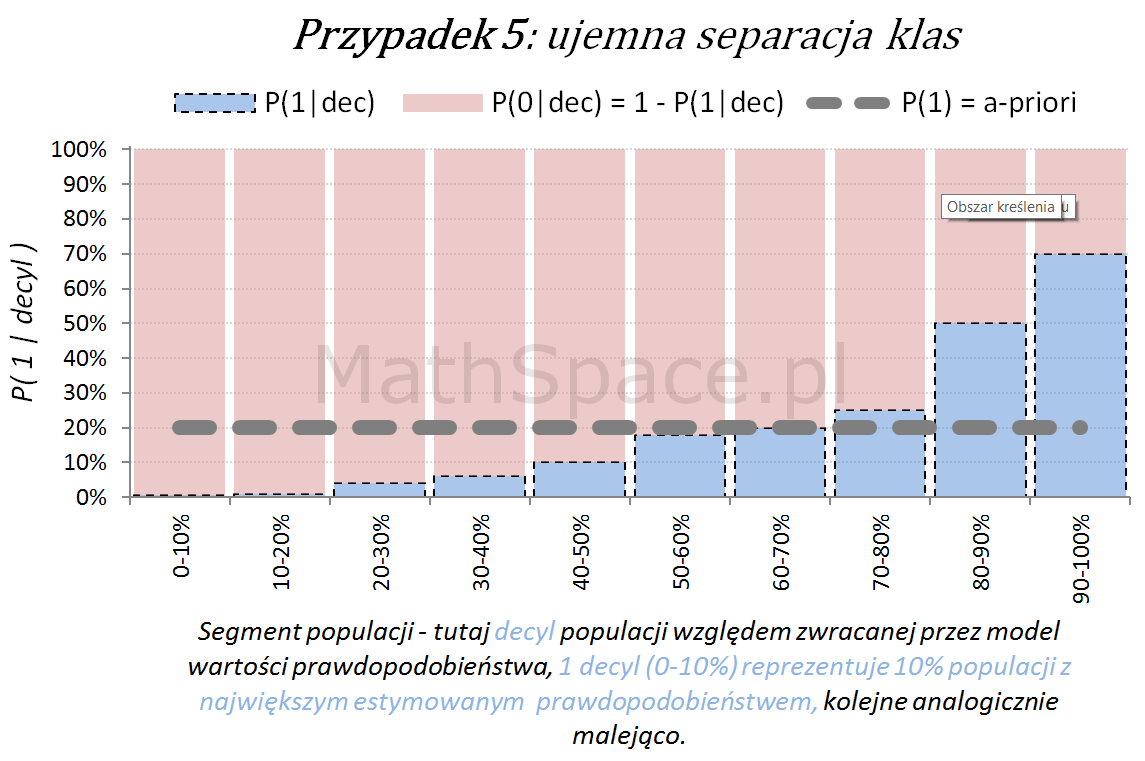Ostatecznie możliwy jest również wariant „mieszany”, obserwowany często po długim czasie wykorzystywania modelu, bez jego aktualizacji, w wyniku zmian w danych, błędów w danych, zmian definicji klas (tzw, targetu), itp.
Model predykcyjny a siła separacji klas – nieskumulowany lift
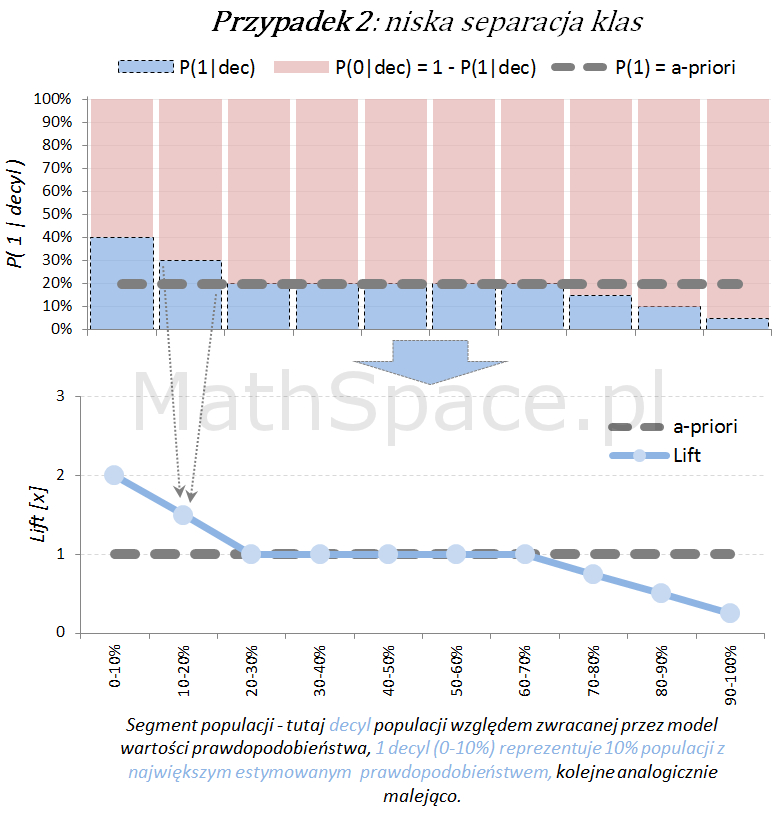
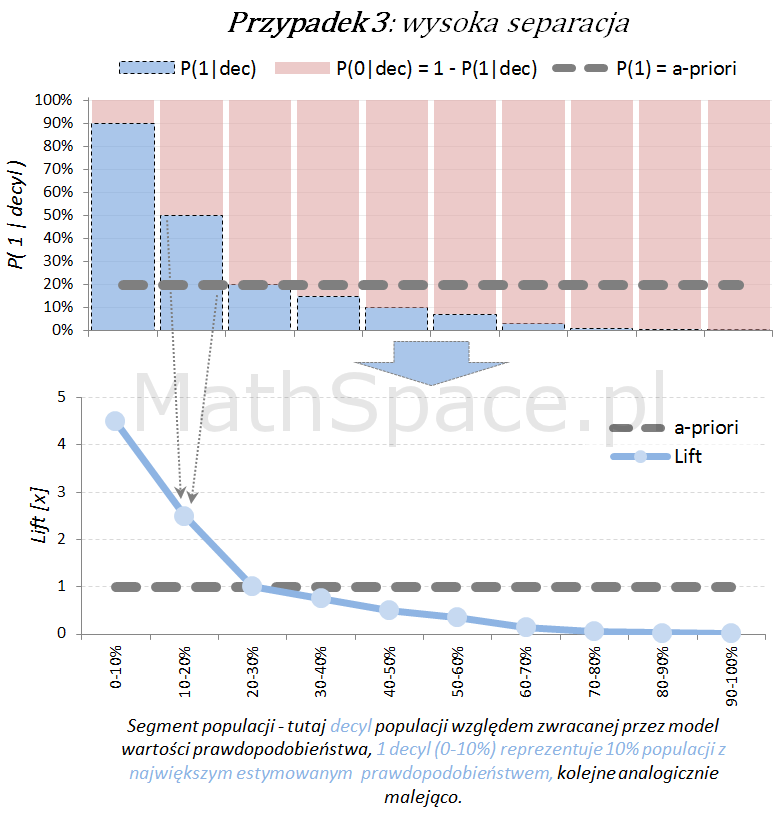
Lift jest normalizacją oceny prawdopodobieństwa do rozmiaru klasy pozytywnej, czyli do rozmiaru reprezentowanego przez prawdopodobieństwo a-priori $P(1)$. Lift powstaje przez podzielenie wartości prawdopodobieństwa właściwej dla segmentu przez prawdopodobieństwo a-priori. W ten sposób powstaje naturalna interpretacja liftu, jako krotności w stosunku do modelu losowego (czyli modeli bez separacji klas):
- lift < 1 – mniejsza częstość „klasy 1” niż średnio w populacji
- lift = 1 – częstość „klasy 1” na średnim poziomie dla populacji
- lift > 1 – większa częstość „klasy 1” niż średnio w populacji
Poniżej prezentacja graficzna
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
