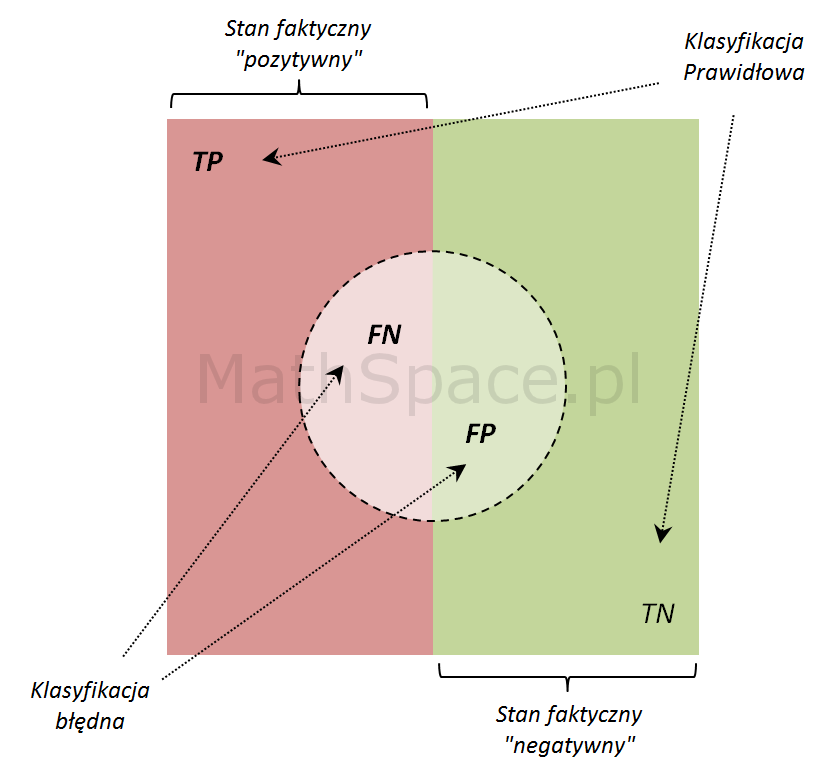
Wpis z dnia 26 października 2015 „Confusion matrix, Macierz błędu, tablica pomyłek – czyli ocena jakości klasyfikacji (część 1)” przedstawia wstęp do macierzy błędu i jej podstawowych zastosowań. Poniżej prezentujemy kolejne miary jakości klasyfikacji oparte na poznanej macierzy błędu. Przypomnijmy kodowanie klas:
- 1 – Positive
- 0 – Negative
oraz 4 możliwe wyniki przewidywań:
- True-Positive (TP – liczba przewidywań prawdziwie pozytywnych);
- True-Negative (TN – liczba przewidywań prawdziwie negatywnych);
- False-Positive (FP – liczba przewidywań fałszywie pozytywnych);
- False-Negative (FN – liczba przewidywań fałszywie negatywnych).
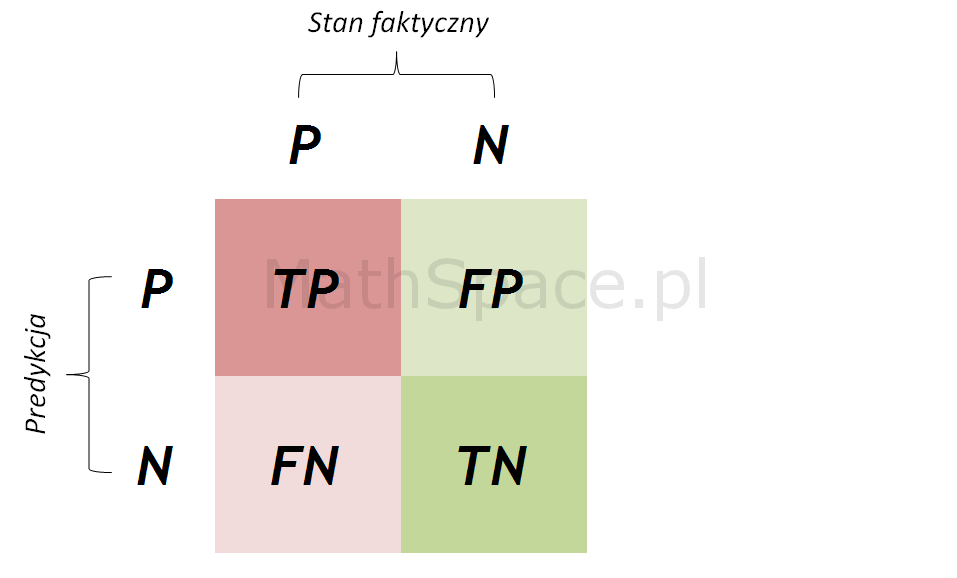
Czułość i specyficzność jako miary „zasięgu”
- Czułość = TPR = $\frac{TP}{TP+FN}$ – True-Positive Rate, miara „zasięgu / pokrycia / dotarcia” wskazująca w jakim procencie klasa faktycznie pozytywna została pokryta przewidywaniem pozytywnym (np. procent osób chorych, dla których test diagnostyczny wskazuje wynik pozytywny). TPR zapisujemy również jako
TPR = P( pred = P | fakt = P ) = P( pred = 1 | fakt = 1) = P( 1 | 1 )
- Specyficzność = TNR = $\frac{TN}{TN+FP}$ – True-Negative Rate, miara „zasięgu / pokrycia / dotarcia” wskazująca w jakim procencie klasa faktycznie negatywna została pokryta przewidywaniem negatywnym (np. procent osób zdrowych, dla których test diagnostyczny wskazuje wynik negatywny). TNR zapisujemy również jako
TNR = P( pred = N | fakt = N ) = P( pred = 0 | fakt = 0) = P( 0 | 0 )
PPV i NPV jako miary precyzji
- Precyzja przewidywania pozytywnego = PPV = $\frac{TP}{TP+FP}$ – Positive Predictive Value, miara precyzji wskazująca z jaką pewnością możemy ufać przewidywaniom pozytywnym, tzn. w jakim procencie przewidywania pozytywne potwierdzają się stanem faktycznie pozytywnym (np. procent osób z pozytywnym wynikiem testu medycznego, u których następnie potwierdzono diagnozę). PPV można zapisać również jako
PPV = P( fakt = P | pred = P) = P( fakt = 1 | pred = 1 )
- Precyzja przewidywania negatywnego = NPV = $\frac{TN}{TN+FN}$ – Negative Predictive Value, miara precyzji wskazująca z jaką pewnością możemy ufać przewidywaniom negatywnym, tzn. w jakim procencie przewidywania negatywne potwierdzają się stanem faktycznie negatywnym (np. procent osób z negatywnym wynikiem testu medycznego, u których następnie wykluczono chorobę). NPV można zapisać również jako
NPV = P( fakt = N | pred = N) = P( fakt = 0 | pred = 0 )
Miary zasięgu i precyzji na schemacie macierzy błędu
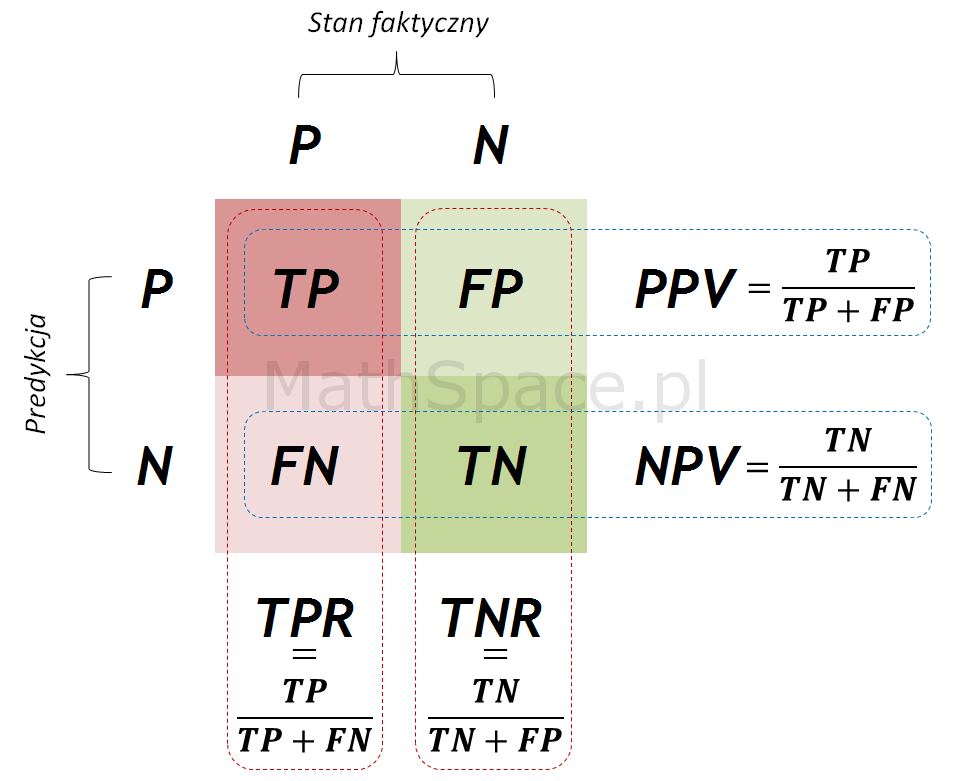
Miary zasięgu i precyzji na schemacie błędu klasyfikacyjnego
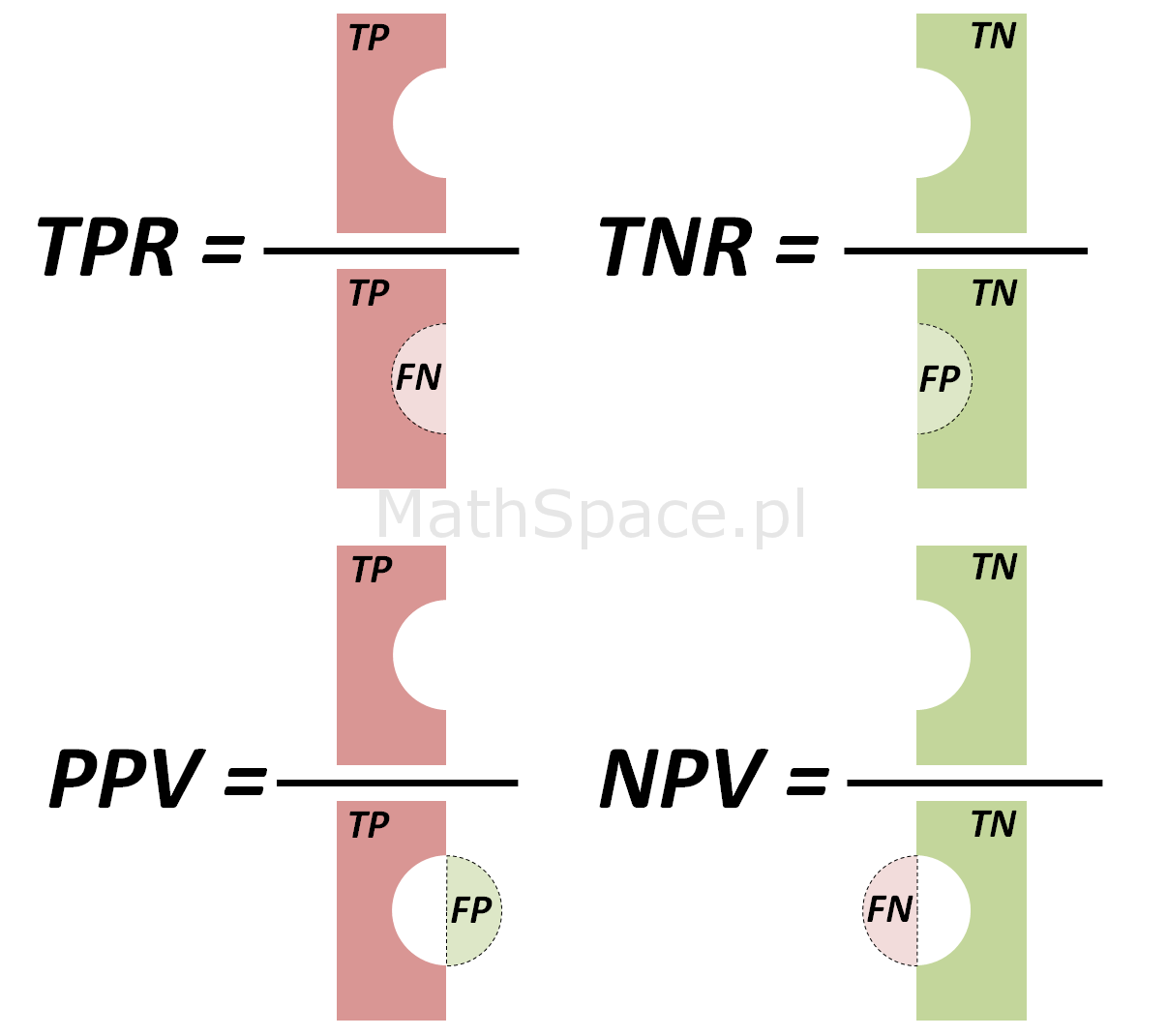
Zależność pomiędzy miarami jakości klasyfikacji
- Czułość (TPR) vs Specyficzność (TNR) – teoretycznie miary niezależne, co dobrze obrazują powyższe schematy. W praktyce jednak zwiększanie czułości prowadzi często do zmniejszenia specyficzności.
- PPV i NPV vs Czułość (TPR) vs Specyficzność (TNR) – korzystając z twierdzenia Bayesa można łatwo wyznaczyć zależność pomiędzy miarami precyzji i miarami zasięgu
$$\quad$$
$${\small PPV=P(fakt=1|pred=1)=}$$
$${\tiny=\frac{ P(fakt = 1) \cdot P(pred = 1 | fakt = 1) }{ P( fakt = 1)\cdot P( pred = 1 | fakt = 1) +P(fakt = 0) \cdot P(pred = 1 | fakt = 0)}=}$$
$${\small=\frac{ P(1) \cdot P(1 |1) }{ P(1)\cdot P(1|1) +P(0) \cdot P(1|0)}=}$$
$${\small=\frac{ P(1) \cdot P(1 |1) }{ P(1)\cdot P(1|1) +P(0) \cdot \big(1-P(0|0)\big)}=}$$
$${\small=\frac{ P(1) \cdot TPR}{ P(1)\cdot TPR+P(0) \cdot \big(1-TNR\big)}=}$$
$$\quad$$
$${\small NPV=P(fakt=0|pred=0)}$$
$${\tiny=\frac{ P(fakt = 0) \cdot P(pred = 0 | fakt = 0) }{ P( fakt = 0)\cdot P( pred = 0 | fakt = 0) +P(fakt = 1) \cdot P(pred = 0 | fakt = 1)}=}$$
$${\small=\frac{ P(0) \cdot P(0|0) }{ P(0)\cdot P(0|0) +P(1) \cdot P(0|1)}=}$$
$${\small=\frac{ P(0) \cdot P(0 |0) }{ P(0)\cdot P(0|0) +P(1) \cdot \big(1-P(1|1)\big)}=}$$
$${\small=\frac{ P(0) \cdot TNR}{ P(0)\cdot TNR+P(1) \cdot \big(1-TPR\big)}}$$
$$\quad$$
- PPV vs NPV – miary mocno od siebie zależą, np. zwiększając frakcję TP zmniejszamy frakcję FN, lub zmniejszając frakcję FP zwiększamy frakcję TN.
Ciąg dalszy nastąpi 🙂
- Confusion matrix, Macierz błędu, tablica pomyłek – czyli ocena jakości klasyfikacji (część 1)
- Model predykcyjny i punkt odcięcia (cut-off point) – czyli ocena jakości klasyfikacji (część 3)
- Model predykcyjny i siła separacji klas – czyli ocena jakości klasyfikacji (część 4)
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
