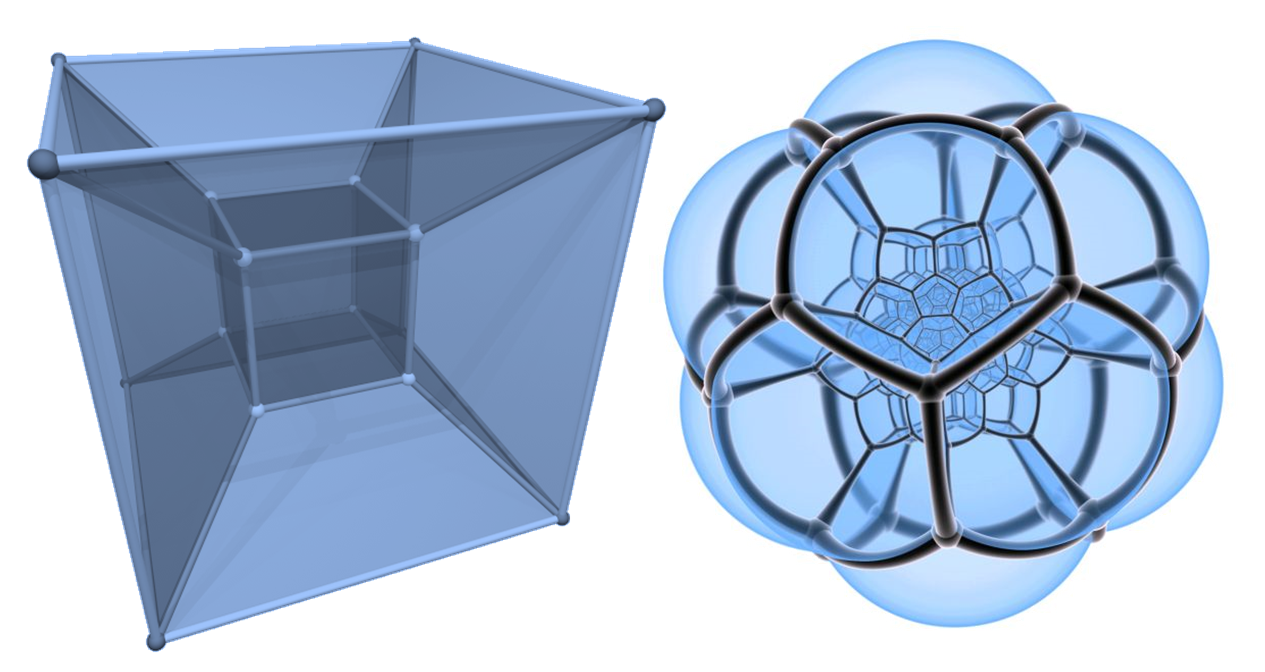
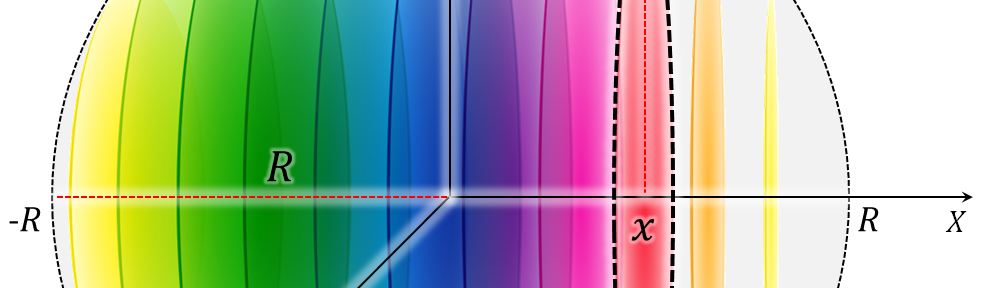
„Jak oczami wyobraźni zobaczyć 4 wymiary? – zapytano matematyka. To proste – odpowiedział – wystarczy wyobrazić sobie n-wymiarów i podstawić n=4″ 🙂 Dzisiejszy wpis poświęcę pomiarom odległości, powierzchni i pojemności w przestrzeniach wielowymiarowych. N-wymiarowa przestrzeń euklidesowa dostarcza dosyć oczywistą metrykę – a przez to wydawałoby się – bardzo intuicyjną. To wrażanie jest jednak mylne, co łatwo pokazać analizując wpływ zwiększania… Read More Egzotyczna hiperkula – czyli o pomiarach w przestrzeni wielowymiarowej