Pole powierzchni figur płaskich podobnych zmienia się z kwadratem skali podobieństwa – fakt nauczany już w szkole podstawowej. Dziś zadajemy pytanie „dlaczego” tak jest? O ile uzasadnienie dla najprostszych typów figur jest banalne (wynika bezpośrednio ze wzorów na pole), to w przypadku powierzchni ograniczonej dowolną krzywą (no może nie do końca dowolną) potrzeba już nieco więcej gimnastyki. Pokażę kilka podjeść, w tym osobno „pokryciowe”, osobno oparte na całce Riemanna, oraz osobno na bazie przekształcenia liniowego. Na koniec podam bardziej ogólne wnioski co do zmiany pola powierzchni względem znacznie szerszej niż podobieństwo klasy transformacji. Zapraszam 🙂

Czym jest podobieństwo?

Dwa obiekty geometryczne płaskie można nazwać podobnymi jeśli mają „ten sam kształt”. Powiemy nieco bardziej precyzyjnie (choć nadal nie dość bardzo), że dwie figury są podobne jeśli drugą można uzyskać z pierwszej poprzez zastosowanie dowolnej kombinacji poniższych transformacji:

• przesuwanie
• obracanie
• zmniejszanie
• zwiększanie
• symetryczne odbicie (np. lustrzane)

Warunek zachowania „tego samego kształtu” implikuje, że podobieństwo to  przekształcenie zachowujące stosunki odległości pomiędzy punktami.

Definicja precyzyjna: jeśli $\big(X,d\big)$ jest przestrzenią metryczną, a $k>0$ pewną stałą, to bijekcję

$$f:X\to X$$

spełniająca warunek

$$\displaystyle\forall_{x,y\in X}$$ $$~~$$ $$d(x,y)=k\cdot d(x^\prime,y^\prime)$$

gdzie

$$x^\prime=f(x)$$

$$y^\prime=f(y)$$

nazywamy podobieństwem o skali podobieństwa $k$.

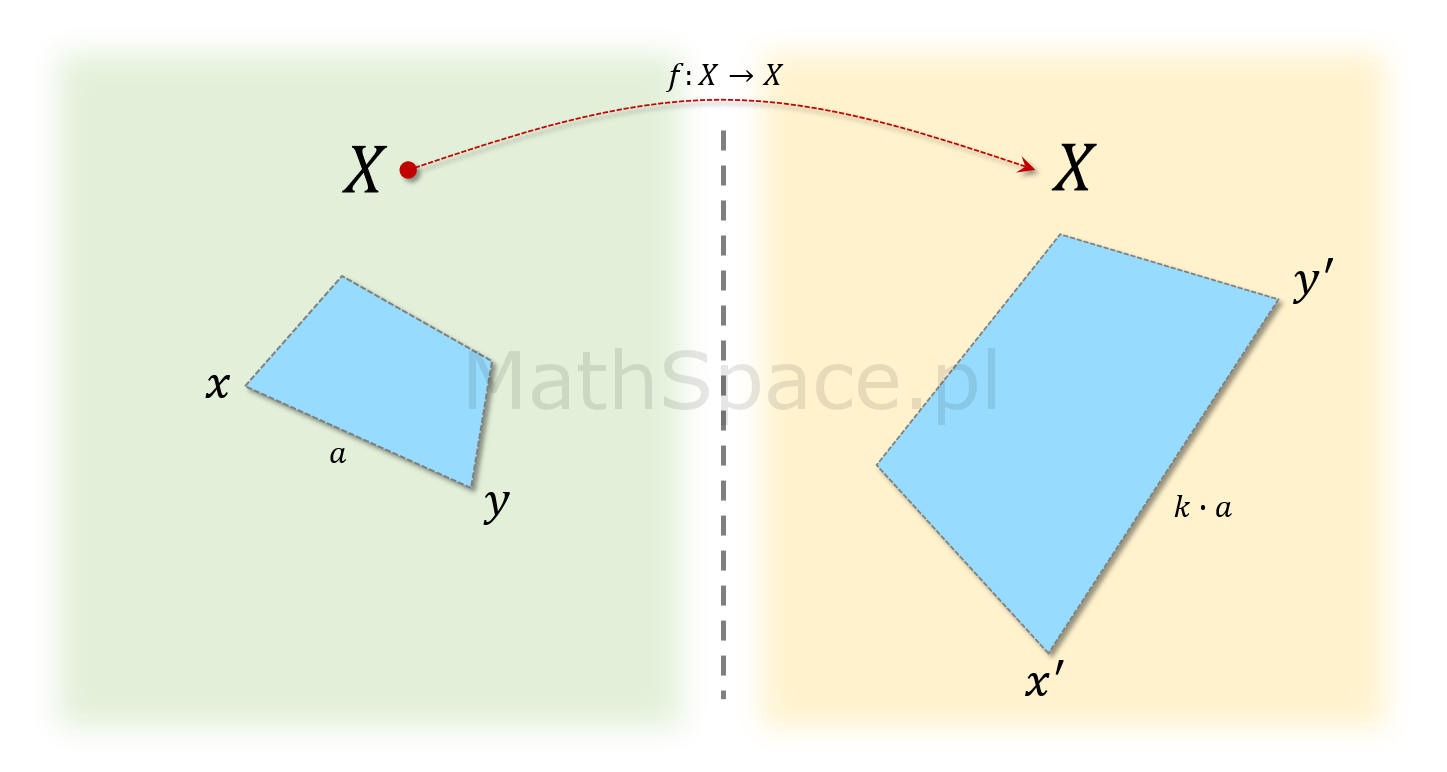
Skala podobieństwa to skala zmiany odległości pomiędzy punktami.

Pole powierzchni figur płaskich podobnych

Twierdzenie: jeśli pole powierzchni figury płaskiej wynosi $P$, to pole powierzchni figury do niej podobnej będzie wyrażone przez

$$P^\prime=k^2\cdot P$$

gdzie $k>0$ to skala podobieństwa.

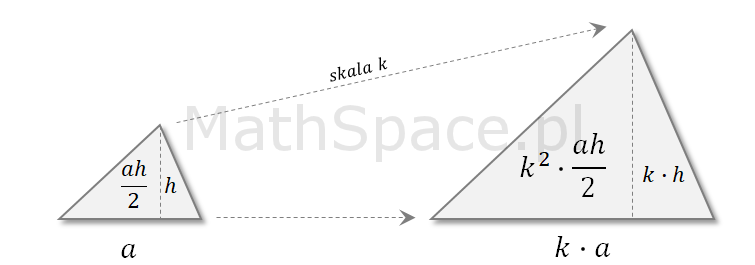
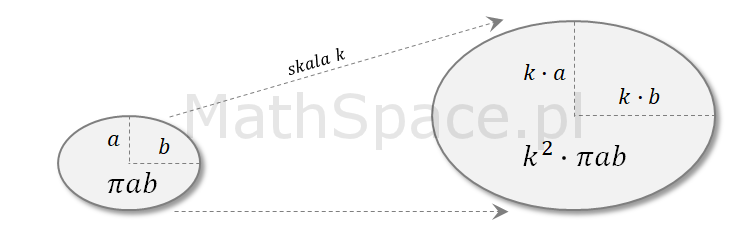
Jest to bardzo łatwe do wykazania dla kilku podstawowych typów figur płaskich poprzez bezpośrednie wykorzystanie wzorów na pola powierzchni.

Kwadrat

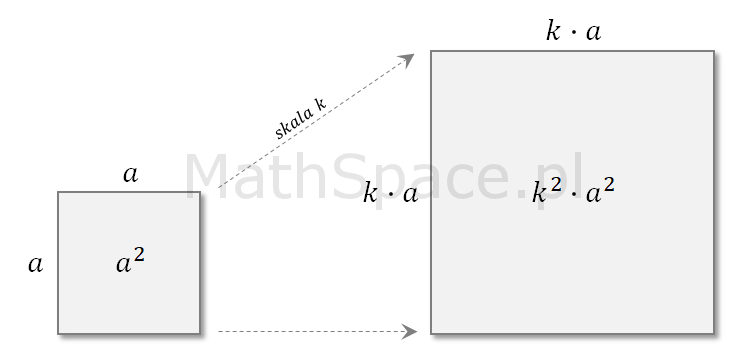
Prostokąt

Trójkąt

Koło

Elipsa

Wielokąt: poprzez podział na trójkąty

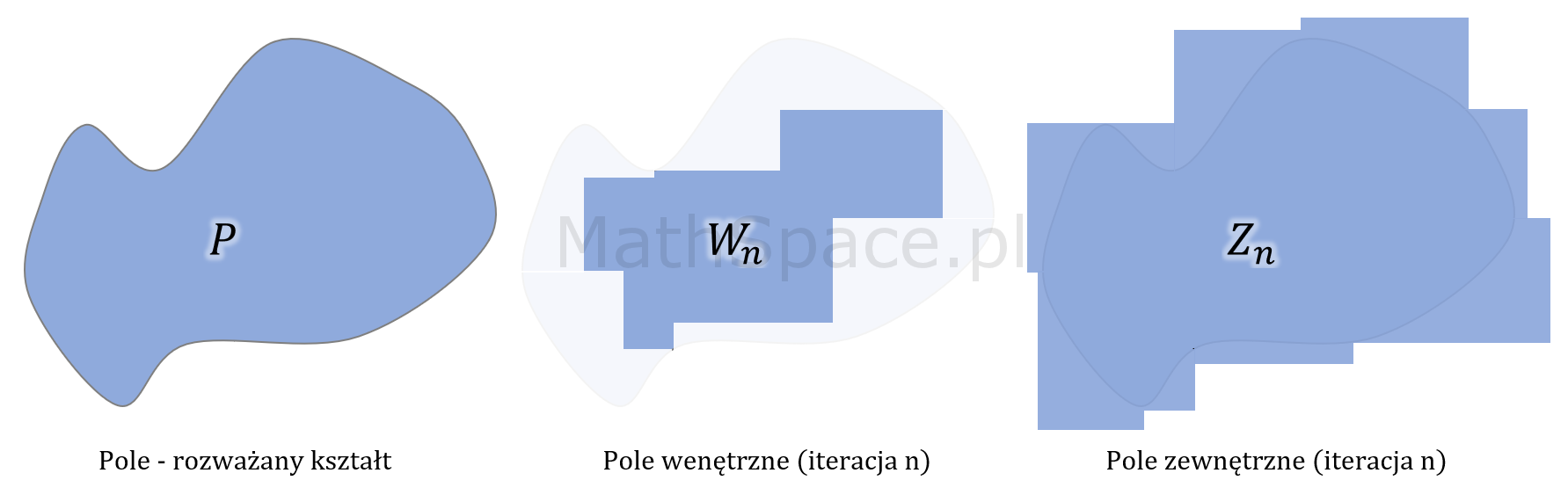
Pole powierzchni ograniczone dowolną krzywą

Koła, elipsy, wielokąty, czy też dowolne sumy tych trzech obiektów – to bardzo szeroka klasa kształtów, która podlega prawu zmiany pola powierzchni wraz z kwadratem skali podobieństwa. Rozsądek każe szukać uzasadnienia, że jest tak również dla dowolnych kształtów ograniczonych „normalnymi” krzywymi (pomijam zbiory niemierzalne i wszystkie inne nietrywialne struktury).

Uzasadnienie pokryciowe

Rozważmy dowolną krzywą zamkniętą ograniczającą pewną powierzchnię $P$, która posiada skończenie wiele „wypukłości” i „wklęsłości”.

Konstrukcja pokrycia

Ustalając orientację i oznaczając miejsca „wklęsłości” oraz „wypukłości” dzielimy krzywą na kawałki, które stanowią punkt wyjścia do wykonania „pewnego sprytnego” pokrycia krzywej.

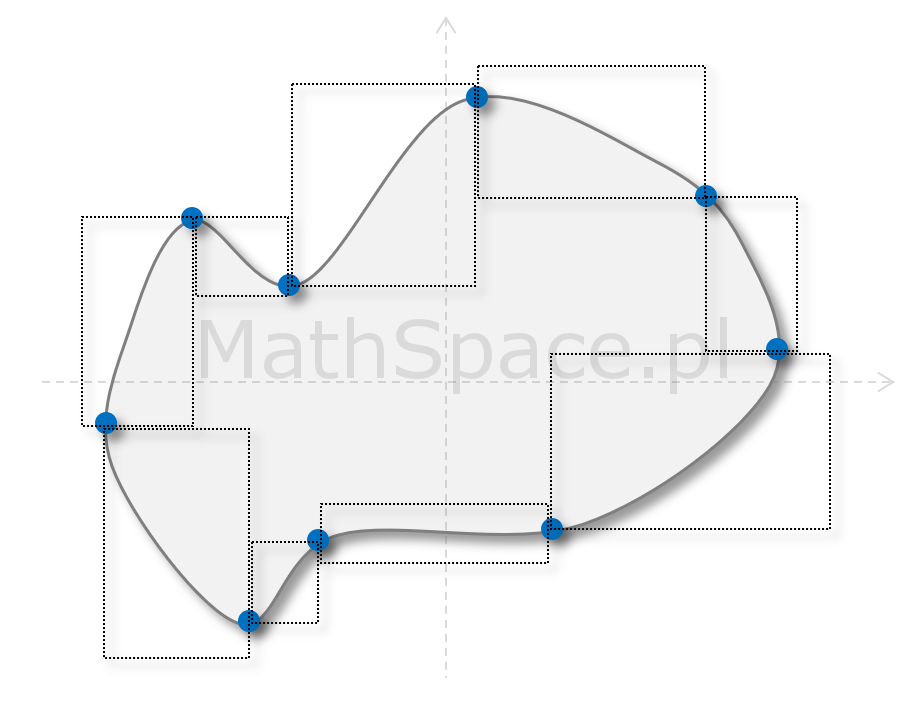
Pokrycia dokonujemy prostokątami w taki sposób, aby część „wewnątrz” była równa części leżącej poza rozważaną figurą. Dodatkowo procedura powinna być realizowana w orientacji narzuconej ustalonym układem współrzędnych (dzięki temu prostokąty nie mają części wspólnych). Możliwość wyboru takiego pokrycia gwarantuje odpowiedni podział krzywej. Rozważając wybrany „kawałek” początkowo wykreślamy taki prostokąt, aby końce „odcinka” stanowiły wierzchołki prostokąta leżące na jego przekątnej. Następnie tak przesuwamy jeden bok (modyfikując prostokąt), aby uzyskać równość pól „wewnątrz” i „na zewnątrz”. Równość pól nie jest niezbędna, pozwala natomiast wykonać dowód „w jednym przebiegu”.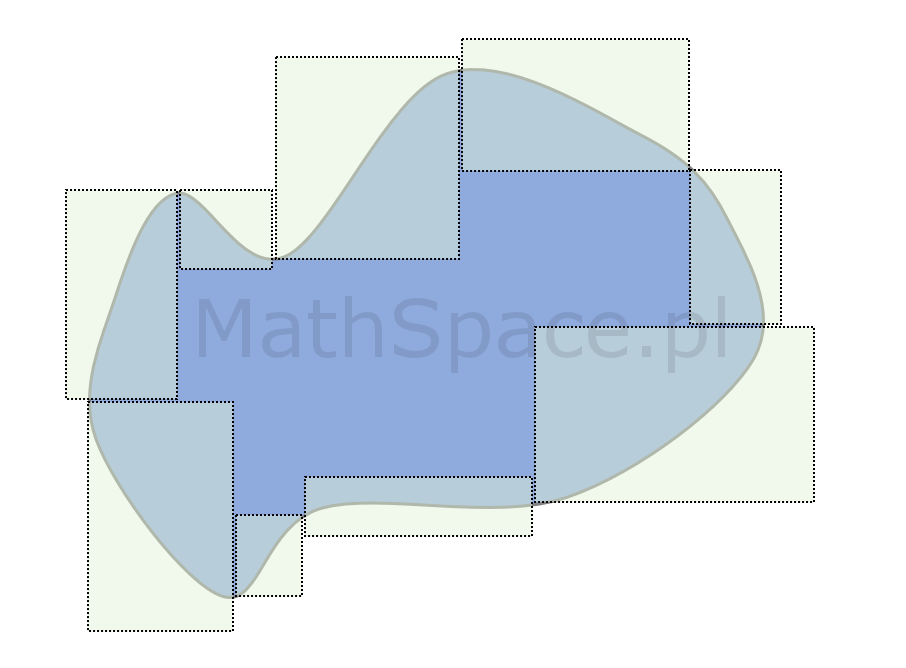

Uzyskaliśmy dwa kształty

• $W_n$ przybliżenie wyjściowej figury „od wewnątrz”
• $Z_n$ przybliżenie wyjściowej figury „od zewnątrz”

spełniające warunek

$$P-W_n=Z_n-P$$

Dodatkowo kształty $W_n$ i $Z_n$ są wielokątami, zatem ich pole skaluje się z kwadratem skali podobieństwa.

$$W_n^\prime=k^2\cdot W_n$$

$$Z_n^\prime=k^2\cdot Z_n$$

Zbieżność ciągów $W_n$ oraz $Z_n$

Dzieląc części krzywej na kolejne jeszcze mniejsze coraz bardziej przybliżamy wyjściową figurę. Można łatwo pokazać „na epsilonach” (definicja zbieżności ciągu względem Cauchy’ego), że $W_n\to P$ oraz $Z_n\to P$.

Ustalamy $\epsilon>0$, dla tej wartości znajdujemy takie $N_\epsilon$ (dokonując coraz to „gęstszych” podziałów wszystkich „części” krzywej), że

$$P-W_{N_\epsilon}>\epsilon$$

$$Z_{N_\epsilon}-P>\epsilon$$

Jeśli zwiększymy „gęstość” jeszcze bardziej, tzn. $n>N_\epsilon$, wtedy

$$P>W_n>W_{N_\epsilon}$$

$$Z_{N_\epsilon}>Z_n>P$$

oraz

$$P-W_n>\epsilon$$

$$Z_n-P>\epsilon$$

ostatecznie (z definicji granicy ciągu względem Cauchy’ego) otrzymujemy

$$\lim_{n\to\infty}W_n=\lim_{n\to\infty}Z_n=P$$

Ostatnia faza dowodu

$$W_n^\prime=k^2\cdot W_n>P^\prime$$

$$P^\prime<Z_n^\prime=k^2\cdot Z_n$$

$W_n$ i $Z_n$ są zbieżne, zatem zbieżne są $W_n^\prime$ oraz $Z_n^\prime$.

$$\lim_{n\to\infty}W_n^\prime=k^2\cdot\lim_{n\to\infty}W_n=k^2\cdot P$$

$$\lim_{n\to\infty}Z_n^\prime=k^2\cdot\lim_{n\to\infty}Z_n=k^2\cdot P$$

oraz

$$\lim_{n\to\infty}Z_n^\prime\geq P^\prime\geq\lim_{n\to\infty}W_n^\prime$$

zatem

$$\lim_{n\to\infty}W_n^\prime=\lim_{n\to\infty}Z_n^\prime=P^\prime$$

ostatecznie

$$P^\prime=k^2\cdot P$$

Uzasadnienie na bazie całki

Całka Riemanna powstaje na zasadzie konstrukcji odpowiedniego pokrycia górnego i dolnego, więc to uzasadnienie ma wiele wspólnego z wcześniej opisanym. Cały sposób polega na tym, aby obszar ograniczony przez krzywą podzielić na kilka części: wielokąt (środek) + pola powierzchni pod funkcjami.

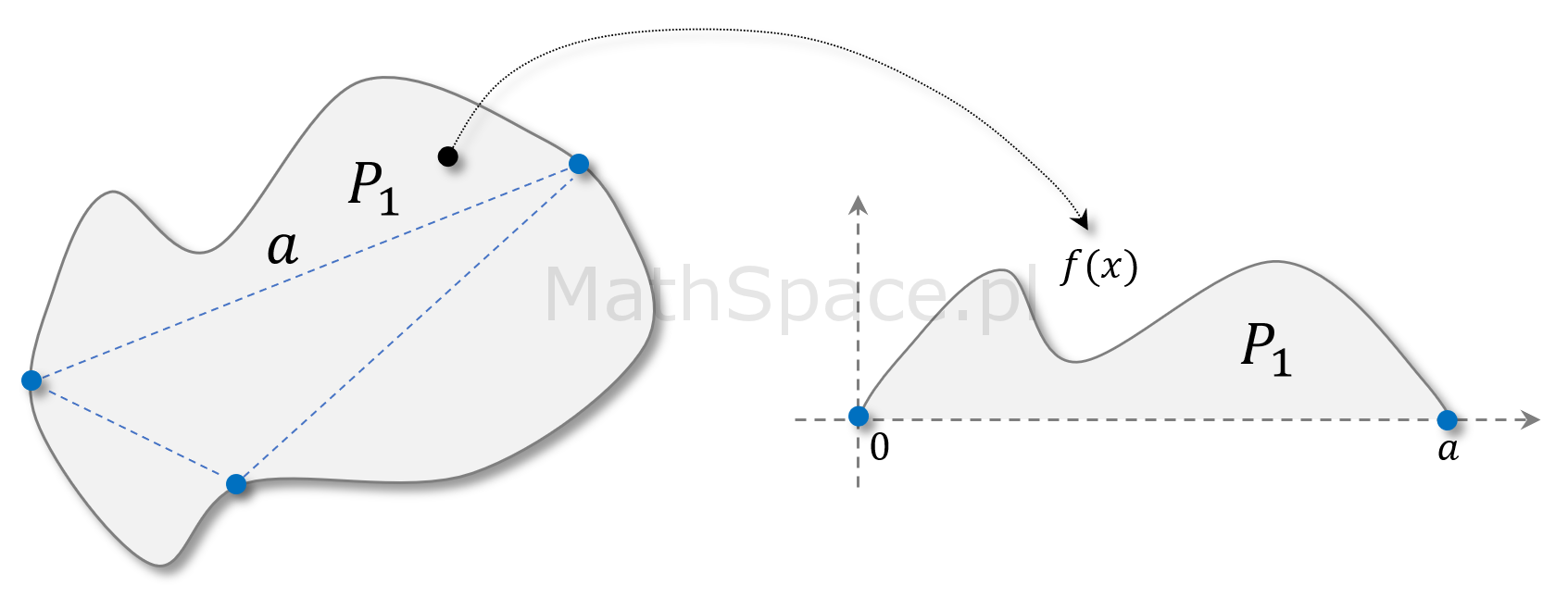
$$P_1=\displaystyle\int_0^af(x)dx$$

Bez utraty ogólności rozważań skupiamy się na przypadku $P_1$ – tzn. skalujemy go skalą k.

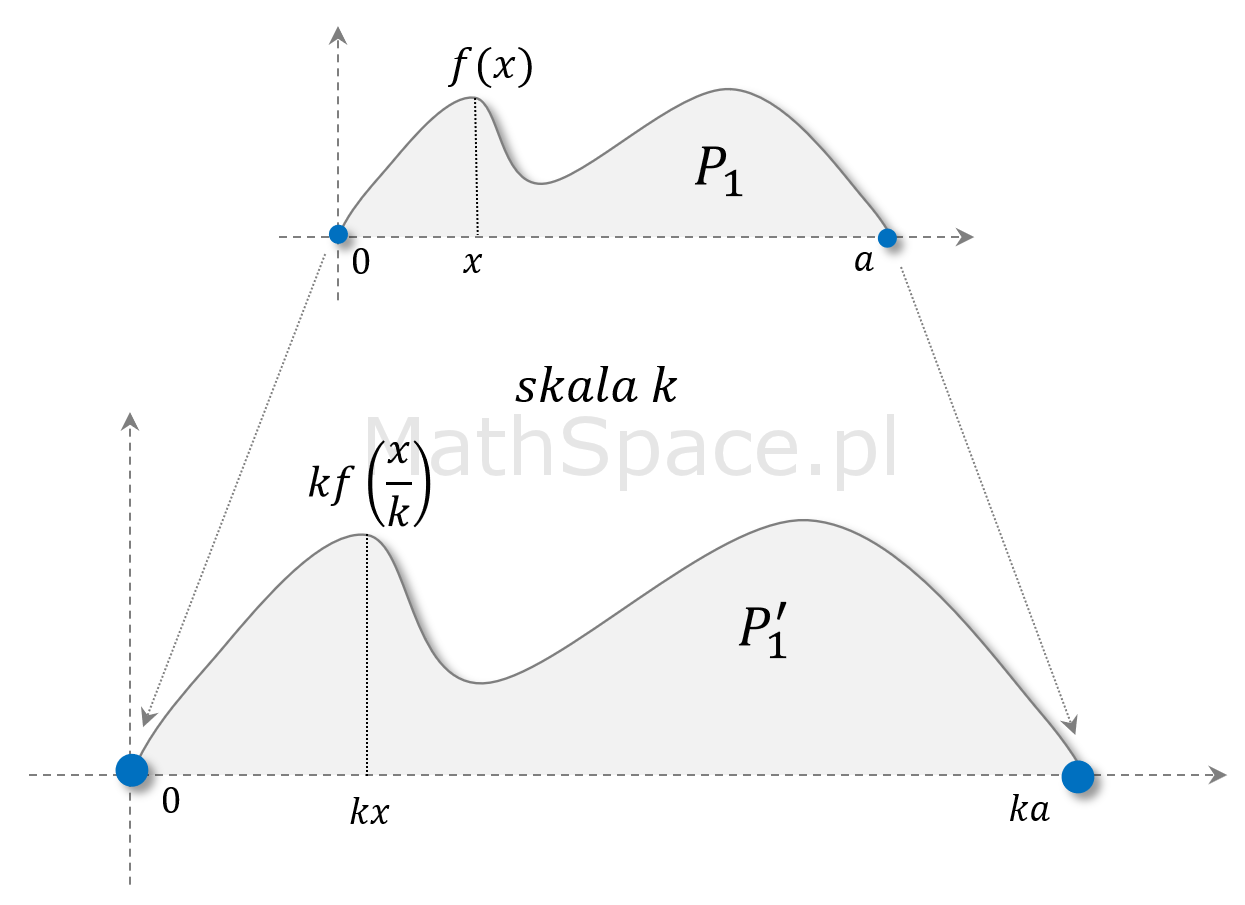
$$P_1^\prime=\displaystyle\int_0^{ka}kf\Big(\frac{x}{k}\Big)dx=\displaystyle\int_0^{ka}f\Big(\frac{x}{k}\Big)k^2\frac{dx}{k}=$$

$$=\begin{bmatrix}t=\frac{x}{k}\\dt=\frac{dx}{k}\\x=0\Rightarrow t=0\\x=ka\Rightarrow t=a\end{bmatrix}=$$

$$=\displaystyle\int_0^{a}k^2f(t)dt=k^2\cdot P_1$$

ostatecznie

$$P_1^\prime=k^2\cdot P_1$$

Uzasadnienie na bazie przekształcenia liniowego

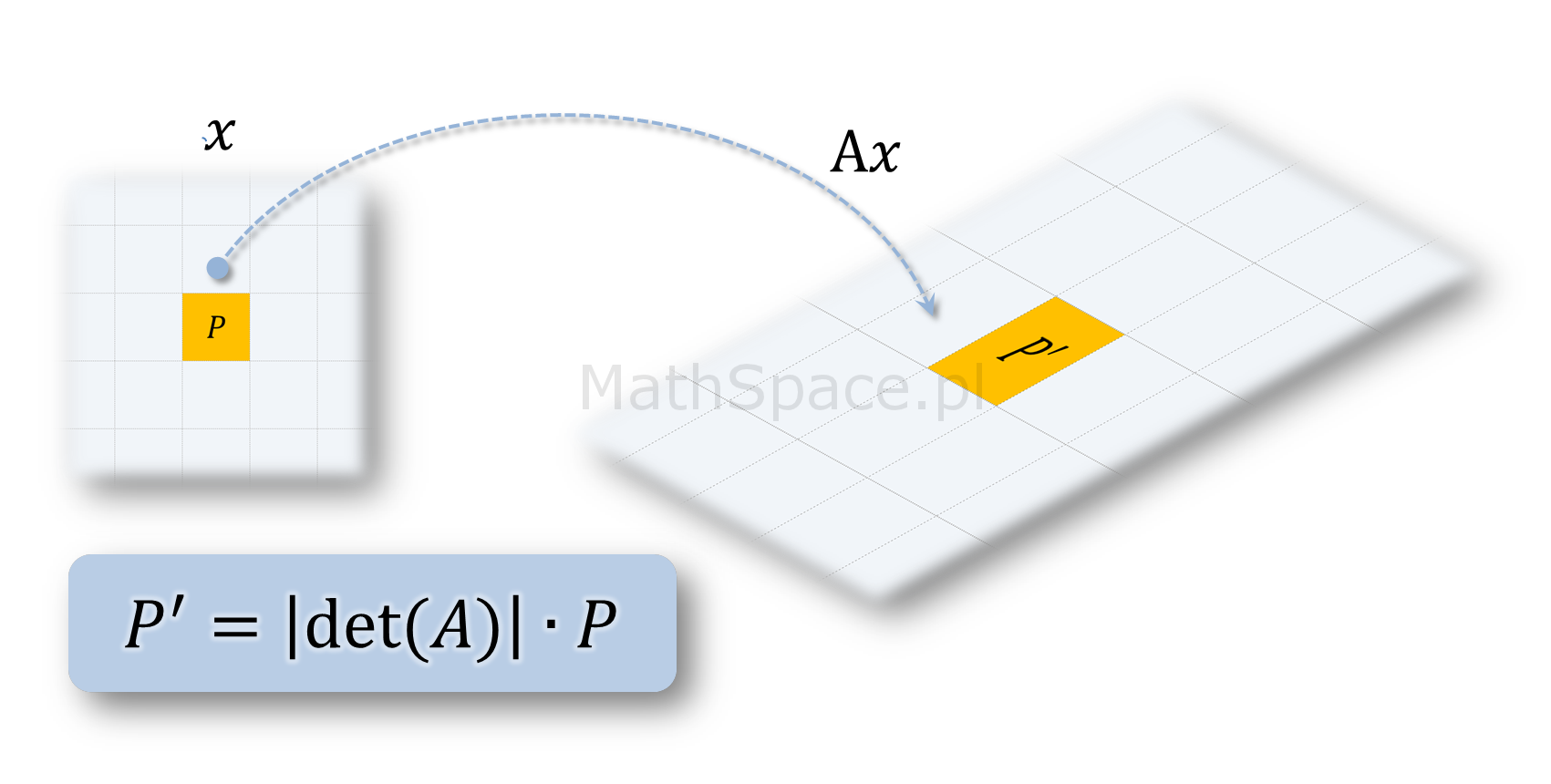
Jeśli analizujemy przekształcenie liniowe

$$Ax$$

gdzie $A$ jest macierzą przekształcenia liniowego, a $x$ wektorem, to wyznacznik

$$\text{det}(A)$$

jest współczynnikiem o jaki zmienia się pole powierzchni / objętość / miara figury / obiektu transformowanego poprzez przekształcenie liniowe $Ax$. Polecam poniższy film.

Niech

$$A=\begin{bmatrix}k && 0\\0 && k\end{bmatrix}$$

oraz

$\textbf{x}_1=\begin{bmatrix}x_1\\y_1\end{bmatrix}$ $~~$ $\textbf{x}_2=\begin{bmatrix}x_2\\y_2\end{bmatrix}$

$\textbf{x}_1^\prime=A\textbf{x}_1$ $~~$ $\textbf{x}_2^\prime=A\textbf{x}_2$

wtedy

$$\textbf{x}_1^\prime=\begin{bmatrix}k && 0\\0 && k\end{bmatrix}\cdot\begin{bmatrix}x_1\\y_1\end{bmatrix}=\begin{bmatrix}kx_1\\ky_1\end{bmatrix}$$

$$\textbf{x}_2^\prime=\begin{bmatrix}k && 0\\0 && k\end{bmatrix}\cdot\begin{bmatrix}x_2\\y_2\end{bmatrix}=\begin{bmatrix}kx_2\\ky_2\end{bmatrix}$$

$$d(\textbf{x}_1,\textbf{x}_2)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$

$$d(\textbf{x}_1^\prime,\textbf{x}_2^\prime)=\sqrt{(kx_2-kx_1)^2+(ky_2-ky_1)^2}=$$

$$=\sqrt{k^2(x_2-x_1)^2+k^2(y_2-y_1)^2}=$$

$$=\sqrt{k^2\Big[(x_2-x_1)^2+(y_2-y_1)^2\Big]}=$$

$$=k\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=kd(\textbf{x}_1,\textbf{x}_2)$$

Zatem $Ax$ jest podobieństwem.

$$\text{det}(A)=k^2-0=k^2$$

$$P^\prime=\big|\text{det}(A)\big|\cdot P=k^2\cdot P$$

🙂

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa