Jakiś czas temu rozważałem problem losowania ze zwracaniem dokładnie $n$-elementów z $n$-elementowego zbioru (dla uściślenia w zbiorze wyjściowym znajduje się dokładnie $n$ różnych elementów). W wyniku takiej operacji, w wylosowanej próbie, mogą pojawić się duplikaty - załóżmy zatem, że otrzymaliśmy $k$ unikalnych rezultatów (oczywiście $1\leq k\leq n$). Naturalnie pojawia się pytanie kombinatoryczne.

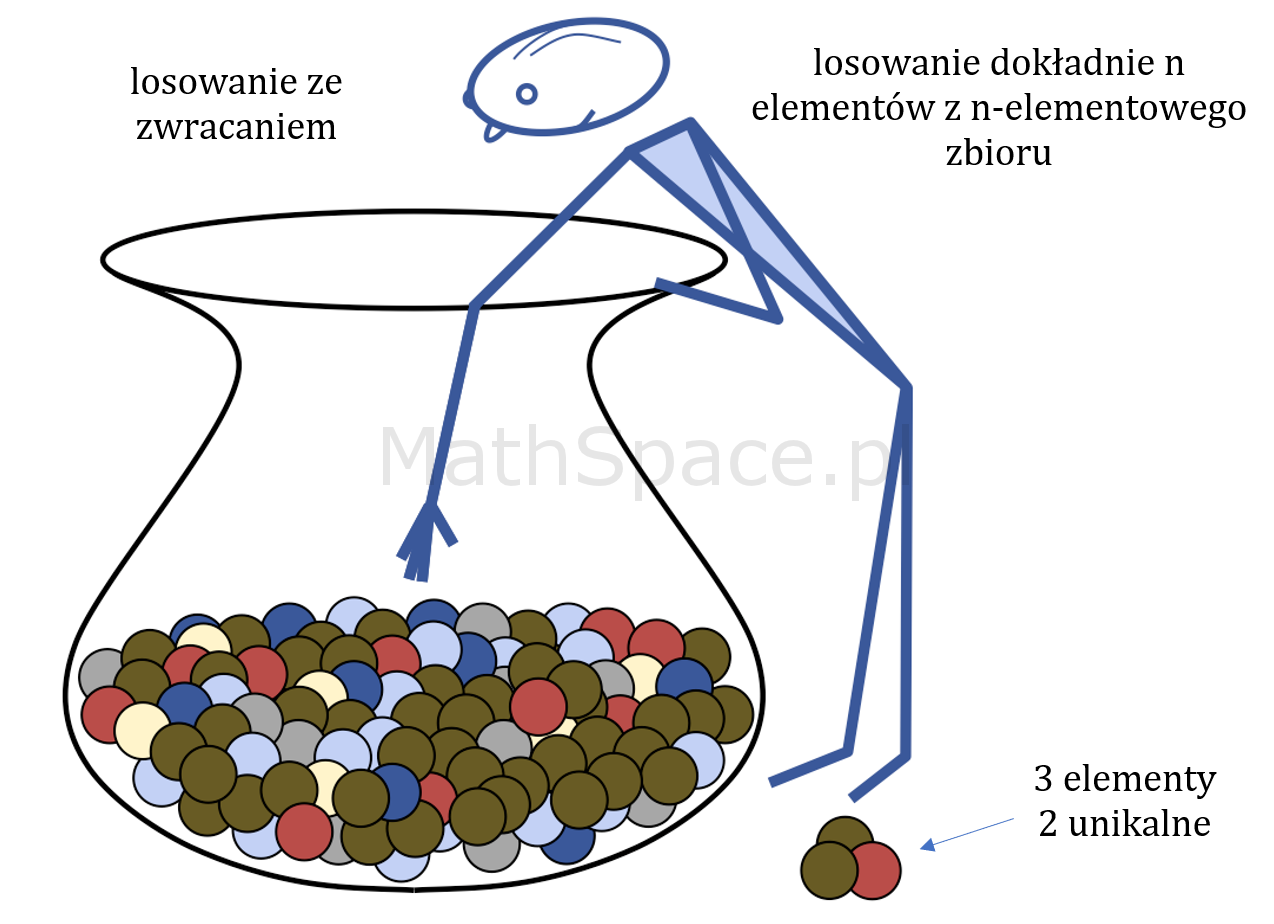
Ile istnieje sposobów takiego wylosowania (ze zwracaniem) $n$ elementów spośród $n$-elementowego zbioru, że w wyniku otrzymamy dokładnie $k$ unikalnych rezultatów?

Liczba sposobów otrzymania k-unikalnych rezultatów

Liczbę takich sposobów oznaczmy przez $B_n^k$.

"Kombinowanie" czas start! Początkowo wyszedłem od losowania $k$ różnych elementów, w kolejnym kroku planując losowanie $n-k$ z wylosowanych wcześniej $k$. Tego typu podejście prowadziło do bardzo skomplikowanych rozważań, szczegóły pominę. Na rozwiązanie wpadłem po około 2 dniach.

Wariacja bez powtórzeń

Pierwszy krok - liczba sposobów wyboru $k$ różnych elementów z $n$ zwracając uwagę na kolejność - jest to wariacja bez powtórzeń $V_n^k$.

$V_n^k=\frac{n!}{(n-k)!}$

Liczba Stirlinga II rodzaju

Drugi krok - zapominamy, że właśnie wylosowaliśmy $k$ unikalnych i należy jeszcze dolosować $n-k$ (choć to prawda). W zamian ustalamy, że mamy już $n$, w tym $k$ unikalnych. Trick polega na zauważeniu, że mając $k$ różnych elementów w zbiorze $n$-elementowym, dokonaliśmy jego podziału na $k$-podzbiorów.

Ile mamy sposobów podziału $n$-elementowego zbioru na $k$ podzbiorów? Jest to właśnie liczba Stirlinga II rodzaju oznaczona $S_2(n,k)$. Zatem finalnie

$B_n^k = V_n^k\cdot S_2(n,k)$

$S_2(n,k)=\begin{cases}kS_2(n-1,k)+S_2(n-1,k-1)\quad\text{dla}~k<n\\S_2(n,1)=1\\S_2(n,n)=1\\S_2(n,0)=0\\S_2(0,0)=1\\S_2(n,k)=0\quad\text{dla}~k>n\end{cases}$

Dlaczego w kroku pierwszym zwracałem uwagę na kolejność? Chętnych zapraszam do komentowania 🙂

Pozdrowienia,

Mariusz Gromada