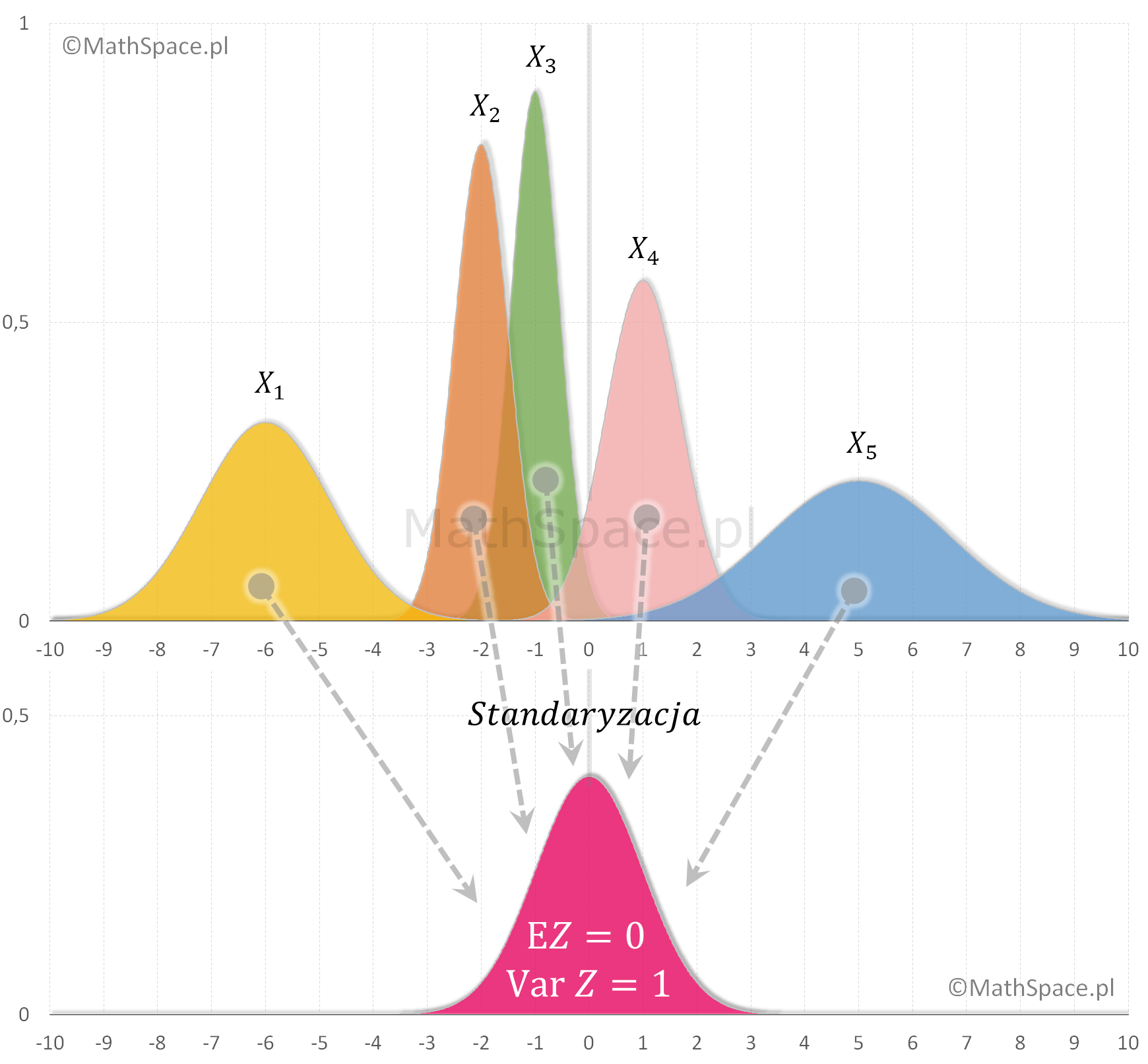
Standaryzacja zmiennej losowej $X$ to proces jej „normalizacji”, którego wynikiem jest taka zmienna losowa $Z$, że

$$\text{E}Z=0$$

$$\text{Var}(Z)=1$$

Standaryzację łatwo wyobrazić sobie jako działanie, które obywa się w dwóch krokach:

1. adekwatne „przesunięcie” zmiennej – tu chodzi o uzyskanie zerowej miary położenia, którą jest wartość oczekiwana (wartość średnia) zmiennej
2. odpowiednia „zmiana skali wartości” zmiennej – w tym przypadku „poprawiamy” miarę rozproszenia, którą jest wariancja.

Standaryzacja Z: jeśli X jest taką zmienną losową, że

$$\text{E}X=\mu$$

$$\text{Var}(X)=\sigma^2$$

to standaryzacją „Z” zmiennej losowej $X$ nazywamy zmienną

$$Z=\frac{X-\mu}{\sigma}$$

Uzasadnienie: z własności wartości oczekiwanej (funkcja liniowa)

$$\text{E}\big(a\cdot X+b\big)=a\cdot\text{E}X+b$$

$a, b$ – stałe

oraz własności wariancji, która „nie reaguje na przesunięcia” oraz „skaluje się z kwadratem skali podobieństwa” (na marginesie – taka analogia geometryczna do pola powierzchni figury)

$$\text{Var}\big(X+b\big)=\text{Var}\big(X\big)$$

$$\text{Var}\big(a\cdot X\big)=a^2\cdot\text{Var}\big(X\big)$$

$a, b$ – stałe

otrzymujemy

$$\text{E}Z=\text{E}\Big(\frac{X-\mu}{\sigma}\Big)=\frac{1}{\sigma}\Big(\text{E}X-\mu\Big)=$$

$$=\frac{1}{\sigma}\Big(\mu-\mu\Big)=\frac{1}{\sigma}\cdot 0=0$$

$$\text{Var}Z=\text{Var}\Big(\frac{X-\mu}{\sigma}\Big)=\Big(\frac{1}{\sigma}\Big)^2\text{Var}\big(X-\mu\big)=$$

$$=\frac{1}{\sigma^2}\text{Var}(X)=\frac{1}{\sigma^2}\cdot\sigma^2=1$$

W literaturze powszechna jest postać standaryzowanej zmiennej losowej, natomiast nieco trudniej odnaleźć (mi się nie udało – ale krótko szukałem) wzory na standaryzowaną gęstość, standaryzowaną dystrybuantę, standaryzowaną odwrotną dystrybuanty. Właśnie ta trudność jest motywacją dzisiejszego wpisu.

Standaryzacja funkcji gęstości zmiennej losowej

Założenia

• $X$ – zmienna losowa z ciągłego rozkładu
• $\text{E}X=\mu$ – znane
• $\text{Var}(X)=\sigma^2$ – znane
• $f(x)$ – gęstość rozkładu – znana

Poszukujemy nowej gęstości rozkładu prawdopodobieństwa

$$f_Z(x)=af(bx+c)$$

Zaczynamy od warunku na gęstość – tzn. „masa prawdopodobieństwa” to 1.

$$\displaystyle\int_\mathbb{R}f_Z(x)dx=1$$

$$\displaystyle\int_\mathbb{R}f_Z(x)dx=\displaystyle\int_\mathbb{R}af(bx+c)dx=$$

$$=\begin{bmatrix}t=bx+c\\\frac{dt}{b}=dx\end{bmatrix}=$$

$$=\displaystyle\int_\mathbb{R}af(t)\frac{dt}{b}=\frac{a}{b}\displaystyle\int_\mathbb{R}f(t)dt=\frac{a}{b}\cdot 1$$

$\frac{a}{b}=1$ zatem $a=b$

Zapisujemy

$$f_Z(x)=af(ax+c)$$

Stosujemy warunek na wartość oczekiwaną równą „0”

$$0=\displaystyle\int_\mathbb{R}xf_Z(x)dx=\displaystyle\int_\mathbb{R}xaf(ax+c)dx=$$

$$=\begin{bmatrix}t=ax+c\\\frac{dt}{a}=dx\\x=\frac{t-c}{a}\end{bmatrix}=$$

$$=\displaystyle\int_\mathbb{R}\frac{t-c}{a}af(t)\frac{dt}{a}=\frac{1}{a}\displaystyle\int_\mathbb{R}(t-c)f(t)dt=$$

$$=\frac{1}{a}\Bigg[\displaystyle\int_\mathbb{R}tf(t)dt-c\displaystyle\int_\mathbb{R}f(t)dt\Bigg]=\frac{1}{a}(\mu-c)$$

$$\frac{\mu-c}{a}=0$$

$\mu-c=0$ zatem $c=\mu$

Zapisujemy

$$f_Z(x)=af(ax+\mu)$$

Stosujemy warunek na wariancję równą „1”

$$1=\displaystyle\int_\mathbb{R}x^2f_Z(x)dx-\Bigg(~~\underbrace{\displaystyle\int_\mathbb{R}xf_Z(x)dx}_{0}~~\Bigg)^2=\displaystyle\int_\mathbb{R}x^2af(ax+\mu)dx$$

$$=\begin{bmatrix}t=ax+\mu\\\frac{dt}{a}=dx\\x=\frac{t-\mu}{a}\end{bmatrix}=$$

$$=\displaystyle\int_\mathbb{R}\Bigg(\frac{t-\mu}{a}\Bigg)^2af(t)\frac{dt}{a}=\frac{1}{a^2}\displaystyle\int_\mathbb{R}\Big(t^2-2t\mu+\mu^2\Big)f(t)dt=$$

$$=\frac{1}{a^2}\Bigg[\displaystyle\int_\mathbb{R}t^2f(t)dt-2\mu\displaystyle\int_\mathbb{R}tf(t)dt+\mu^2\displaystyle\int_\mathbb{R}f(t)dt\Bigg]=…$$

ale

$$\sigma^2=\displaystyle\int_\mathbb{R}t^2f(t)dt-\Bigg(\displaystyle\int_\mathbb{R}tf(t)dt\Bigg)^2=\displaystyle\int_\mathbb{R}t^2f(t)dt-\mu^2$$

więc

$$\displaystyle\int_\mathbb{R}t^2f(t)dt=\sigma^2+\mu^2$$

$$…=\frac{1}{a^2}\Big(\sigma^2+\mu^2-2\mu^2+\mu^2\Big)=\frac{\sigma^2}{a^2}$$

$$\frac{\sigma^2}{a^2}=1$$

$$a^2=\sigma^2$$

$$a=\sigma$$

Funkcja gęstości jest funkcją dodatnią, dlatego odrzucamy $a=-\sigma$.

Ostatecznie

$$f_Z(x)=\sigma f(\sigma x+\mu)$$

Podsumowując, jeśli zmienna losowa $X$ pochodzi z rozkładu o wartości oczekiwanej $EX=\mu$ oraz skończonej wariancji $\text{Var}(X)=\sigma^{2}$, gdzie rozkład jest opisany funkcją gęstości $f(x)$, to standaryzowana zmienna losowa

$$Z=\frac{X-\mu}{\sigma}$$

pochodzi z rozkładu opisanego gęstością

$$f_Z(x)=\sigma f(\sigma x+\mu)$$

Standaryzacja dystrybuanty zmiennej losowej

Założenia

• $X$ – zmienna losowa z ciągłego rozkładu
• $\text{E}X=\mu$ – znane
• $\text{Var}(X)=\sigma^2$ – znane
• $f(x)$ – gęstość rozkładu – nie musi być znana
• $F(x)$ – dystrybuanta rozkładu – znana
• $f_Z(x)$ – standaryzowana gęstość – nie musi być znana

Standaryzowaną dystrybuantę wyznaczamy bezpośrednio

$$F_Z(x)=\displaystyle\int_{-\infty}^xf_Z(t)dt=\displaystyle\int_{-\infty}^x\sigma f\big(\sigma t+\mu\big)dt=$$

$$=\begin{bmatrix}u=\sigma t+\mu\\du=\sigma dt\\t=-\infty\Rightarrow u=-\infty\\t=x\Rightarrow u=\sigma x+\mu\end{bmatrix}=$$

$$=\displaystyle\int_{-\infty}^{\sigma x+\mu}f(u)du=F\big(\sigma x+\mu\big)$$

Ostatecznie

$$F_Z(x)=F\big(\sigma x+\mu\big)$$

Podsumowując, jeśli zmienna losowa $X$ pochodzi z rozkładu o wartości oczekiwanej $EX=\mu$ oraz skończonej wariancji $\text{Var}(X)=\sigma^{2}$, gdzie rozkład jest opisany dystrybuantą $F(x)$, to standaryzowana zmienna losowa

$$Z=\frac{X-\mu}{\sigma}$$

pochodzi z rozkładu opisanego dystrybuantą

$$F_Z(x)=F(\sigma x+\mu)$$

Standaryzacja odwrotnej dystrybuanty

Założenia

• $X$ – zmienna losowa z ciągłego rozkładu
• $\text{E}X=\mu$ – znane
• $\text{Var}(X)=\sigma^2$ – znane
• $F(x)$ – dystrybuanta rozkładu – nie musi być znana
• $F^{-1}(x)$ – odwrotna dystrybuanty rozkładu – znana
• $F_Z(x)$ – standaryzowana gęstość – nie musi być znana

Funkcja odwrotna do dystrybuanty, „pracując” na elemencie $y\in[0,1]$, zwraca wartość zmiennej losowej $X$, która odpowiada kwantylowi rzędu $y$ rozkładu $X$. Wartość funkcji jest więc wartością zmiennej losowej. Idąc tym tropem napiszemy, że standaryzowana odwrotna dystrybuanty przyjmuje wartość standaryzowanej zmiennej losowej

$$F_Z^{-1}(y)=\frac{X-\mu}{\sigma}=^{?}\frac{F^{-1}(x)-\mu}{\sigma}$$

Bardziej formalne uzasadnienie

$$y=F_Z(x)\Leftrightarrow x=F_Z^{-1}(y)$$

$$y=F_Z(x)=F(\sigma x+\mu)\Leftrightarrow \sigma x+\mu=F^{-1}(y)$$

Zapisując układ równań

$$\begin{cases}x=F_Z^{-1}(y)\\\sigma x+\mu=F^{-1}(y)\end{cases}$$

z drugiego równania mamy

$$x=\frac{F^{-1}(y)-\mu}{\sigma}$$

i na bazie pierwszego otrzymujemy

$$F_Z^{-1}(y)=x=\frac{F^{-1}(y)-\mu}{\sigma}$$

Podsumowując, jeśli zmienna losowa $X$ pochodzi z rozkładu o wartości oczekiwanej $EX=\mu$ oraz skończonej wariancji $\text{Var}(X)=\sigma^{2}$, gdzie rozkład jest opisany odwrotną dystrybuanty $F^{-1}(y)$, to standaryzowana zmienna losowa

$$Z=\frac{X-\mu}{\sigma}$$

pochodzi z rozkładu opisanego odwrotną dystrybuantą

$$F_Z^{-1}(y)=\frac{F^{-1}(y)-\mu}{\sigma}$$

Jedno zbiorcze twierdzenie na koniec

Jeśli zmienna losowa $X$ pochodzi z rozkładu o własnościach

• $EX=\mu$
• $\text{Var}(X)=\sigma^2$
• $f(x)$ – funkcja gęstości rozkładu
• $F(x)$ – dystrybuanta rozkładu
• $F^{-1}(y)$ – odwrotna dystrybuanty rozkładu

to standaryzowana zmienna losowa

$$Z=\frac{X-\mu}{\sigma}$$

pochodzi z rozkładu prawdopodobieństwa o własnościówkach

• $EX=0$
• $\text{Var}(X)=1$
• $f_Z(x)=\sigma f(\sigma x+\mu)$ – funkcja gęstości rozkładu
• $F_Z(x)=F(\sigma x+\mu)$ – dystrybuanta rozkładu
• $F_Z^{-1}(y)=\frac{F^{-1}(y)-\mu}{\sigma}$ – odwrotna dystrybuanty

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

https://youtu.be/YSOZPiXw6CY

https://youtu.be/XTOjmucEAsw

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa