„Co to jest różniczka? – zapytano matematyka.
Różniczka to wyniczek odejmowanka – odpowiedział”
🙂
Wzór Taylora to jeden z elementów, które stanowią esencję rachunku różniczkowego i całkowego. Oto, w magiczny sposób, na bazie sekwencji informacji o funkcji, dotyczących tylko jednego jej wybranego punktu, możliwe jest bardzo precyzyjne odtworzenie zmienności funkcji w pobliżu ustalonego punktu. Wzór Taylora, nazywamy często rozwinięciem Taylora funkcji $f(x)$ w otoczeniu punktu $x_0$, faktycznie „rozwija” funkcję do postaci sumy funkcji elementarnych $a_n(x-x_0)^n$, stanowiących atomy wielomianów. W efekcie otrzymujemy nie tylko efektywną aproksymację wartości funkcji, ale również nową „łatwiejszą” jej formę.
Wielomian Taylora
Twierdzenie Taylora: Dla funkcji $f:\mathbb{R}\to\mathbb{R}$ $n$-razy różniczkowalnej $(n\geq 1)$ w punkcie $x_0\in\mathbb{R}$, istnieje funkcja $h_n:\mathbb{R}\to\mathbb{R}$, że
$$f(x)=\underbrace{\displaystyle\sum_{k=0}^n\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k}_{wielomian-aproksymacja~f(x)}+\underbrace{h_n(x)(x-x_0)^n}_{reszta}$$
$$f(x)=f(x_0)+\frac{f^{(1)}(x_0)}{1!}(x-x_0)^1+\frac{f^{(2)}(x_0)}{2!}(x-x_0)^2+\ldots$$
$$\ldots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+h_n(x)(x-x_0)^n$$
oraz
$$\displaystyle\lim_{x\to x_0}h_n(x)=0$$
Przez $f^{(k)}(x)$ oznaczamy pochodną rzędu $k$ funkcji $f(x)$.
Twierdzenie Taylora nosi nazwę od angielskiego matematyka Brooka Taylora, który opracował je w 1712 roku. Samą własność wcześniej odkrył James Gregory – dokonał tego w 1671 roku.
Wzór, choć początkowo wygląda na dosyć skomplikowany, po bliższej analizie ujawnia niezwykłe piękno. Kolejne pochodne danej funkcji, wyznaczone w tym samym punkcie, kodują coraz „większą” i bardziej dokładną informację o kształcie funkcji w „szerszym” przedziale. Często sekwencja kilku / kilkunastu liczb wystarcza do osiągnięcia świetnej jakości aproksymacji. Jest to więc coś w rodzaju standaryzacji zapisu funkcji i algorytmu ich kompresji w jednym. Ten fenomen to główny przekaz artykułu – fenomen, który zostanie wyjaśniony w dalszej części tekstu.
Na bazie wzoru Taylora wprowadza się wielomian Taylora rzędu $n$ funkcji $f$.
$$T_n(x)=\displaystyle\sum_{k=0}^n\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k$$
Zalety wzoru Taylora – wybrane
- Wzór Taylora definiuje wielomian Taylora, który tym lepiej (zwykle) aproksymuje funkcję im wyższy jest jego stopień.
- Twierdzenie Taylora (w wersji powyższej z resztą w postaci Peano), daje informację o błędzie aproksymacji (notacja „o-małe” w zagadnieniach asymptotycznego tempa wzrostu). Istnieją inne dodatkowe nierówności pozwalające szacować resztę – po szczegóły kliknij tutaj.
- Wielomiany to funkcje elementarne, które bardzo łatwo wyznaczać numerycznie – z tego względu szereg kalkulatorów (czy programów / języków programowania) implementuje funkcje takie jak $\sin x$, $\cos x$, $e^x$, $\ldots$ poprzez odpowiednie wielomiany Taylora.
- Wielomiany z łatwością poddają się różniczkowaniu i całkowaniu.
- Wielomiany można zapisać w postaci iloczynowej, ułatwiając rozwiązywanie szeregu równań i nierówności.
- Wielomiany są określone na całej prostej rzeczywistej (lub płaszczyźnie zespolonej), co umożliwia analityczne „przedłużanie” wartości funkcji na dziedzinę, w której wyjściowa funkcja jest nieokreślona.
Przykład aproksymacji $e^x$ wielomianem Taylora – animacja
Animacja prezentuje rozwinięcie Taylora funkcji $e^x$ w otoczeniu punktu $x = 0$.
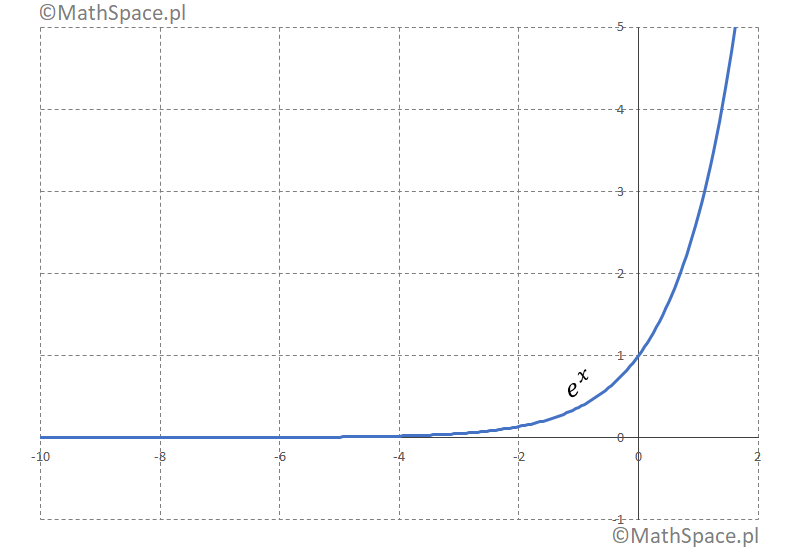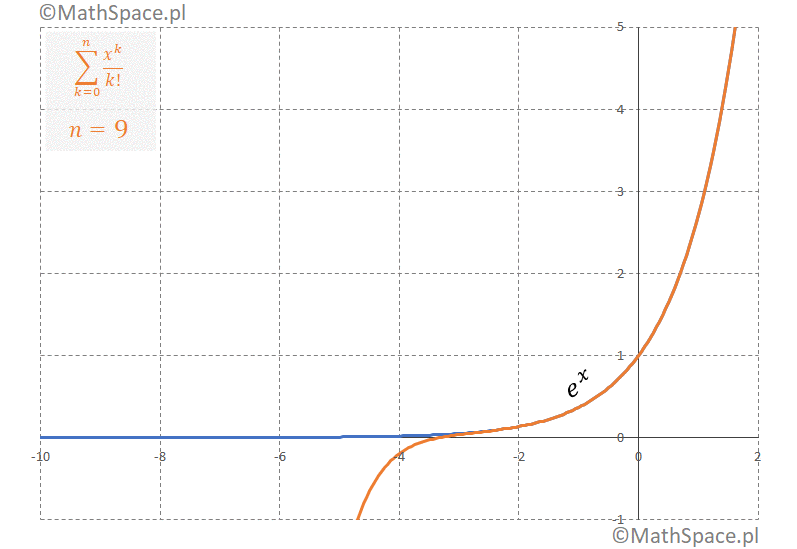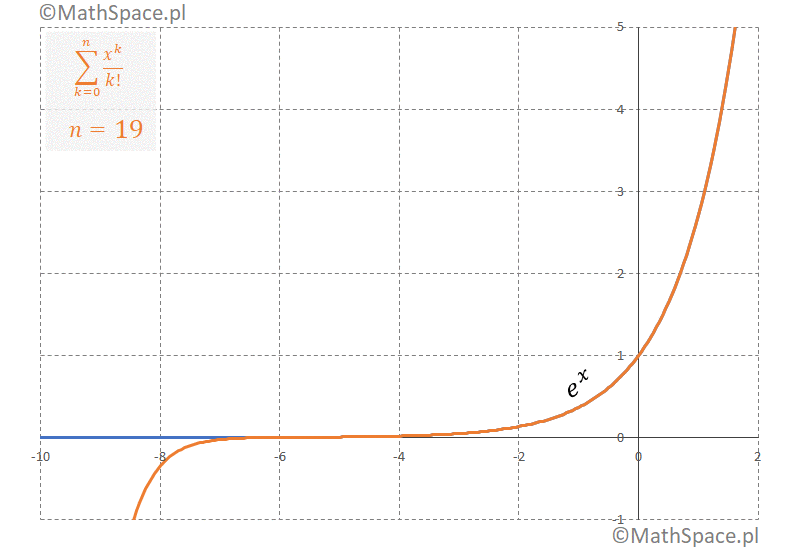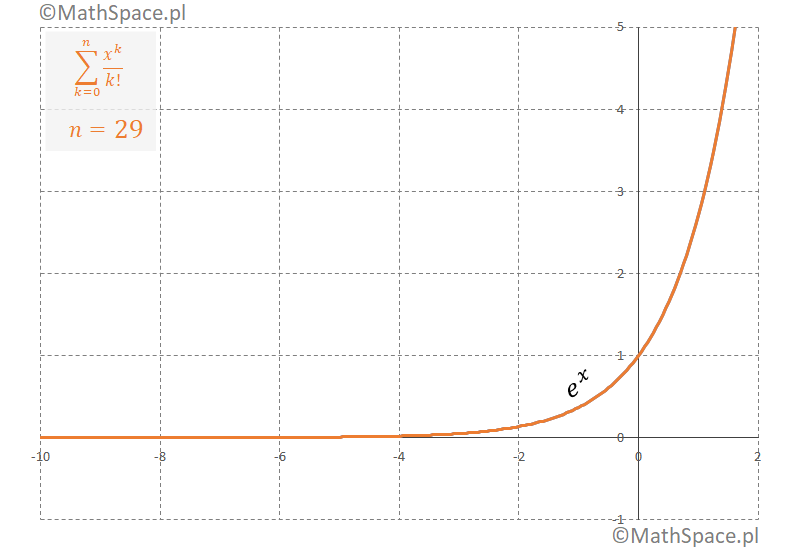
Dlaczego to działa?
Różniczka vs pochodna
Dział matematyki, badający własności funkcji na bazie pochodnych i całek, nazywamy rachunkiem różniczkowym i całkowym. Równania opisujące zależność pomiędzy funkcjami a ich pochodnymi nazywamy równaniami różniczkowymi. O funkcji, dla której możemy wyznaczyć pochodną, mówimy, że jest różniczkowalna. Nawet sam proces wyznaczania pochodnej nazywamy różniczkowaniem. Tymczasem różniczka ma w matematyce konkretne własne znaczenie.
Różniczka funkcji powstaje z jej pochodnej. Różniczka to funkcja dwóch niezależnych zmiennych. Można powiedzieć, że różniczka funkcji „to predykcja” przyrostu wartości funkcji (w zależności od przyrostu argumentu) na bazie informacji o pochodnej funkcji w danym punkcie.
Różniczka (definicja): jeśli funkcja $f:\mathbb{R}\to\mathbb{R}$ jest różniczkowalna w punkcie $x\in\mathbb{R}$, to jej różniczką nazywamy funkcję $df:\mathbb{R}\times\mathbb{R}\to\mathbb{R}$ określoną wzorem
$$df(x,\Delta x)=f^\prime(x)\cdot\Delta x$$
gdzie $x,\Delta x\in\mathbb{R}$
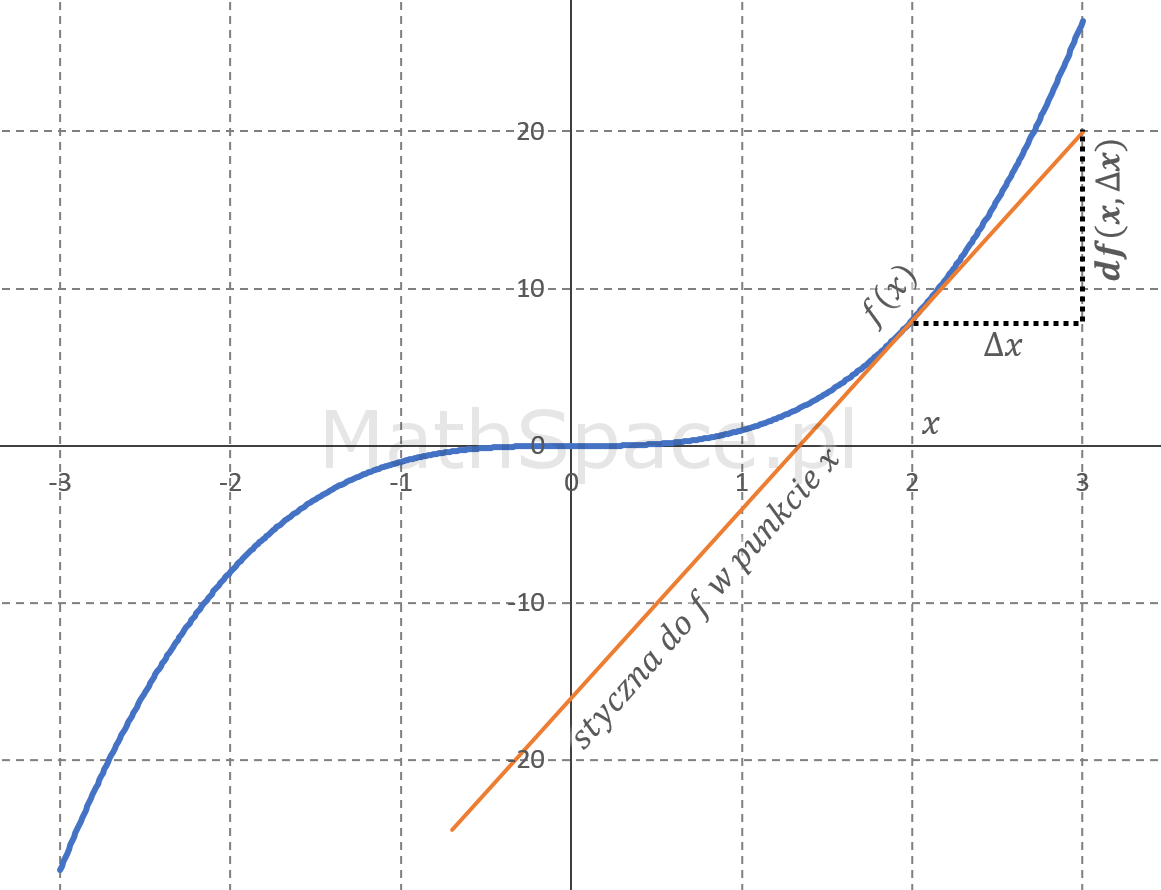
Ustalając pewien punkt $x_0\in\mathbb{R}$ możemy zapisać, że $\Delta x = x-x_0$, wtedy
$$df(x_0,\Delta x=x-x_0)=f^\prime(x_0)(x-x_0)$$
Łatwo zauważyć, że dodając do różniczki $df(x_0,\Delta x=x-x_0)$ wartość funkcji $f(x_0)$ otrzymujemy liniową aproksymację funkcji $f$ w pewnym otoczeniu punktu $x_0$
$$p(x)=f(x_0)+df(x_0,\Delta x=x-x_0)$$
$$p(x)=f(x_0)+f^\prime(x_0)(x-x_0)$$
gdzie
$$p(x_0)=f(x_0)$$
oraz
$$p^\prime(x_0)=f^\prime(x_0)$$
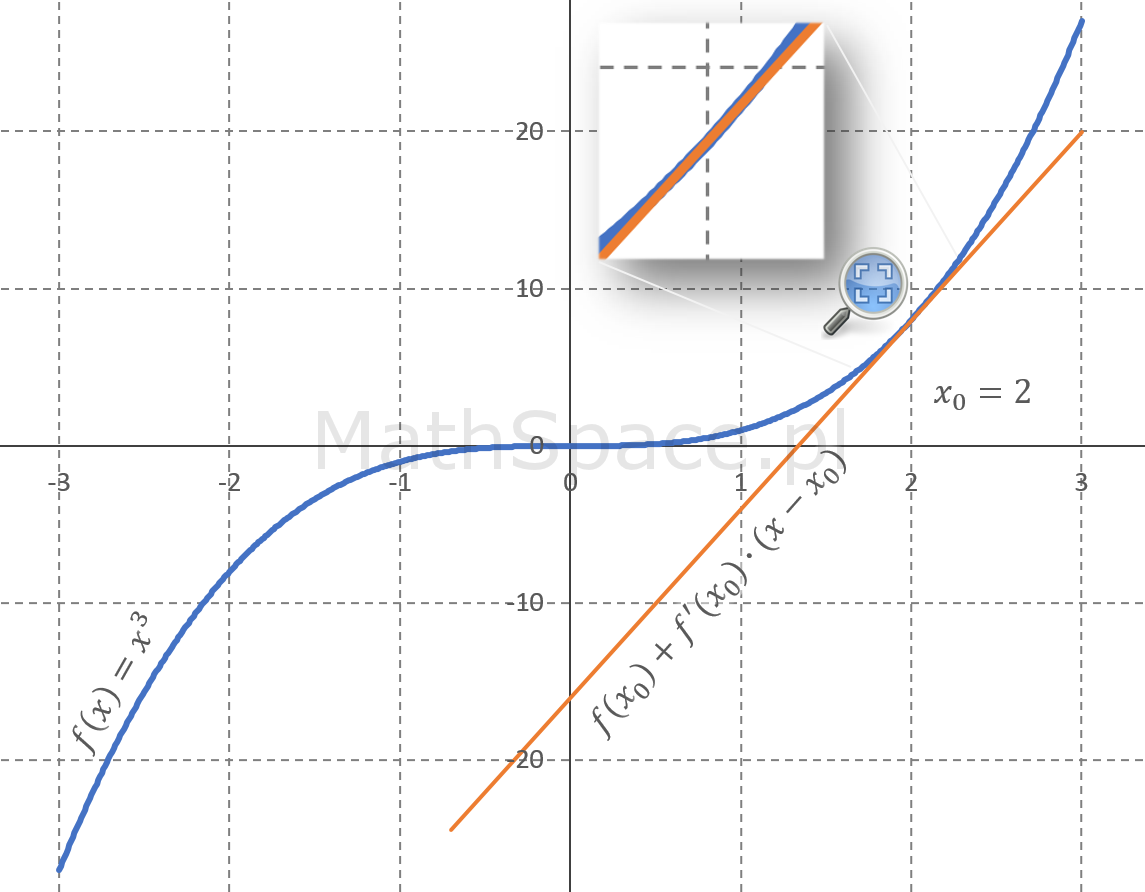
W pewnym sensie już widać, że we wzorze Taylora występują różniczki, wykorzystywane jako predykcje wzrostu wartości funkcji, wzrostu wartości pierwszej pochodnej, wzrostu wartości drugiej pochodnej, i tak dalej…
Kolejne pochodne kodują coraz więcej informacji o funkcji wyjściowej
Z definicji pochodna $f^\prime(x_0)$ mówi jak zmienia się funkcja $f(x)$ w otoczeniu $x_0$ (np. aproksymacja na bazie różniczki). Druga pochodna $f^{\prime\prime}(x_0)$ w punkcie $x_0$ wskazuje zmianę pierwszej pochodnej $f^\prime(x_0)$ w otoczeniu $x_0$. Do tej pory znaliśmy jedynie pierwszą pochodną w jednym punkcie, a na bazie informacji o drugiej pochodnej poszerzamy wiedzę o zachowaniu pierwszej pochodnej do pewnego przedziału. Tym samym rozszerza się przedział dobrej informacji na temat wyjściowej funkcji $f(x)$.
Znając $f(x_0)$ oraz wartości „punktowe” w $x_0$ kolejnych pochodnych $f^{(1)}(x_0)$, $f^{(2)}(x_0)$, $\ldots$, $f^{(n)}(x_0)$ wiedzę o zachowaniu funkcji $f(x)$ do coraz szerszych otoczeń punktu $x_0$ powiększamy stosując logikę:
- pochodna $f^{(n)}(x_0)$ rzędu $n$ w punkcie $x_0$ poszerza wiedzę o pochodnej $f^{(n-1)}(x)$ rzędu $n-1$ do otoczenia punktu $x_0$;
- tym samym wiedzę o $f^{(n-2)}(x)$ poszerzamy do jeszcze większego otoczenia $x_0$;
- i tak dalej, aż do pierwszej pochodnej, kończąc na zakodowanej informacji o funkcji wyjściowej.
Wielomian Taylora aproksymuje wartość funkcji poprzez aproksymowanie wartości jej kolejnych pochodnych.
Wspomniałem o tym już wcześniej, że gołym okiem we wzorze Taylora widać różniczki. Wszystko staje się znacznie jaśniejsze po wyznaczeniu kolejnych pochodnych wielomianu. Analizując poniższy schemat zwróć szczególną uwagę „jak wzór zwija się w lewo”.

Podstawiając $x_0$ do wzorów na pochodne wielomianu Taylora otrzymujemy oczywisty wniosek, że szacowane pochodne w punkcie $x_0$ będą zgodne z wyjściowymi wartościami pochodnych w punkcie $x_0$, co zapisujemy
$$T_n^{(k)}(x_0)=f^{(k)}(x_0)$$
$$k=0,1,\ldots,n$$
Wielomian Maclaurina
Wzór Maclaurina to szczególny przypadek wielomianu Taylora dla $x_0=0$ – reprezentuje więc rozwinięcie funkcji w otoczeniu punktu $x_0=0$.
$$T_n(x)=\displaystyle\sum_{k=0}^n\frac{f^{(k)}(0)}{k!}x^k$$
Rozwinięcie $e^x$ w wielomian Maclaurina
$f(x)=e^x$, $\quad$ $f^{(k)}(x)=e^x$
$x_0=0$, $\quad$ $f^{(k)}(0)=e^0=1$
$$T_n(x)=\displaystyle\sum_{k=0}^n\frac{x^k}{k!}=1+x+\frac{x^2}{2!}+\ldots+\frac{x^n}{n!}$$
Reprezentacja $e^x$: 1, 1, 1, 1, 1, 1, 1, 1, …

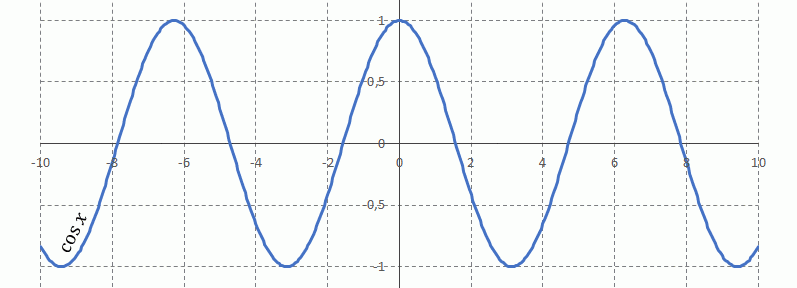
Rozwinięcie $\cos x$ w wielomian Maclaurina
$f(x)=\cos x$, $\quad$ $f(0)=1$
$f^\prime(x)=-\sin x$, $\quad$$ $f^\prime(0)=0$
$f^{\prime\prime}(x)=-\cos x$, $\quad$ $f^{\prime\prime}(0)=-1$
$f^{(3)}(x)=\sin x$, $\quad$ $f^{(3)}(0)=0$
$f^{(4)}(x)=\cos x$, $\quad$ $f^{(4)}(0)=1$
$$\cdots$$
Reprezentacja $\cos x$: 1, 0, -1, 0, 1, 0, -1, 0, …
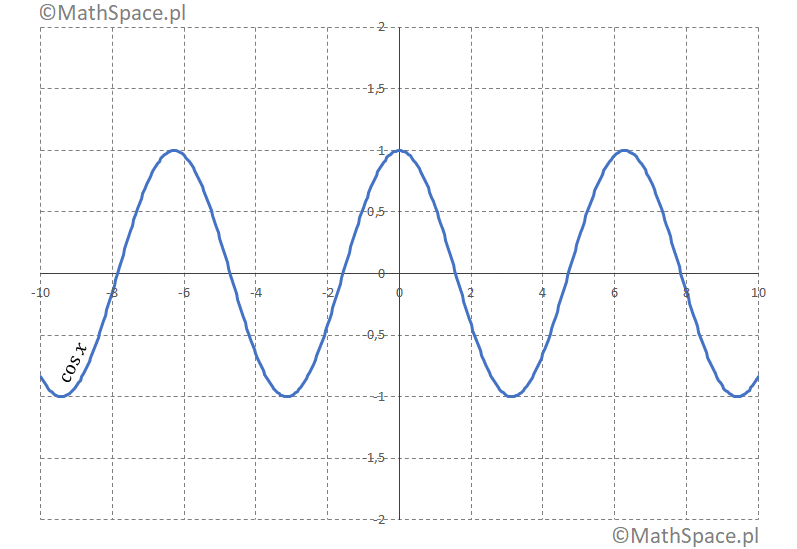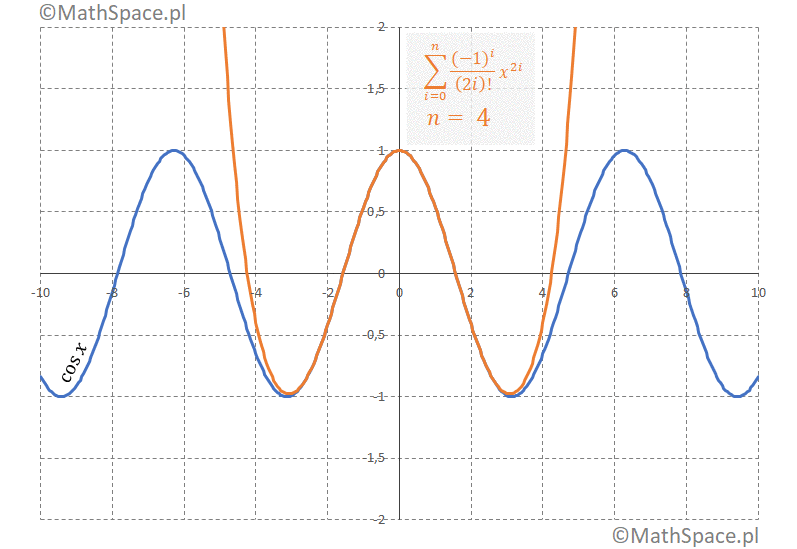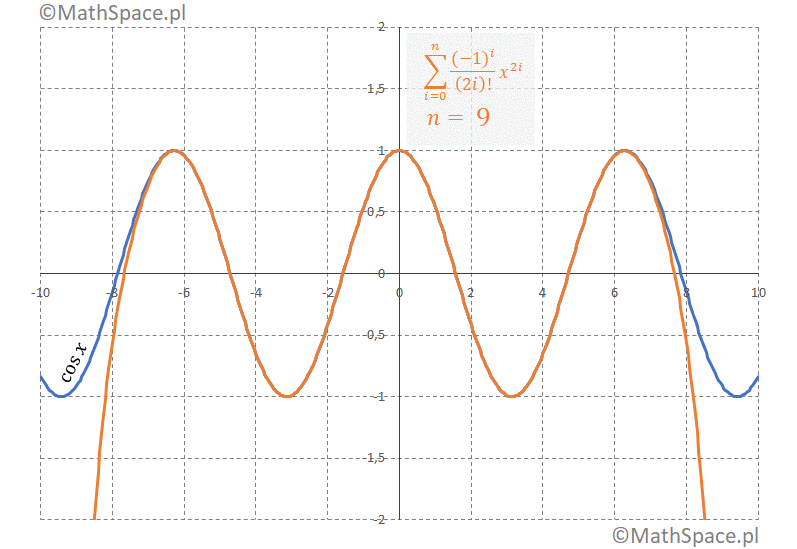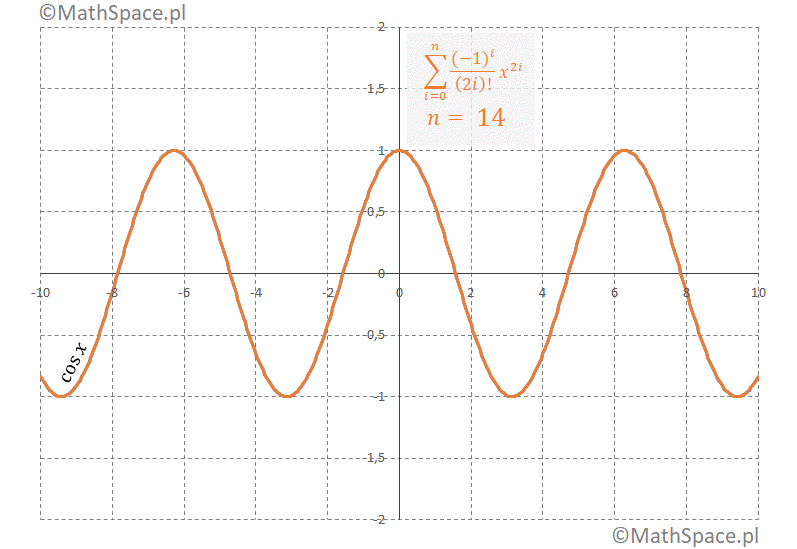
Szereg Taylora i Szereg Maclaurina
Dla funkcji nieskończenie wiele razy różniczkowalnych uzasadnione jest rozważanie nieskończonych wielomianów Taylora. Nieskończone sumy nazywamy szeregami, stąd
$$\displaystyle\sum_{n=0}^\infty\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n$$
nazywamy szeregiem Taylora, a
$$\displaystyle\sum_{n=0}^\infty\frac{f^{(n)}(0)}{n!}x^n$$
nazywamy szeregiem Maclaurina.
Tu w sposób naturalny pojawia się pytanie czy „nieskończony” wielomian Taylora jest zbieżny? Szereg Taylora jest szeregiem potęgowym, w związku z tym możliwe są trzy przypadki:
- szereg jest zbieżny dla wszystkich $x\in\mathbb{R}$;
- szereg jest zbieżny na pewnym odcinku $(x_0-r,x_0+r)$, poza tym odcinkiem szereg jest rozbieżny;
- szereg jest zbieżny tylko w jednym punkcie $x=x_0$.
Do badania zbieżności wykorzystuje się kryteria zbieżności dla szeregów potęgowych -po szczegóły kliknij tutaj.
Funkcja analityczna
Jeśli szereg Taylora (w otoczeniu dowolnego $x_0\in A$) funkcji $f:A\subseteq\mathbb{R}\to\mathbb{R}$ jest zbieżny i jego granicą jest właśnie funkcja $f$, to o $f$ mówimy, że jest analityczna na zbiorze $A$. Zachodzi wtedy zależność
$$f(x)=\displaystyle\sum_{n=0}^\infty\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n$$
Przykłady funkcji analitycznych w $\mathbb{R}$:
- $\sin x$
- $\cos x$
- $e^x$
Przykład funkcji, której szereg Taylora jest zbieżny, ale jego granica jest różna od wyjściowej funkcji
Twierdzenie: Funkcja $f:\mathbb{R}\to\mathbb{R}$
$$f(x)=\begin{cases}e^{-\frac{1}{x^2}}&\text{dla}\quad x\neq0\\0&\text{dla}\quad x=0\end{cases}$$
posiada rozwinięcie Taylora w otoczeniu $x_0=0$, które jest różne od $f(x)$ dla każdego $x\neq0$.
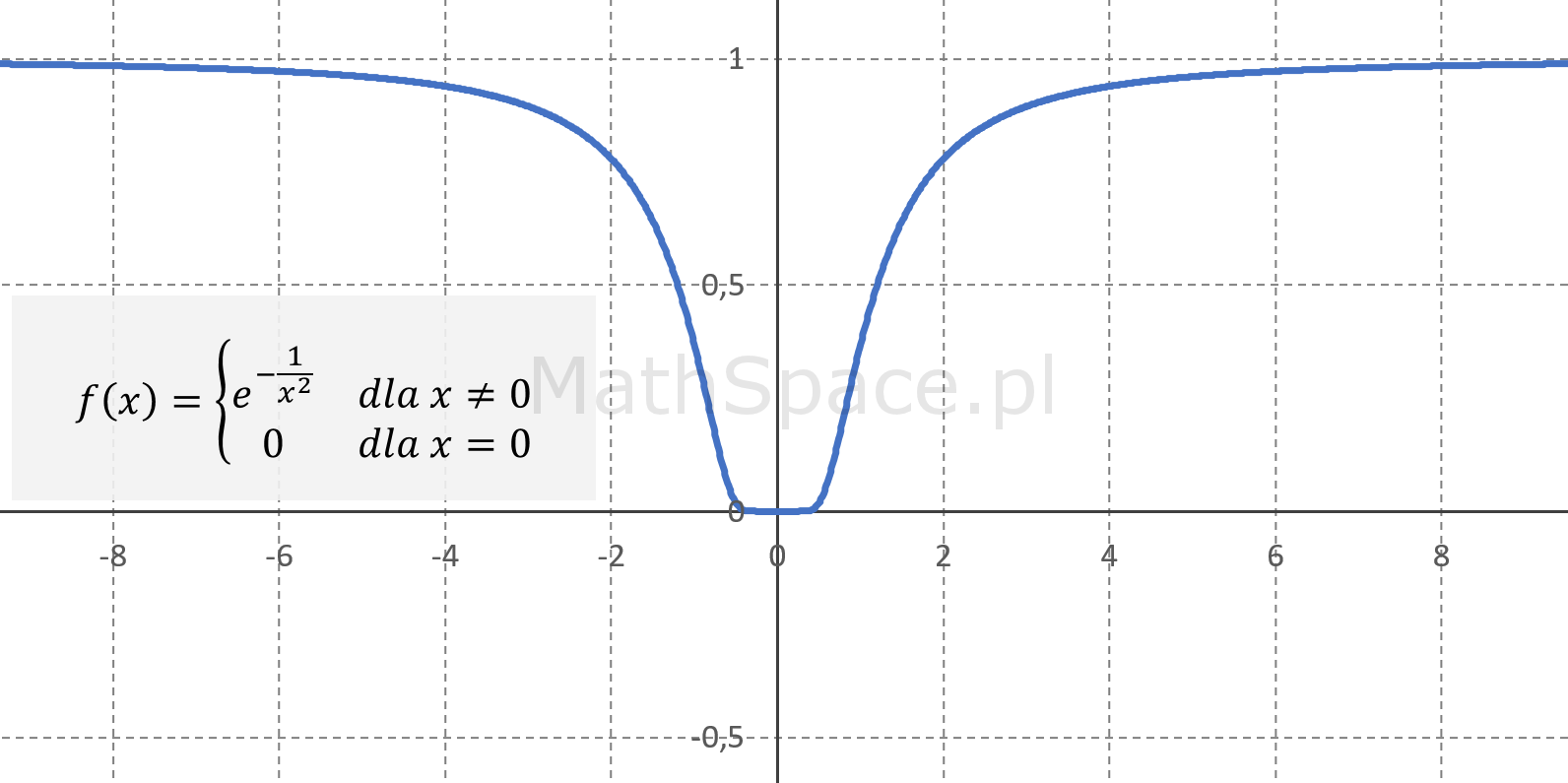
Funkcja $f$ jest nieskończenie wiele razy różniczkowalna w punkcie $x=0$, gdzie $f^{(n)}(0)=0$, więc jej szereg Taylora będzie funkcją stałą o wartości $0$, ale funkcja $f(x)\neq0$ dla $x\neq0$. Szczegóły znajdziesz w artykule „A Function which Does Not Equal its Taylor Series”.
Przedłużenie analityczne funkcji
Rozważmy funkcję $f:A\subset\mathbb{R}\to\mathbb{R}$ nieskończenie wiele razy różniczkowalną w punkcie $x_0$. Szereg Taylora funkcji $f$ jest przedłużeniem analitycznym funkcji $f$ na zbiór $B\supset A$ jeśli
- $\displaystyle\sum_{n=0}^\infty\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n=f(x)$ dla każdego $x\in A$ – tzn. szereg jest zbieżny do $f$ w jej dziedzinie;
- $\displaystyle\sum_{n=0}^\infty\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n=g(x)$ dla każdego $x\in B$ – tzn. szereg jest zbieżny do pewnej funkcji $g:B\subset\mathbb{R}\to\mathbb{R}$ na zbiorze $B$, którego podzbiorem jest $A$;
- $f(x)=g(x)$ dla każdego $x\in A$ – tzn. funkcje $f$ i $g$ są identyczne na dziedzinie funkcji $f$.
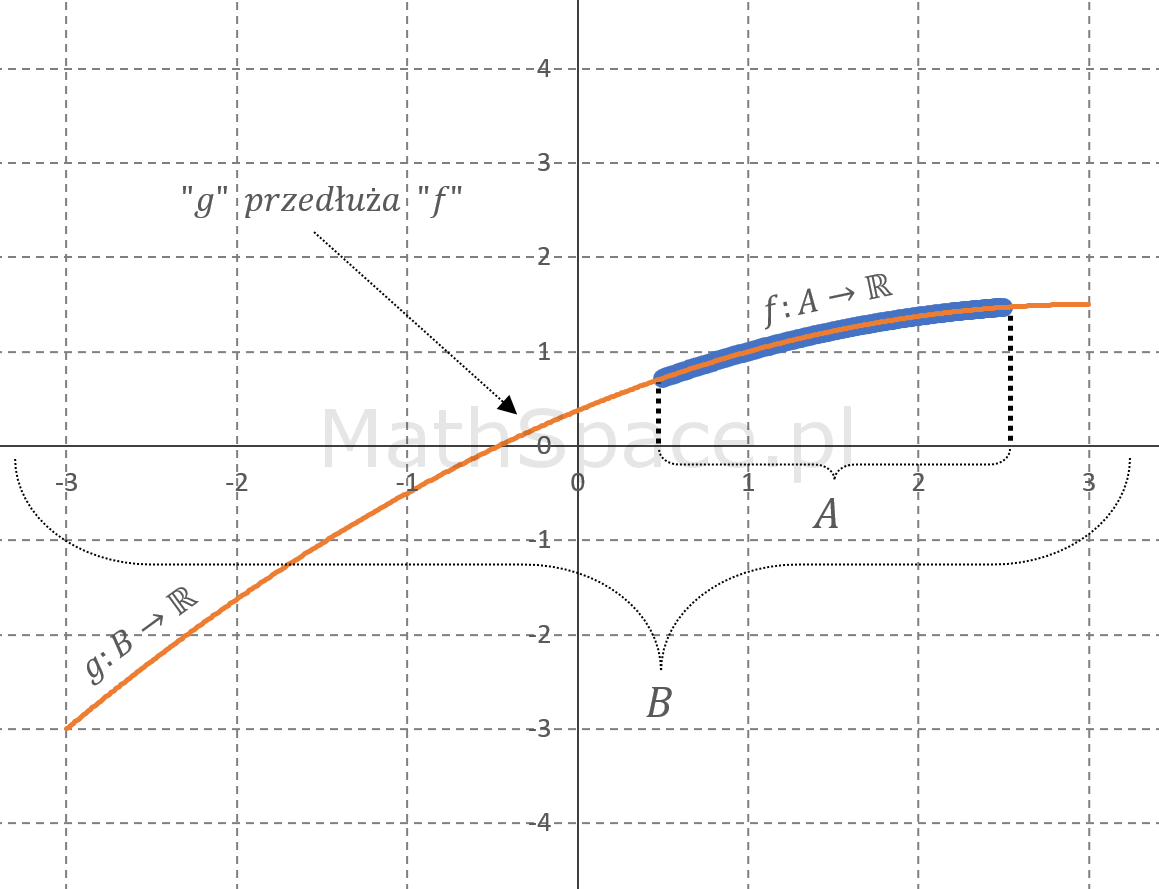
Analityczne przedłużanie funkcji stoi u podstaw analizy zespolonej, niesamowicie bogatej gałęzi matematyki.
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

Super!
Dziękuję 🙂
Genialny Blog, żałuje że nie znalazłem go wcześniej .
Dziękuję 🙂
Dzięki nie będę się nudził wieczorem
Dziękuję 🙂
Dziś się przydało
Super 🙂
Super artykuł 🙂
Dziękuję 🙂