Wszystkiego najlepszego w Dniu Liczby $\pi$ 🙂

Liczba $\pi$ ukryta w liczbach pierwszych? Jak to możliwe? Przecież liczby pierwsze to „chaos”, a $\pi$ ma ścisły związek z najbardziej regularnym obiektem geometrycznym – tzn. z okręgiem / kołem.

$P=\pi r^2$ to chyba najbardziej znany wzór, będący zarazem rzadko rozumianym 🙂 Choć wzór na pole powierzchni koła, bo o nim tu mowa, znany był już w Starożytnej Grecji, to jego uzasadnienie wcale nie jest łatwe. Jest to zatem świetny temat do wzbogacenia cyklu „Dlaczego?” 🙂 Do dzieła! 🙂

$$P=\pi r^2$$
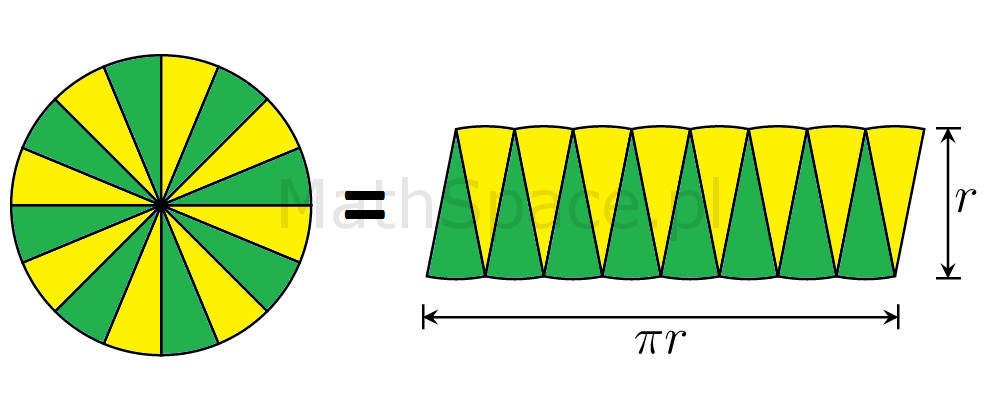
Jak widać powyżej – kwadrat i koło, o tej samej powierzchni, nie są „jakoś intuicyjnie łatwo” powiązane. Więcej – wykazano nawet, że kwadratura koła (procedura wykonywana przy użyciu cyrkla i linijki bez podziałki) jest niewykonalna! I tu pojawia się genialny pomysł z prostokątem 🙂 Nim powiem o co chodzi przyjrzyjmy się co tak naprawdę mówi wzór $$\pi r^2$$.
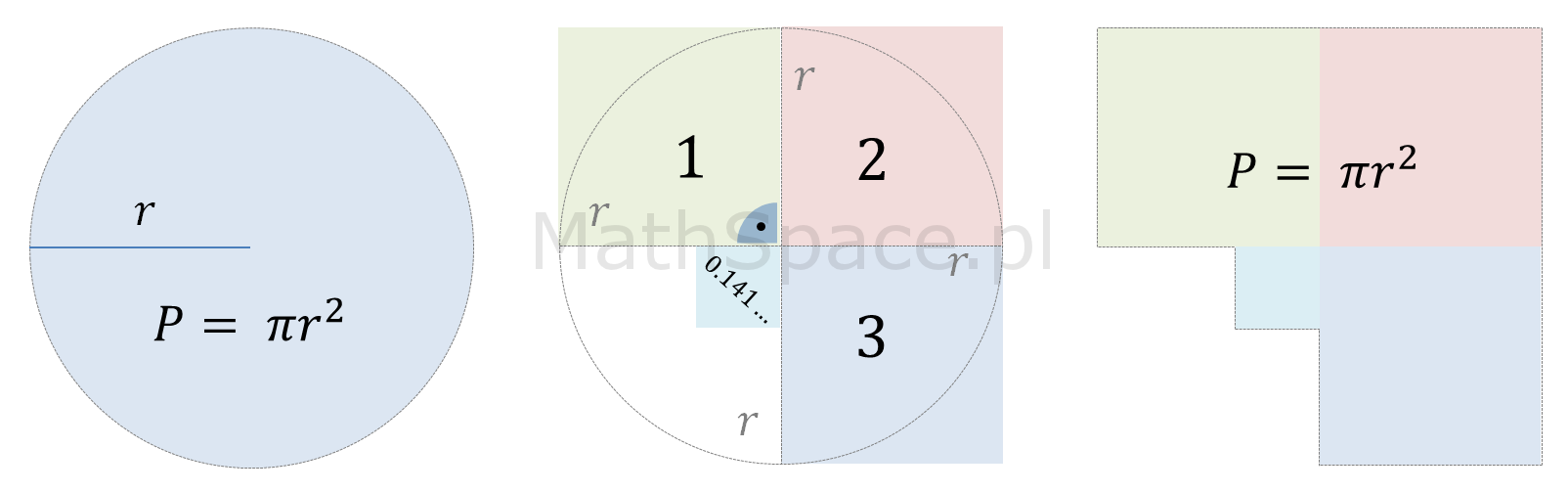
$\pi\times r^2$ – czyli w kole mieszczą się nieco ponad 3 kwadraty o boku r 🙂
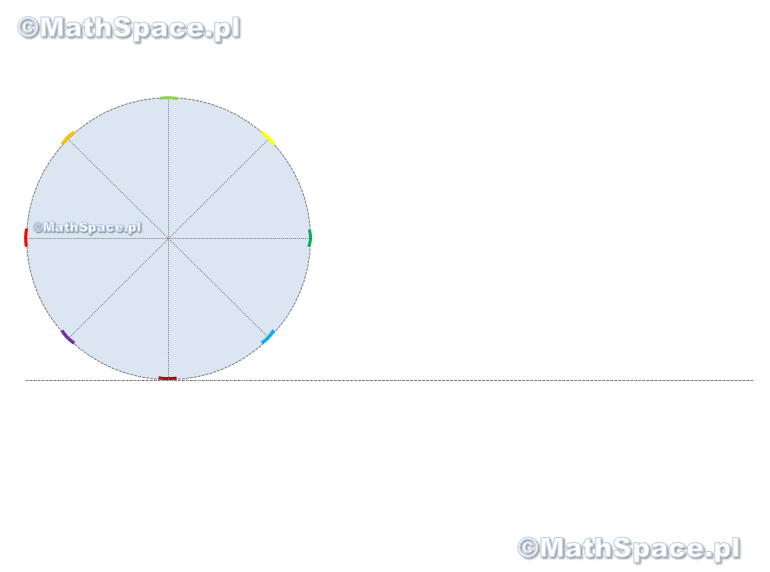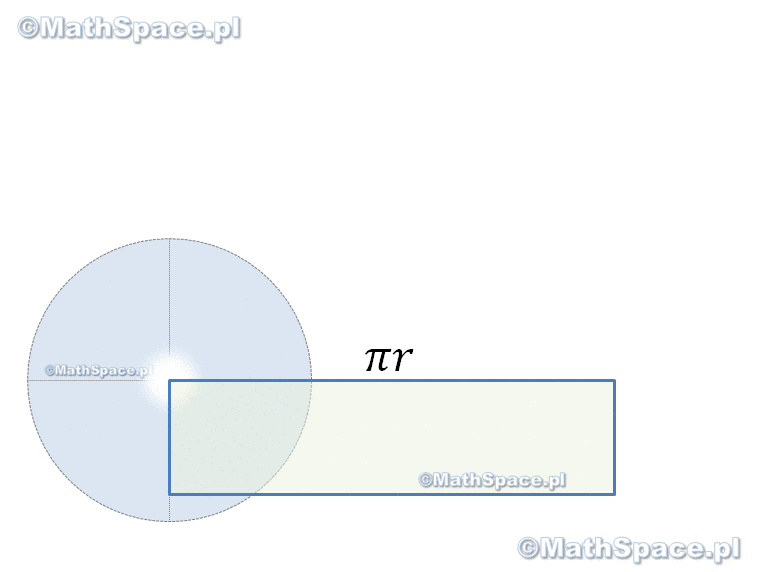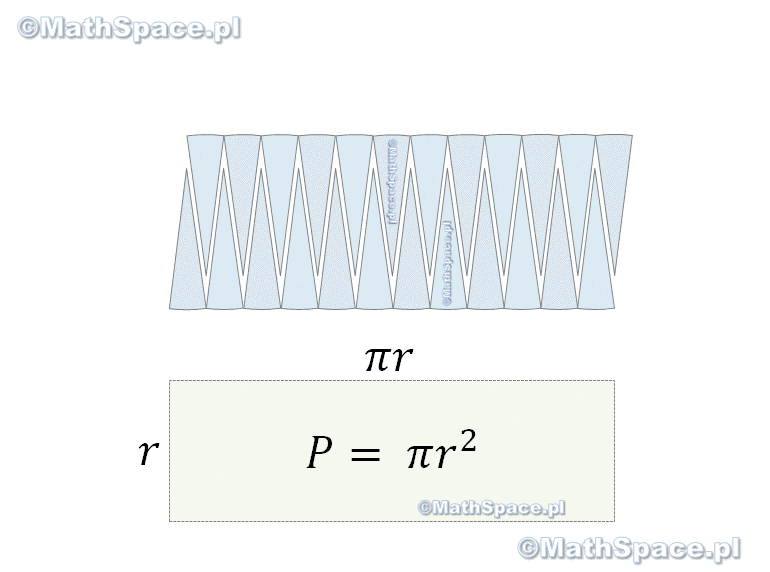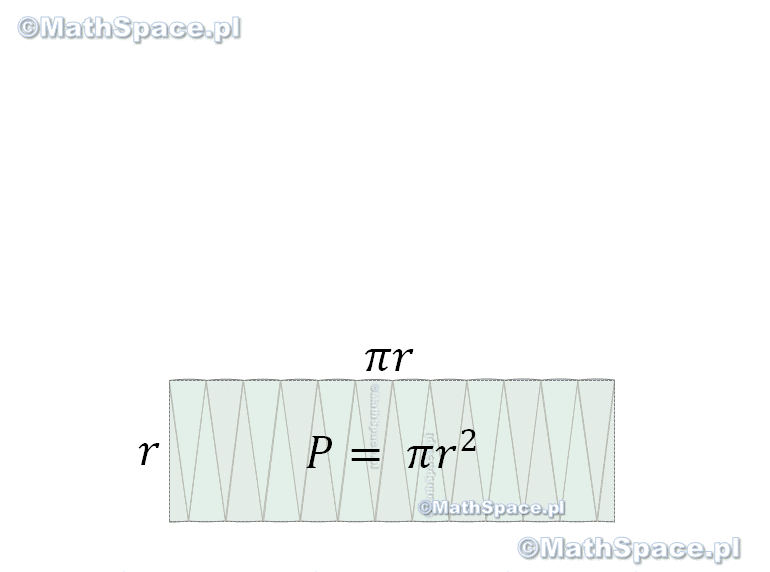
Trochę się napracowałem przy tej animacji 🙂
Uwaga – poniższe nie jest dowodem, a obrazuje jedynie sposób wnioskowania stosowany przez Starożytnych Greków (tak np. Archimedes wyznaczał liczbę pi).
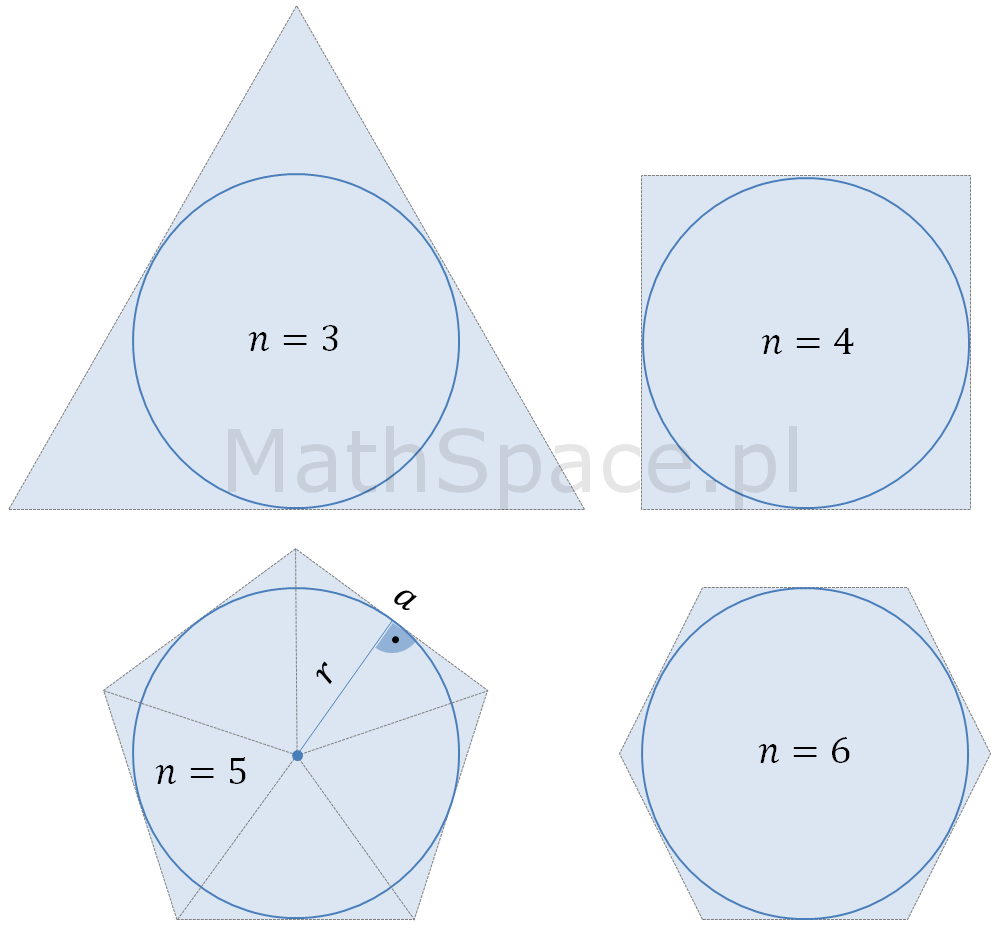
Można zauważyć, że obwód n-kąta foremnego opisanego na kole wynosi
$$O_n=na$$
a jego pole to suma pól trójkątów o podstawie $a$ i wysokości równej promieniowi koła $r$.
$$P_n=n\frac{ar}{2}=\frac{nar}{2}$$
Podstawiając
$$P_n=\frac{O_nr}{2}$$
Gdy n jest coraz większe, $P_n$ coraz dokładniej przybliża pole koła, a $O_n$ jego obwód. W „kroku granicznym” (zagadnienie wielkości nieskończenie małej) otrzymujemy
$O_n\to 2\pi r$ – tu z definicji liczby $\pi$
$$P_n\to\frac{2\pi rr}{2}=\pi r^2$$
Dowód, który przeprowadzę, nie będzie oparty na całkowaniu równania okręgu. Wykorzystam ciągi i ich granice oraz twierdzenie o trzech ciągach.
Niech będą dane trzy ciągi rzeczywiste $a_n$, $b_n$ i $c_n$. Jeśli „prawie wszędzie” (tzn. pomijając co najwyżej skończenie wiele wyrazów) zachodzi zależność
$$a_n\leq b_n\leq c_n$$
oraz
$$\lim a_n = \lim c_n = g$$
to
$$\lim b_n = g$$
Twierdzenie o trzech ciągach – strona na Wikipedii.
Pamiętam jak w szkole średniej, na lekcjach fizyki, mój nauczyciel wielokrotnie przyjmował, że dla małych $x$ funkcję $\sin x$ dobrze przybliża właśnie $x$. Wynika to z rozwinięcia $\sin x$ w szereg Taylora – wyjaśnienie pomijam. Wyznaczę jednak samą granicę – bo się przyda 🙂
$$\lim_{x\to 0}\frac{\sin x}{x}=\big(\frac{0}{0}\big)\text{ reg. de l`Hospitala}=$$
$$=\lim_{x\to 0}\frac{(\sin x)\prime}{x\prime}=\lim_{x\to 0}\frac{\cos x}{1}=$$
$$=\frac{\cos 0}{1}=\frac{1}{1}=1$$
$$\lim_{x\to 0}\frac{\sin x}{x} = 1$$
Reguła de l’Hospitala – Wikipedia
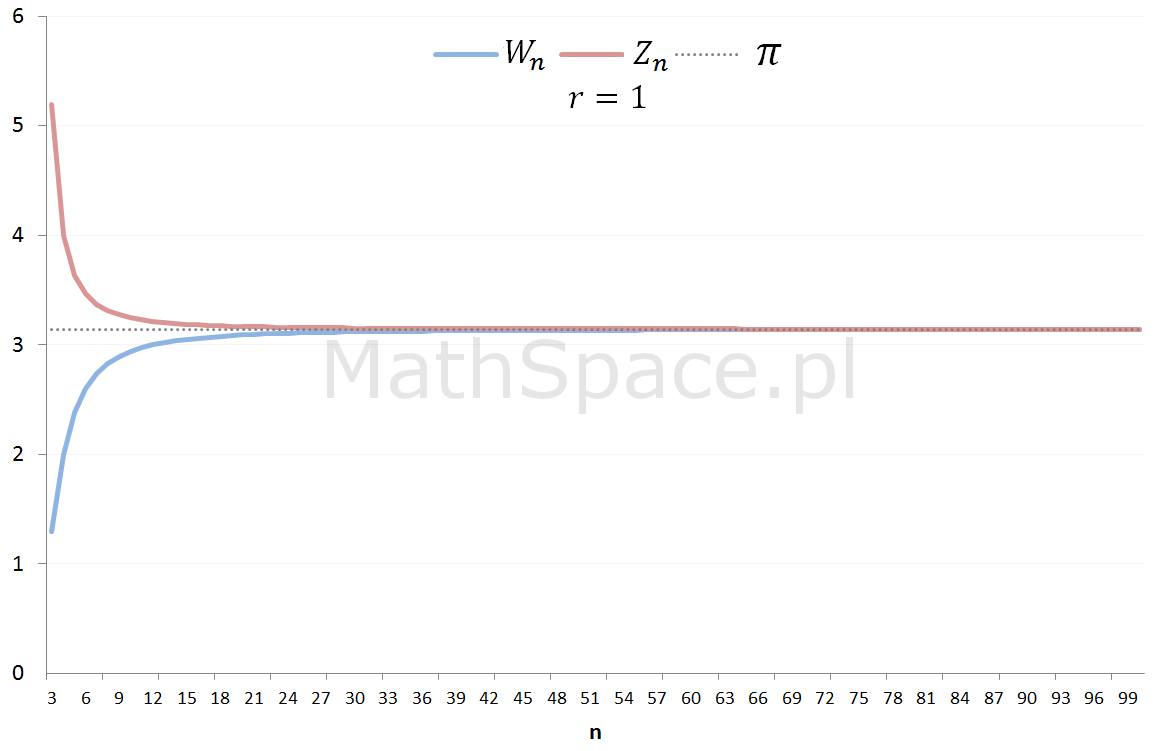
Rozważmy n-kąty foremne opisane na kole i wpisane w koło. Pole n-kąta opisanego nazwijmy „polem zewnętrznym” i oznaczmy $Z_n$. Analogicznie pole n-kąta wpisanego nazwiemy „polem wewnętrznym” oznaczając je $W_n$.
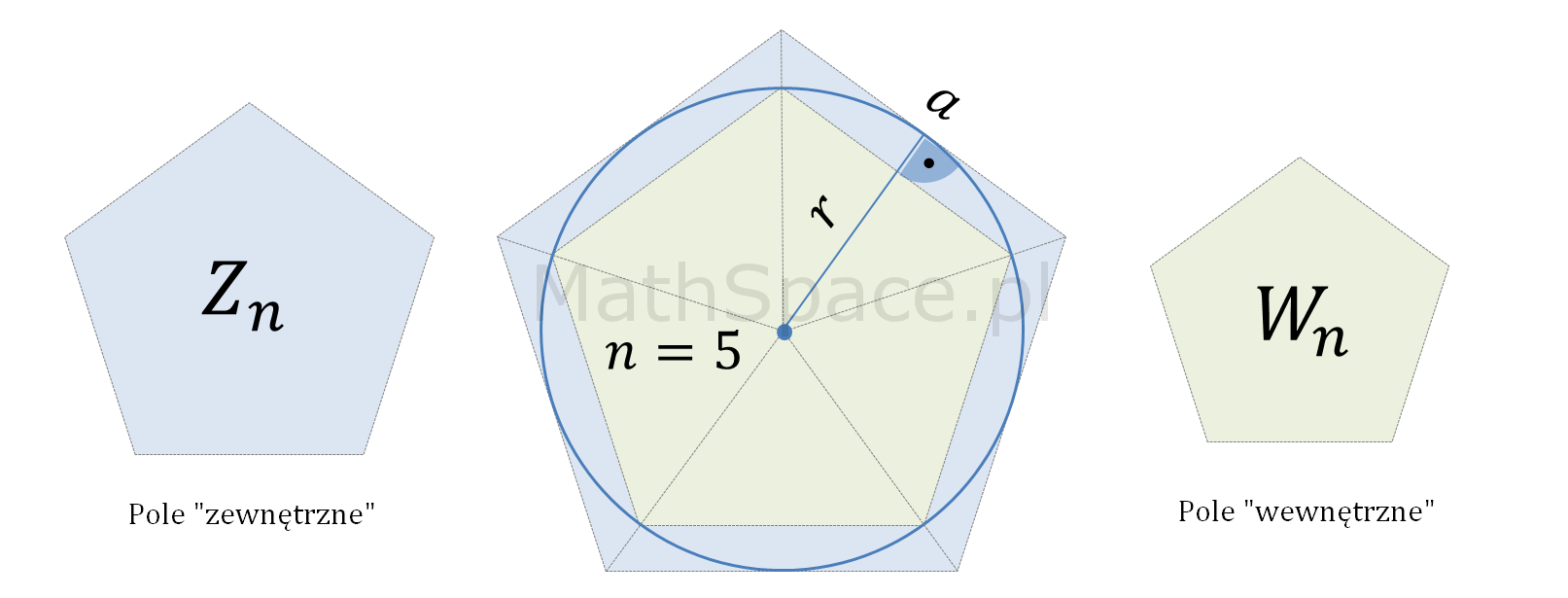
Oczywiście
$$W_n\leq P\leq Z_n$$
gdzie $P$ oznacza pole koła.
W kolejnym kroku dzielimy n-kąty na n-trójkątów. Zauważmy, że w ten sposób kąt pełny został również podzielony na n równych części. Pole „trójkąta zewnętrznego” oznaczymy przez $T_n$, a trójkąta wewnętrznego $t_n$.
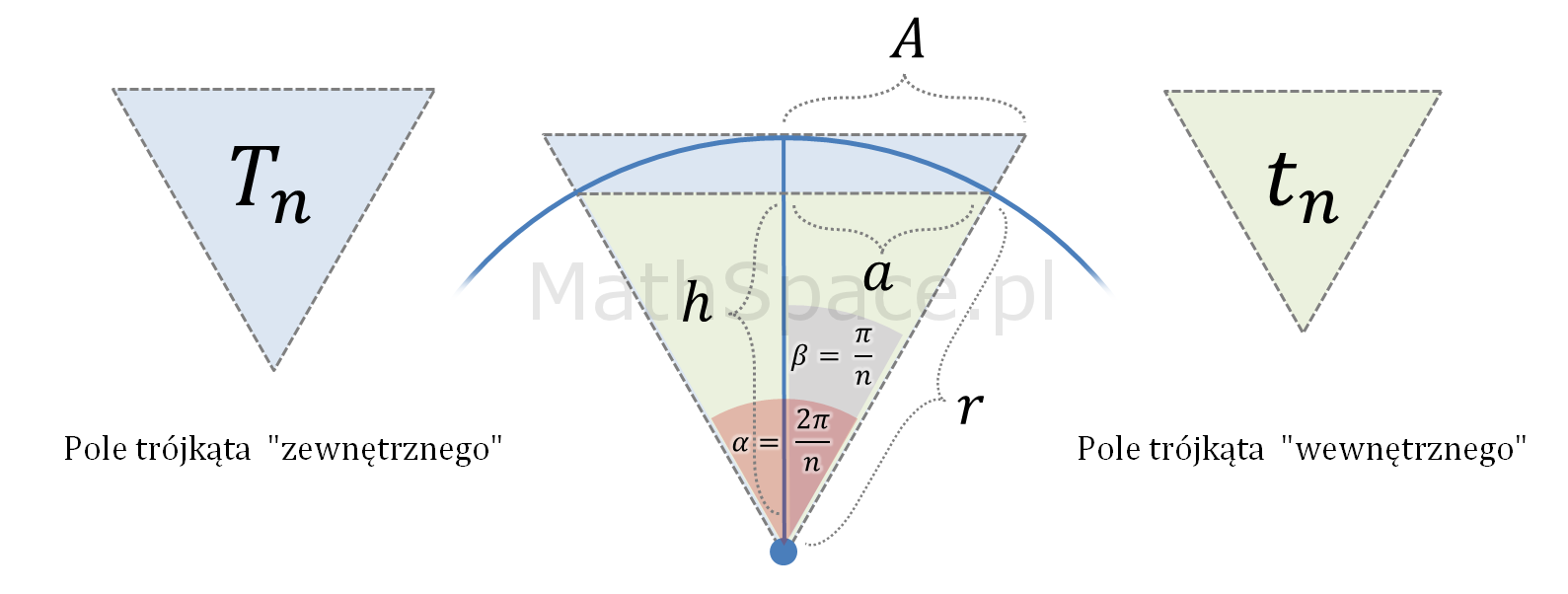
$$Z_n=nT_n$$
$$W_n=nt_n$$
$$T_n=Ar$$
ale
$$\frac{A}{r}=\text{tg}\beta=\frac{\sin\beta}{\cos\beta}$$
$$\frac{A}{r}r^2=r^2\frac{\sin\beta}{\cos\beta}$$
$$Ar=r^2\frac{\sin\beta}{\cos\beta}$$
$$T_n=r^2\frac{\sin\beta}{\cos\beta}=r^2\frac{\sin\frac{\pi}{n}}{\cos\frac{\pi}{n}}$$
$$t_n=ah$$
ale
$$\frac{a}{r}=\sin\beta$$
$$a=r\sin\beta$$
oraz
$$\frac{h}{r}=\cos\beta$$
$$h=r\cos\beta$$
podstawiając
$$t_n=r\sin\beta\cdot r\cos\beta=r^2\sin\beta\cos\beta$$
stosując tożsamości trygonometryczne
$$t_n=r^2\sin\beta\cos\beta=\frac{r^2}{2}2\sin\beta\cos\beta=$$
$$=\frac{r^2}{2}\sin2\beta=\frac{r^2}{2}\sin\alpha$$
$$t_n=\frac{r^2}{2}\sin\alpha=\frac{r^2}{2}\sin\frac{2\pi}{n}$$
$$Z_n=nT_n=nr^2\frac{\sin\frac{\pi}{n}}{\cos\frac{\pi}{n}}$$
$$W_n=nt_n=\frac{nr^2}{2}\sin\frac{2\pi}{n}$$
$$\lim Z_n=\lim nr^2\frac{\sin\frac{\pi}{n}}{\cos\frac{\pi}{n}}=$$
$$=\lim \frac{nr^2}{\cos\frac{\pi}{n}}\cdot\frac{\pi}{n}\cdot\frac{\sin\frac{\pi}{n}}{\frac{\pi}{n}}=$$
$$=\lim \frac{\pi r^2}{\cos\frac{\pi}{n}}\cdot\frac{\sin\frac{\pi}{n}}{\frac{\pi}{n}}=\frac{\pi r^2}{\cos 0}\cdot 1=$$
$$=\frac{\pi r^2}{1}=\pi r^2$$
$$\lim Z_n=\pi r^2$$
$$\lim W_n=\lim\frac{nr^2}{2}\sin\frac{2\pi}{n}=$$
$$\lim \frac{nr^2}{2}\cdot \frac{2\pi}{n}\cdot\frac{\sin\frac{2\pi}{n}}{\frac{2\pi}{n}}=$$
$$\lim \pi r^2\cdot\frac{\sin\frac{2\pi}{n}}{\frac{2\pi}{n}}=\pi r^2\cdot 1=\pi r^2$$
$$\lim W_n=\pi r^2$$
Z twierdzenia o trzech ciągach wnioskujemy, że pole koła to
$$P=\lim W_n=\lim Z_n=\pi r^2$$
🙂
Pozdrowienia,
Mariusz Gromada
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
Dziś ciekawostka w nawiązaniu do wpisu z dnia 20 października 2015 roku „Liczba PI ukryta w zbiorze Mandelbrota”, ujawniająca nietrywialne powiązanie liczby $\pi$ z prędkością ucieczki do nieskończoności przy zbliżaniu się punktu startu iteracji do „ostrza” zbioru Mandelbrota. Brzmi trochę skomplikowanie? Poniżej wyjaśnienie 🙂
Rozważmy równanie rekurencyjne dla liczb rzeczywistych
$$x_n=\begin{cases}x_{n-1}^2+\frac{1}{4}+\epsilon&\text{dla}\quad n>0\\0&\text{dla}\quad n=0\end{cases}$$
Powyższe wyrażenie powstaje na bazie równania (w liczbach zespolonych) opisującego zbiór Mandelbrota
$$z_n=z_{n-1}^2+c$$
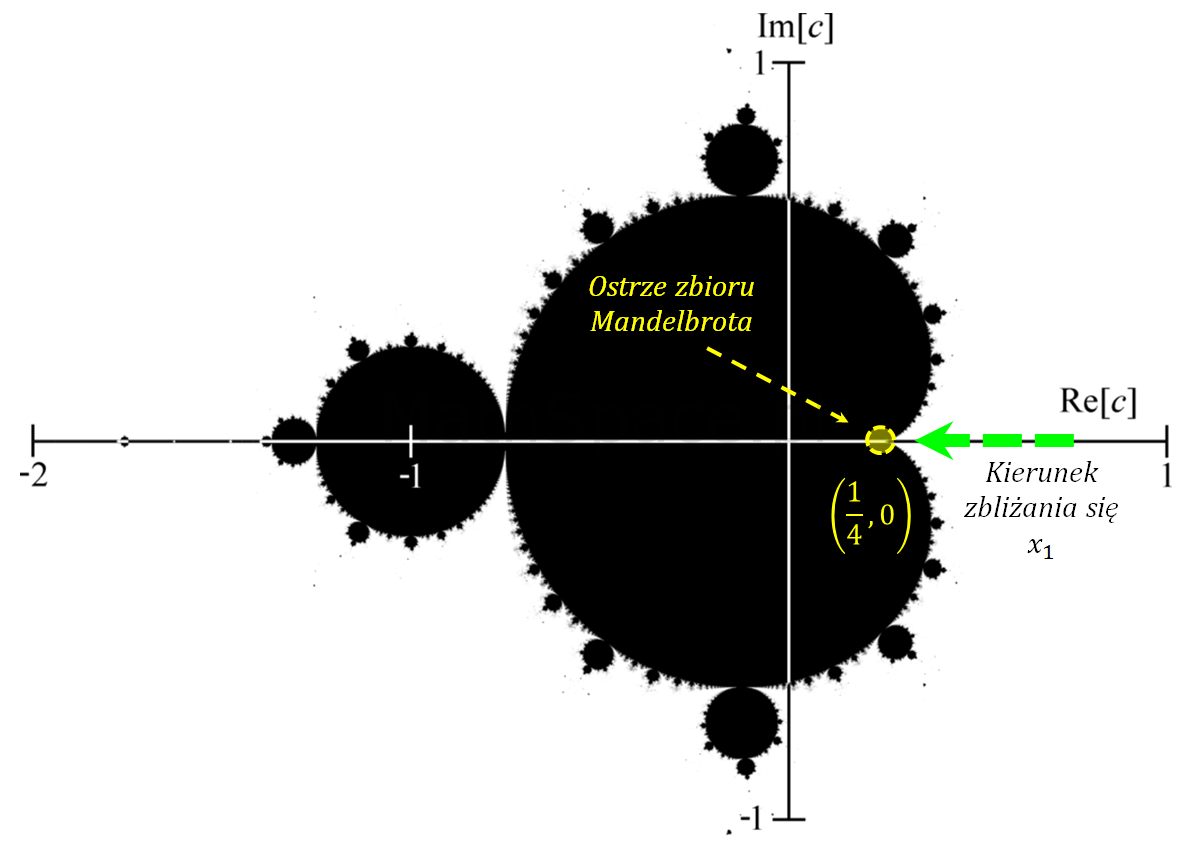
Ograniczając się do prostej rzeczywistej (dlatego użyłem zapisu $x_n$) przeanalizujmy zachowanie $x_n$ przy zbliżaniu się elementu $x_1=\frac{1}{4}+\epsilon$ do „ostrza” (ang. „cusp”) zbioru – ostrze to punkt o współrzędnych $(\frac{1}{4},0)$.
Ustalając odpowiednio małe $\epsilon>0$ decydujemy jak bardzo chcemy się zbliżyć do „ostrza”. Teraz zadanie polega na znalezieniu pierwszego $n$, dla którego $x_n>=2$. Takie minimalne $n$ jest dobrą miarą prędkości ucieczki $x_n$ do nieskończoności w zależności od wybranego $\epsilon$. Na marginesie dodam, że zbiór Juli dla równania Mandelbrota (na powyższym obrazku oznaczony kolorem czarnym), reprezentuje punkty „nieuciekające” do nieskończoności w trakcie nieskończonej iteracji . Ta tematyka jest sama w sobie bardzo ciekawa i zapewne kiedyś coś napiszę o atraktorach.
$$x_n=\begin{cases}x_{n-1}^2+\frac{1}{4}+\epsilon&\text{dla}\quad n>0\\0&\text{dla}\quad n=0\end{cases}$$
$$N_\epsilon=\min\big\{n~|~x_n\ge2\big\}$$
W celu poszukiwania rozwiązania zapisujemy zadanie wykorzystując rekurencję
$$N(n,\epsilon)=\begin{cases}N(n+1,\epsilon)&\text{dla}\quad x_n<2\\n&\text{dla}\quad x_n>=2\end{cases}$$
Nietrudno zauważyć, że zdefiniowaliśmy rekurencję na rekurencji. To zły znak dla wydajności.
/* Definicja funkcji rekurencyjnej */ Function x = new Function("x(n, eps) = if( n &amp;gt; 0, x(n-1, eps)^2 + 0.25 + eps, 0 )"); Function N = new Function("N(n, eps) = if( x(n, eps) &amp;gt;= 2, n, N(n+1, eps) )", x); /* Obliczenia i wyświetlenie wyniku */ mXparser.consolePrintln( "eps = 0.01" + ", N(0, eps) = " + N.calculate(0, 0.01) + ", czas = " + N.getComputingTime() + " s" ); mXparser.consolePrintln( "eps = 0.0001" + ", N(0, eps) = " + N.calculate(0, 0.0001) + ", czas = " + N.getComputingTime() + " s" ); mXparser.consolePrintln( "eps = 0.000001" + ", N(0, eps) = " + N.calculate(0, 0.000001) + ", czas = " + N.getComputingTime() + " s" ); mXparser.consolePrintln( "eps = 0.00000001" + ", N(0, eps) = " + N.calculate(0, 0.00000001) + ", czas = " + N.getComputingTime() + " s" );
+ wyczekiwany wynik
eps = 0.01, N(0, eps) = 30.0, czas = 0.224 s eps = 0.0001, N(0, eps) = 312.0, czas = 1.532 s eps = 0.000001, N(0, eps) = 3140.0, czas = 37.343 s eps = 0.00000001, N(0, eps) = 31414.0, czas = 4068.338 s
$$\epsilon=\frac{1}{10}\Rightarrow N_\epsilon=30$$
$$\epsilon=\frac{1}{1000}\Rightarrow N_\epsilon=312$$
$$\epsilon=\frac{1}{100000}\Rightarrow N_\epsilon=3140$$
$$\epsilon=\frac{1}{10000000}\Rightarrow N_\epsilon=31414$$
…
WOW! Jaki super wzorzec liczby wymaganych iteracji, aby przekroczyć 2! Dostajemy coś, co przypomina $\pi$, jednak wymaga postawienia „przecinka” w odpowiednim miejscu! Można również zauważyć, że 100-krotne zmniejszenie $\epsilon$ zwiększa niezbędną liczbę iteracji około 10-krotnie. Zmniejszając $\epsilon$ otrzymujemy liczbę coraz bardziej „przypominającą” $\pi$ 🙂

Pozdrowienia,
Mariusz Gromada
Zobacz również:
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
Alexander J. Yee i Shigeru Kondo w grudniu 2013 roku wyznaczyli liczbę Pi z dokładnością do ponad 12 bilionów cyfr – zdumiewająca precyzja! Dalszych obliczeń zaniechano w związku z wyczerpaniem się przestrzeni dyskowej. W poniższym tekście chciałbym przybliżyć co tak wielka dokładność może oznaczać w praktyce.
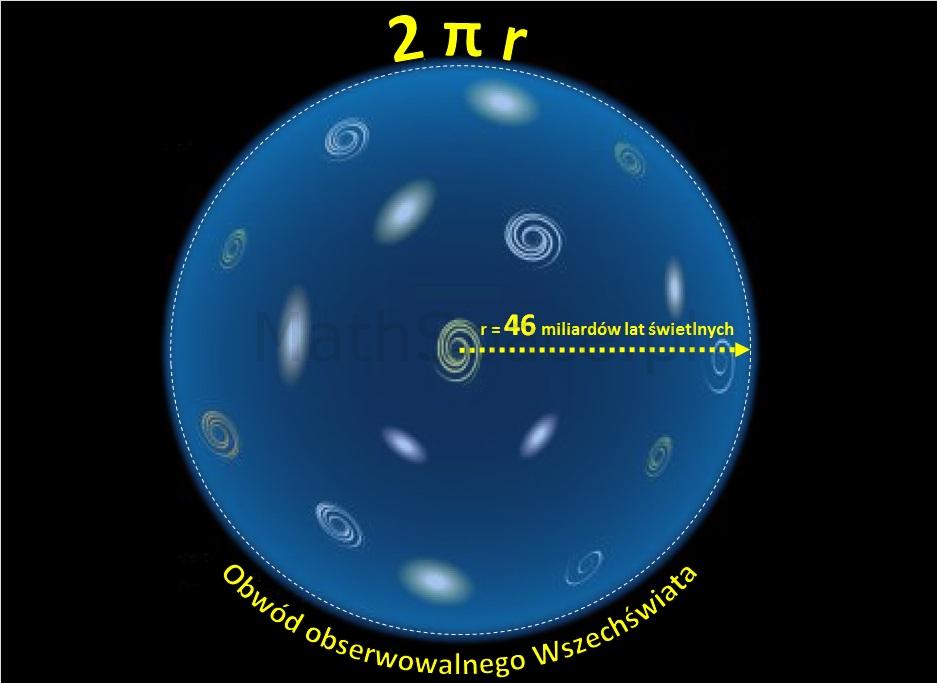
Rozważmy rozmiar Obserwowalnego Wszechświata zadając pytanie jakiej precyzji liczby Pi potrzeba do wyznaczenia jego obwodu z dokładnością rzędu 1 atomu wodoru? Promień walencyjny wodoru to 37 pm = 3.7×10 ‾¹¹ m. Rozmiar Obserwowalnego Wszechświata to suma odległości jaką światło przebyło od momentu Wielkiego Wybuchu (13.8 miliarda lat świetlnych) oraz dystansu, o jaki oddaliły się (przez ten okres) najodleglejsze galaktyki. Obecnie szacowana średnica Obserwowalnego Wszechświata to 92 miliardy lat świetlnych.
Promień rzędu 46 miliardów lat świetlnych zdaje się sugerować, że oddalanie się galaktyk musiało się odbywać z prędkością większą niż prędkość światła. „Oddalanie się galaktyk” to uproszczenie myślowe – faktyczne oddalanie się jest konsekwencją ekspansji Wszechświata, która to jest rozszerzaniem się przestrzeni. Wielki Wybuch jest momentem rozpoczęcia ekspansji, czyli początkiem rozszerzania się przestrzeni. Fotony, które teraz obserwujemy, „leciały” do nas 13.8 miliarda lat, ale w momencie kiedy „startowały” to punkt startu i punkt docelowy były znacznie bliżej siebie. Wraz z podróżą fotonu przestrzeń się rozszerzała sprawiając, że przebyta droga była dłuższa, jak i dłuższa (niż początkowo) jest droga jeszcze „do przebycia”. Niezgodność z zasadą niemożliwości przekroczenia prędkości światła jest w tym przypadku pozorna, gdyż to sama przestrzeń (i jej współrzędne) się rozszerzają, co jest wyrażone w odpowiednim zakrzywieniu czaso-przestrzeni opisywanej w Ogólnej Teorii Względności. O samej prędkości światła też jest wygodniej myśleć jako o prędkości „przyczynowo-skutkowości”, wtedy łatwiej jest zrozumieć idee stożków świetlnych, etc. A jeszcze lepiej przyjąć c = 1 🙂
To niesamowite, że jedynie 39 cyfr liczby Pi wystarczy do osiągnięcia tak niezwykłej dokładności obliczeń dla obrzeży Obserwowalnego Wszechświata – 39 (=3.141592653589793238462643383279502884197) z poznanych 12 bilionów!
Na zakończenie filmik od Numberphile przedstawiający wyżej opisany problem.
Pozdrowienia,
Mariusz Gromada
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
W 17 wieku Newton i Leibniz skonstruowali podstawy rachunku różniczkowego i całkowego. Ich logika opierała się na wykorzystaniu wielkości nieskończenie małej w celu wyznaczenia powierzchni pod krzywą daną równaniem funkcji. Podejście to zakładało istnienie niezerowego elementu nieskończenie małego. Filozof Leibniz poszedł dalej, gdyż ponadto uważał, że cały świat jest zbudowany z tzw. monad, czyli z substancji, które nie mają żadnej postaci, ponieważ są niepodzielne, nie mogą być ani wytworzone ani unicestwione.
Jeszcze przed naszą erą Grecy z sukcesem stosowali metodę wyczerpywania do wyznaczenia pól powierzchni figur geometrycznych. Metoda ta wykorzystywała granice, nie wykorzystywała natomiast wielkości nieskończenie małej. Jednak z metody wyczerpywania wyrosła zasada Cavalieriego, odkryta przez Archimedesa, służąca do wyznaczania objętości brył, która opierała się na argumentacji wielkości niepodzielnej.
Intuicja podpowiada, że wielkość nieskończenie mała powinna być ekstremalnie mała, ale o niezerowym rozmiarze. W świecie praktycznym byłaby to np. wielkość mniejsza od najmniejszej teoretycznie możliwej wielkości do zmierzenia. Np. skala Plancka w fizyce dostarcza teoretycznej granicy pomiaru – nie ma możliwości skonstruowania przyrządu pomiarowego z błędem mniejszym niż skala Plancka, co nie oznacza, że poniżej skali Plancka nic nie istnieje.
 Zapraszam do ciekawego cyklu filmów przygotowanych przez Numberphile na temat wielkości nieskończenie małych.
Zapraszam do ciekawego cyklu filmów przygotowanych przez Numberphile na temat wielkości nieskończenie małych.
I na koniec jeszcze ciekawostka od MinutePhysics – Proof Without Words: The Circle.
Pozdrowienia,
Mariusz Gromada
 Ciekawostka od Numberphile pokazująca w jaki przedziwny sposób liczba PI jest ukryta w „ostrzu” zbioru Mandelbrota. Polecam!
Ciekawostka od Numberphile pokazująca w jaki przedziwny sposób liczba PI jest ukryta w „ostrzu” zbioru Mandelbrota. Polecam!
Pozdrowienia,
Mariusz Gromada
Zobacz również:
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
Kontynuując przeglądanie strony, wyrażasz zgodę na używanie przez nas plików cookies. więcej informacji
Aby zapewnić Tobie najwyższy poziom realizacji usługi, opcje ciasteczek na tej stronie są ustawione na "zezwalaj na pliki cookies". Kontynuując przeglądanie strony bez zmiany ustawień lub klikając przycisk "Akceptuję" zgadzasz się na ich wykorzystanie.