Wielkość nieskończenie – geneza powstania
W 17 wieku Newton i Leibniz skonstruowali podstawy rachunku różniczkowego i całkowego. Ich logika opierała się na wykorzystaniu wielkości nieskończenie małej w celu wyznaczenia powierzchni pod krzywą daną równaniem funkcji. Podejście to zakładało istnienie niezerowego elementu nieskończenie małego. Filozof Leibniz poszedł dalej, gdyż ponadto uważał, że cały świat jest zbudowany z tzw. monad, czyli z substancji, które nie mają żadnej postaci, ponieważ są niepodzielne, nie mogą być ani wytworzone ani unicestwione.
Jeszcze przed naszą erą Grecy z sukcesem stosowali metodę wyczerpywania do wyznaczenia pól powierzchni figur geometrycznych. Metoda ta wykorzystywała granice, nie wykorzystywała natomiast wielkości nieskończenie małej. Jednak z metody wyczerpywania wyrosła zasada Cavalieriego, odkryta przez Archimedesa, służąca do wyznaczania objętości brył, która opierała się na argumentacji wielkości niepodzielnej.
Wielkość nieskończenie mała a skala Plancka
Intuicja podpowiada, że wielkość nieskończenie mała powinna być ekstremalnie mała, ale o niezerowym rozmiarze. W świecie praktycznym byłaby to np. wielkość mniejsza od najmniejszej teoretycznie możliwej wielkości do zmierzenia. Np. skala Plancka w fizyce dostarcza teoretycznej granicy pomiaru – nie ma możliwości skonstruowania przyrządu pomiarowego z błędem mniejszym niż skala Plancka, co nie oznacza, że poniżej skali Plancka nic nie istnieje.
Wielkość nieskończenie mała – cykl filmów od Numberphile
 Zapraszam do ciekawego cyklu filmów przygotowanych przez Numberphile na temat wielkości nieskończenie małych.
Zapraszam do ciekawego cyklu filmów przygotowanych przez Numberphile na temat wielkości nieskończenie małych.
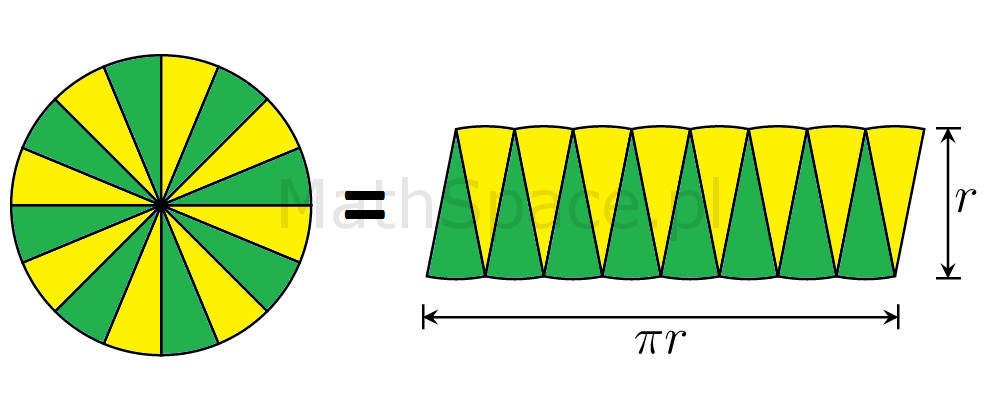
I na koniec jeszcze ciekawostka od MinutePhysics – Proof Without Words: The Circle.
Pozdrowienia,
Mariusz Gromada
