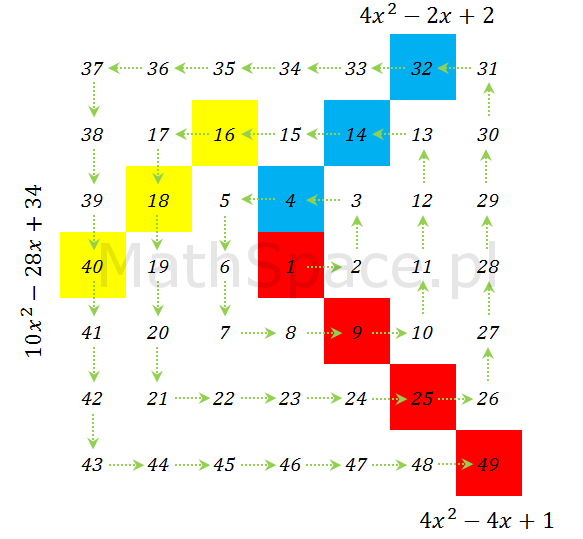
W części 1 wpisu na temat Spirali Ulama zaznaczyłem, że efekt wizualnego ułożenia liczb pierwszych na diagonalach spirali kwadratowej jest konsekwencją głównie dwóch własności:
- Na przekątnych są albo same liczby parzyste, albo same liczby nieparzyste, zatem tylko diagonale z liczbami nieparzystymi będą agregować liczby pierwsze;
- Niektóre diagonale zagęszczają bardziej liczby pierwsze niż inne, co wynika z zależności pomiędzy przekątnymi i funkcją kwadratową oraz faktem, że niektóre funkcje kwadratowe generują więcej liczb pierwszych niż inne.
Dzisiejszy tekst poświęcę przybliżeniu własności nr 2.
Wielomiany i rekurencja
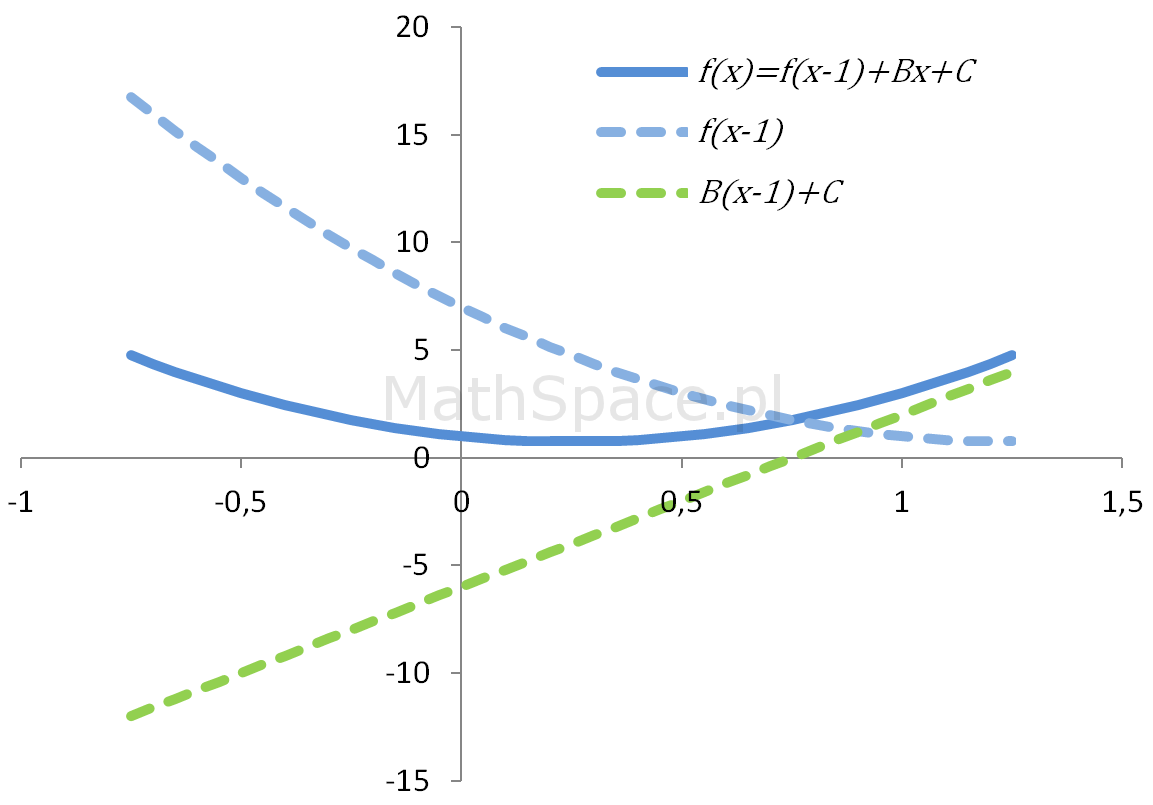
Dla wielomianów możemy zawsze podać ich postać rekurencyjną, Jest to własność mało znana, jednak dosyć prosta w uzasadnieniu. Pokażę to na przykładzie funkcji kwadratowej, jednocześnie wzbogacając cykl „Zabawy z rekurencją” 🙂
$$f(x) = ax^2+bx+c$$
Rozważmy następnie równanie
$$f(x+1)=f(x)+Bx+C$$
Podstawiając i upraszczając…
$$a(x+1)^2+b(x+1)+c=ax^2+bx+c+Bx+C$$
$$ax^2+2ax+a+bx+b+c=ax^2+bx+c+Bx+C$$
$$2ax+a+b=Bx+C$$
$2a=B$ oraz $a+b=C$
otrzymujemy
$a=\frac{B}{2}$ oraz $b=C-a$
Następnie analizując $f(1)$ mamy
$f(1)=a+b+c$ zatem $c=f(1)-a-b$
$$c=f(1)-a-(C-a)=f(1)-C$$
Wniosek: jeśli znana jest relacja rekurencyjna $f(x+1)=f(x)+Bx+C$ oraz znamy wartość $f(1)$ to jesteśmy w stanie jednoznacznie wskazać równanie kwadratowe $ax^2+bx+c$ spełniające daną zależność rekurencyjna, gdzie
$a=\frac{B}{2}$, $b=C-a$, $c=f(1)-C$
Uogólnienia dokonujemy na bazie dwumianu Newtona
$$(x+1)^n = {n\choose 0}x^n+{n\choose 1}x^{n-1}+{n\choose 2}x^{n-2}+\ldots+{n\choose {n-1}}x+{n\choose n}$$
Funkcja kwadratowa i linie proste / przekątne na spirali Ulama
Poniżej spróbuję pokazać w jaki sposób „nawijanie prostej na kwadrat” sprawia, że parabole w efekcie otrzymują kształt linii prostych.
Przykład 1 – Pionowa prosta
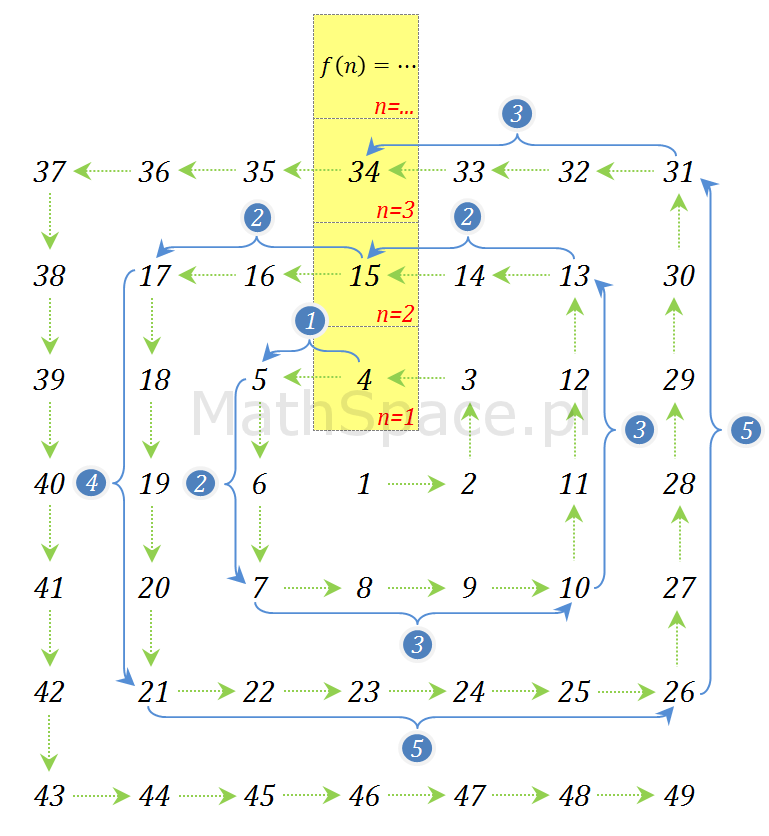
Zapisujemy zależność rekurencyjną
$$f(1)=4$$
$$f(2)=f(1)+1+2+3+3+2$$
$$f(3)=f(2)+2+3+5+5+3$$
$$\ldots$$
$$f(n+1)=f(n)+n+2n+(2n+1)+(2n+1)+(n+1)$$
$$f(n+1)=f(n)+8n+3$$
Teraz, korzystając z wyprowadzonego wcześniej wzoru, wyznaczamy współczynniki a, b, c funkcji kwadratowej spełniającej $f(n+1)=f(n)+8n+3$.
$a=\frac{8}{2}=4$, $b=3-4=-1$, $c=4-3=1$
$$f(n)=4n^2-n+1$$
Dla testu czy wszystko jest ok sami podstawcie $n=1,2,3\ldots$
Przykład 2 – Przekątna (linia diagonalna)

Ponownie zapisujemy zależność rekurencyjną, tym razem nieco prostszą.
$$f(1)=3$$
$$f(2)=f(1)+2+2+3+3$$
$$f(3)=f(2)+4+4+5+5$$
$$\ldots$$
$$f(n+1)=f(n)+n+2n+2n+(2n+1)+(2n+1)$$
$$f(n+1)=f(n)+8n+2$$
Korzystając ze znanego wzoru wyznaczamy a, b, c dla $f(n+1)=f(n)+8n+2$.
$a=\frac{8}{2}=4$, $b=2-4=-2$, $c=3-2=1$
$$f(n)=4n^2-2n+1$$
Przykład: funkcja $n^2+n+41$ generująca liczby pierwsze
Wielomian $n^2+n+41$ jest funkcją „często generującą” liczby pierwsze. W tym przypadku dla każdego $n=0,1,\ldots,39$ wynik jest zawsze liczbą pierwszą. Poniżej tabela prezentująca zestawienie dla $n$ z zakresu od $0$ do $100$.
| n | n^2+n+41 | Czy liczba pierwsza? |
|---|---|---|
| 0 | 41 | 1 |
| 1 | 43 | 1 |
| 2 | 47 | 1 |
| 3 | 53 | 1 |
| 4 | 61 | 1 |
| 5 | 71 | 1 |
| 6 | 83 | 1 |
| 7 | 97 | 1 |
| 8 | 113 | 1 |
| 9 | 131 | 1 |
| 10 | 151 | 1 |
| 11 | 173 | 1 |
| 12 | 197 | 1 |
| 13 | 223 | 1 |
| 14 | 251 | 1 |
| 15 | 281 | 1 |
| 16 | 313 | 1 |
| 17 | 347 | 1 |
| 18 | 383 | 1 |
| 19 | 421 | 1 |
| 20 | 461 | 1 |
| 21 | 503 | 1 |
| 22 | 547 | 1 |
| 23 | 593 | 1 |
| 24 | 641 | 1 |
| 25 | 691 | 1 |
| 26 | 743 | 1 |
| 27 | 797 | 1 |
| 28 | 853 | 1 |
| 29 | 911 | 1 |
| 30 | 971 | 1 |
| 31 | 1033 | 1 |
| 32 | 1097 | 1 |
| 33 | 1163 | 1 |
| 34 | 1231 | 1 |
| 35 | 1301 | 1 |
| 36 | 1373 | 1 |
| 37 | 1447 | 1 |
| 38 | 1523 | 1 |
| 39 | 1601 | 1 |
| 40 | 1681 | 0 |
| 41 | 1763 | 0 |
| 42 | 1847 | 1 |
| 43 | 1933 | 1 |
| 44 | 2021 | 0 |
| 45 | 2111 | 1 |
| 46 | 2203 | 1 |
| 47 | 2297 | 1 |
| 48 | 2393 | 1 |
| 49 | 2491 | 0 |
| 50 | 2591 | 1 |
| 51 | 2693 | 1 |
| 52 | 2797 | 1 |
| 53 | 2903 | 1 |
| 54 | 3011 | 1 |
| 55 | 3121 | 1 |
| 56 | 3233 | 0 |
| 57 | 3347 | 1 |
| 58 | 3463 | 1 |
| 59 | 3581 | 1 |
| 60 | 3701 | 1 |
| 61 | 3823 | 1 |
| 62 | 3947 | 1 |
| 63 | 4073 | 1 |
| 64 | 4201 | 1 |
| 65 | 4331 | 0 |
| 66 | 4463 | 1 |
| 67 | 4597 | 1 |
| 68 | 4733 | 1 |
| 69 | 4871 | 1 |
| 70 | 5011 | 1 |
| 71 | 5153 | 1 |
| 72 | 5297 | 1 |
| 73 | 5443 | 1 |
| 74 | 5591 | 1 |
| 75 | 5741 | 1 |
| 76 | 5893 | 0 |
| 77 | 6047 | 1 |
| 78 | 6203 | 1 |
| 79 | 6361 | 1 |
| 80 | 6521 | 1 |
| 81 | 6683 | 0 |
| 82 | 6847 | 0 |
| 83 | 7013 | 1 |
| 84 | 7181 | 0 |
| 85 | 7351 | 1 |
| 86 | 7523 | 1 |
| 87 | 7697 | 0 |
| 88 | 7873 | 1 |
| 89 | 8051 | 0 |
| 90 | 8231 | 1 |
| 91 | 8413 | 0 |
| 92 | 8597 | 1 |
| 93 | 8783 | 1 |
| 94 | 8971 | 1 |
| 95 | 9161 | 1 |
| 96 | 9353 | 0 |
| 97 | 9547 | 1 |
| 98 | 9743 | 1 |
| 99 | 9941 | 1 |
| 100 | 10141 | 1 |
Po więcej przykładów odsyłam do artykułu „Prime-Generating Polynomial”.
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

 następnie usuwając pozostałe.
następnie usuwając pozostałe. W tym momencie
W tym momencie