Jestem pewien, że wzór na pole powierzchni trójkąta, tj. $P=\frac{1}{2}ah$, jest znany niemal wszystkim 🙂 Dzieci, będąc we wczesnym wieku szkolnym, poznają podstawy geometrii, w tym długości obwodów i pola powierzchni figur płaskich. Jeśli interesuje cię dlaczego pole powierzchni trójkąta zależy od długości jego podstawy i wysokości na nią opadającej, to jest to wpis dla Ciebie 🙂 Jednocześnie wzbogacam cykl „Dlaczego?”. Zaczynamy!
Pole powierzchni trójkąta – wzór
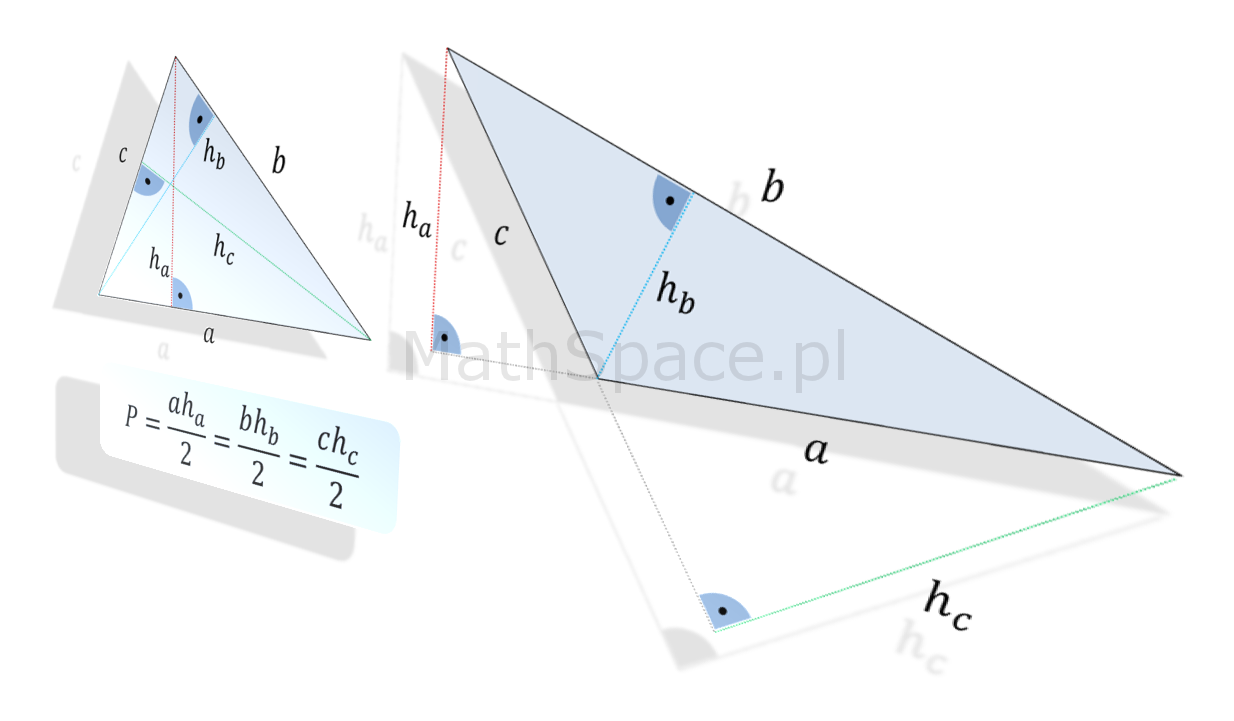
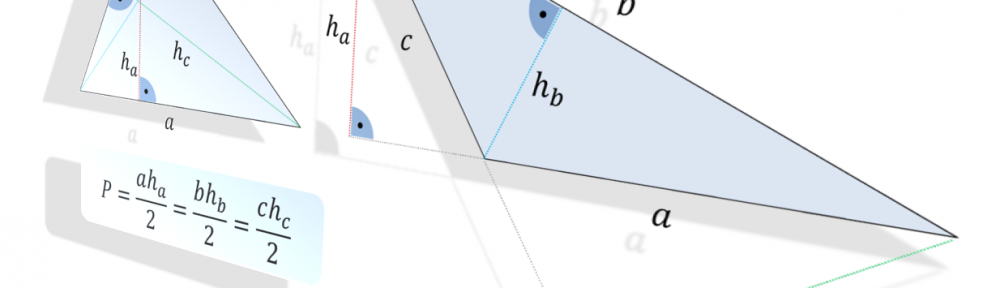
Wzór na pole powierzchni trójkąta, choć prosty, to na pierwszy rzut oka nie jest zbyt intuicyjny (no może poza przypadkiem trójkąta prostokątnego). Oto, w jakiś magiczny sposób, dla każdej podstawy, iloczyny ich długości i długości wysokości na nie opadających, są sobie równe – i więcej – określą pole powierzchni ograniczonej trójkątem 🙂
$$P=\frac{ah_a}{2}=\frac{bh_b}{2}=\frac{ch_c}{2}$$
Pole powierzchni trójkąta – dowód przez animację 🙂 – przypadek 1
Przypadek 1: kiedy wysokość trójkąta „opada” na jego podstawę.

Pole powierzchni trójkąta – dowód przez animację 🙂 – przypadek 2
Przypadek 2: kiedy wysokość trójkąta „opada” poza jego podstawą.

Pole powierzchni trójkąta – dowód nieco bardziej formalny
Trójkąt prostokątny: przypadek oczywisty, nie wymaga wyprowadzenia 🙂
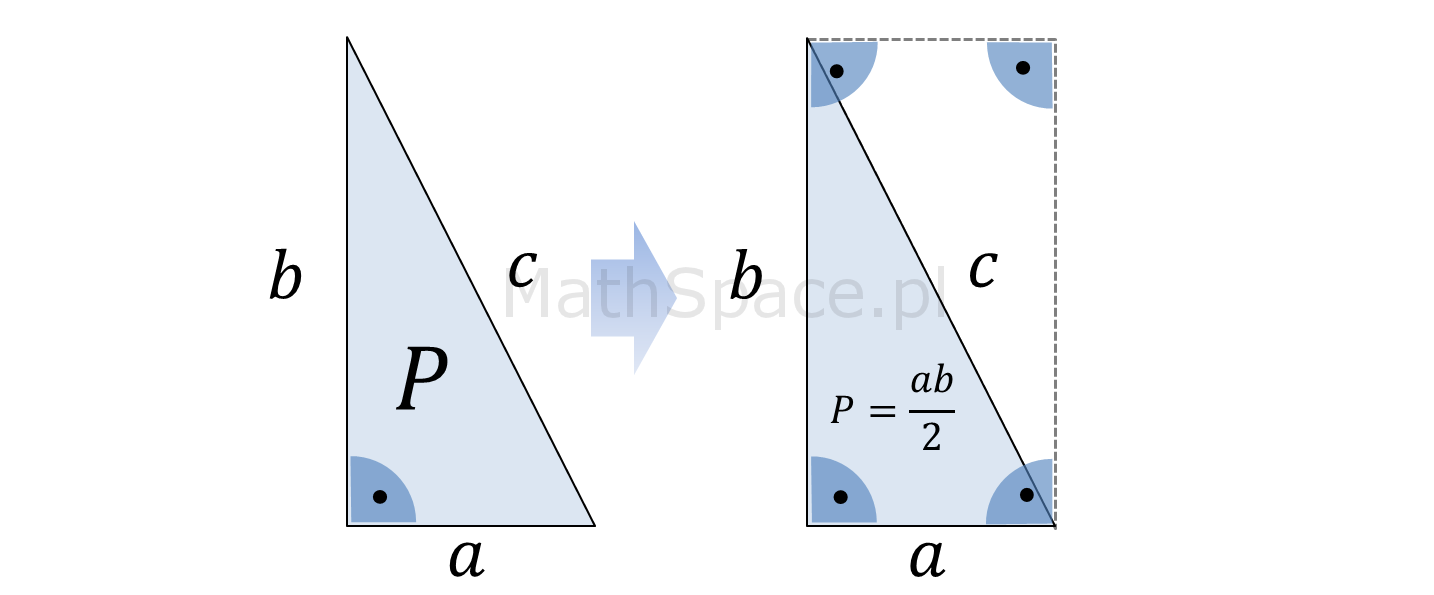
$$P=\frac{ab}{2}$$
Przypadek 1: kiedy wysokość trójkąta „opada” na jego podstawę.
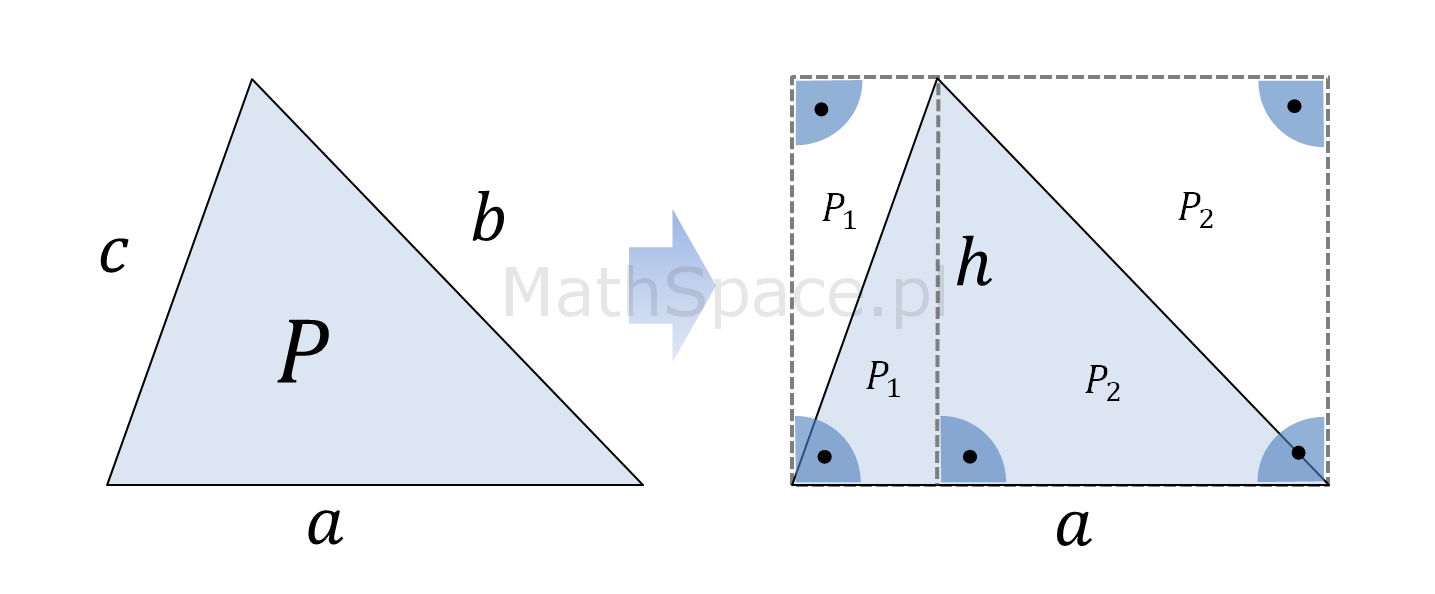
Wyprowadzenie wzoru:
$$P=P_1+P_2$$
$$2P_1+2P_2=ah$$
$$P_1+P_2=\frac{ah}{2}$$
$$P=\frac{ah}{2}$$
Przypadek 2: kiedy wysokość trójkąta „opada” poza jego podstawą.
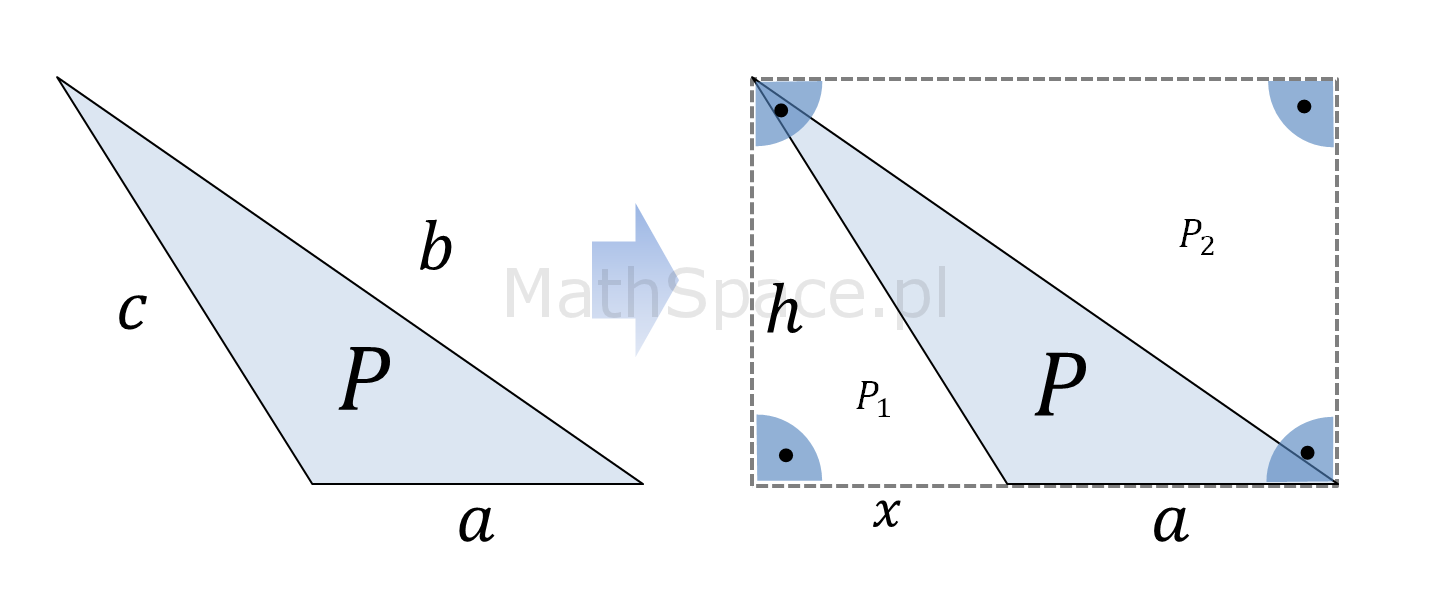
Wyprowadzenie wzoru:
$$P+P_1=P_2$$
$$P=P_2-P_1$$
$$P_1=\frac{xh}{2}$$
$$P_2=\frac{(a+x)h}{2}=\frac{ah}{2}+\frac{xh}{2}$$
$$P=P_2-P_1=\frac{ah}{2}+\frac{xh}{2}-\frac{xh}{2}=\frac{ah}{2}$$
$$P=\frac{ah}{2}$$
Koniec na dziś 🙂
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.