Inverse Transform Sampling to typowy sposób generowania liczb pseudolosowych z zadanego rozkładu, który opiera się na funkcji odwrotnej $F^{-1}$ do dystrybuanty $F$ tego rozkładu. Procedura jest banalna, wystarczy wylosować $Y\sim U(0,1)$ i zwrócić $F^{-1}(Y)$. Niestety nie zawsze łatwe jest wyznaczenie jawnej postaci dystrybuanty, tym bardziej dotyczy to funkcji do niej odwrotnej. Dla przykładu – powszechny rozkład normalny charakteryzuje się funkcją gęstości w postaci „elementarnej”, natomiast jego dystrybuanta (i funkcja do niej odwrotna) wymagają zastosowania funkcji specjalnych – w tym przypadku funkcji błędu Gaussa.

Kiedyś kolega (pozdrowienia Marcin!) pokazał mi nieskomplikowany sposób generacji liczb losowych z rozkładu opisanego histogramem. Zwyczajnie „kładziemy” (skalując) słupki histogramu na odcinek $(0,1)$, losujemy $X\sim U(0,1)$, weryfikujemy „do którego słupka wpadło X”, zwracamy „właśnie ten słupek”. Genialne w swojej prostocie, i działa. Histogram to dyskretna reprezentacja rozkładu, dlatego postanowiłem metodę uogólnić na klasę rozkładów ciągłych opisanych zadaną funkcją gęstości. Otrzymaną metodę nazwałem „MaCDRG-yver” 🙂

MaCDRG-yver – czyli Monte Carlo Density based Random Generator

Generacja liczb losowych metodą Monte Carlo? Brzmi nieźle 🙂

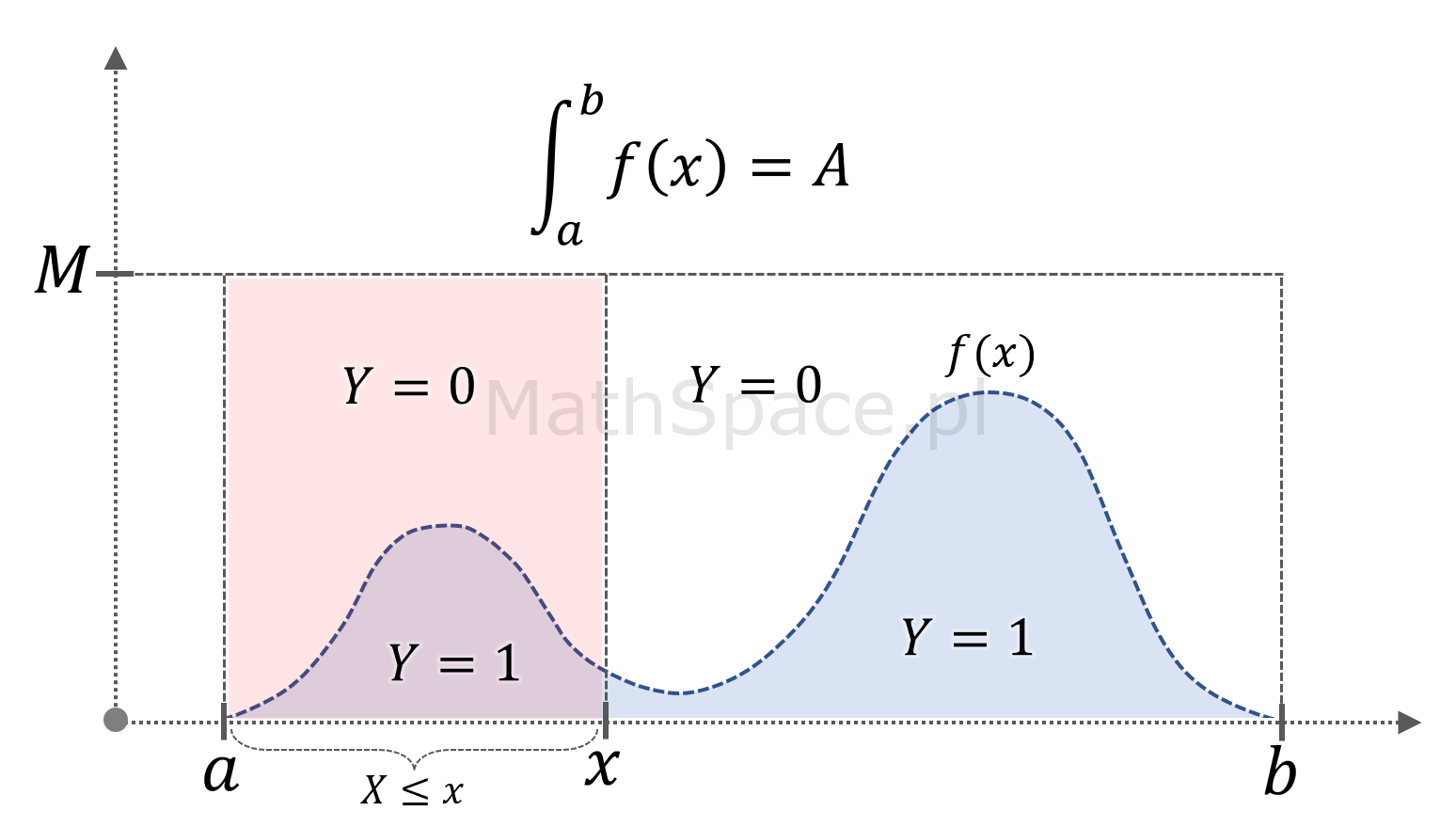
Twierdzenie: jeśli funkcja $f:[a,b]\to\mathbb{R}$ jest nieujemna, ograniczona oraz spełnia warunki

$$\displaystyle\int_a^bf(x)dx=A>0$$

oraz

$$f(x)\leq M$$ dla $$x\in[a,b]$$

to zmienna losowa $\big(X~|~Y=1\big)$, gdzie

$$X\sim U\big(a,b\big)$$

$$Y=\begin{cases}1&&\text{dla}&&Z\leq f(X)\\0&&\text{dla}&&Z>f(X)\end{cases}$$

$$Z\sim U\big(0,M\big)$$

pochodzi z rozkładu warunkowego opisanego funkcją gęstości $\frac{1}{A}f(x)$, tzn.

$$P\Big(X\leq x~|~Y=1\Big)=\frac{1}{A}\displaystyle\int_a^xf(t)dt$$

dla $x\in[a,b]$.

Dowód: korzystając z prawdopodobieństwa warunkowego

$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

$$P(B|A)=\frac{P(B\cap A)}{P(A)}$$

możemy zapisać, że

$$P(A\cap B)=P(A|B)P(B)=P(B|A)P(A)$$

wtedy

$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

zatem

$$P\Big(X\leq x~|~Y=1\Big)=\frac{P\big(Y=1~|~X\leq x\big)P\big(X\leq x\big)}{P\big(Y=1\big)}=…$$

ale

$$P\big(Y=1\big)=\frac{A}{M(b-a)}$$

$$P\big(X\leq x\big)=\frac{x-a}{b-a}$$

$$P\big(Y=1~|~X\leq x\big)=\frac{1}{M(x-a)}\displaystyle\int_a^xf(t)dt$$

podstawiając

$$…=\Bigg(\frac{1}{M(x-a)}\displaystyle\int_a^xf(t)dt\Bigg)\Bigg(\frac{x-a}{b-a}\Bigg)\Bigg(\frac{A}{M(b-a)}\Bigg)^{-1}=$$

$$=\frac{M(b-a)(x-a)}{M(x-a)(b-a)A}\displaystyle\int_a^xf(t)dt$$

ostatecznie

$$P\Big(X\leq x~|~Y=1\Big)=\frac{1}{A}\displaystyle\int_a^xf(t)dt$$

Uwaga: precyzyjność twierdzenia wymaga założenia, aby funkcja $f(x)$ była dodatkowo borelowska. Podyktowane jest to konstrukcją probabilistyki, gdzie sama zmienna losowa definiowana jest jako funkcja rzeczywista mierzalna przy założeniu sigma-ciała zbiorów borelowskich w $\mathbb{R}$. Funkcja gęstości przyporządkowuje prawdopodobieństwo na bazie całki / miary Lebesgue’a, natomiast zmienna losowa „dokonuje transportu” miary probabilistycznej i zdarzeń z „abstrakcyjnej” przestrzeni do przestrzeni rzeczywistej, zachowując „strukturę mierzalności” w ograniczeniu do zbiorów borelowskich w $\mathbb{R}$.

Wniosek #1: jeśli $f(x)$ jest taką gęstością rozkładu prawdopodobieństwa, że

$$\displaystyle\int_a^bf(x)dx=1$$

to zmienna losowa $\big(X~|~Y=1\big)$ pochodzi z rozkładu o gęstości $f(x)$.

Wniosek #2: posiadając funkcję gęstości $f(x)$, spełniającą powyższe warunki, możliwe jest wygenerowanie liczb pseudolosowych z rozkładu o gęstości $f(x)$ stosując poniższe kroki:

1. Wylosuj $X\sim U(a,b)$;
2. Wylosuj $Z\sim U(0,M)$;
3. Jeśli $Z\leq f(X)$, zwróć $X$ jako liczbę pseudolosową;
4. Jeśli $Z>f(X)$, wróć do kroku $1$.

Należy się starać, aby ograniczenie $M$ było możliwie małe – ma to bezpośredni wpływ na liczbę iteracji niezbędnych do zwrócenia liczby losowej.

Wniosek #3: generacja liczb pseudolosowych nie wymaga, aby $f(x)$ była „znormalizowana” do $\displaystyle\int_a^bf(x)dx=1$.

MaCDRG-yver w praktyce

Do testów wykorzystałem pakiet MathParser.org-mXparser.

$$f(x)=\sin^2x$$

$a=-2\pi$      $b=2\pi$      $M=1$

/*
* Funkcja f(x)
*/
Function f = new Function("f(x) = sin(x)^2");
/*
* Definicja algorytmu MaCDRG-yver - rekurencja
*/
Function MaCDRG = new Function("MaCDRG(a,b,M,x) = if( rUni(0,M) <= f(x), x, MaCDRG(a,b,M, rUni(a,b) ) )", f);
/*
* Definicja zmiennej losowej
*/
Argument X = new Argument("X = MaCDRG( -2*pi, 2*pi, 1, rUni(-2*pi, 2*pi) )", MaCDRG);
/*
* Wygenerowanie kilku losowych liczb
*/
mXparser.consolePrintln(X.getArgumentValue());
mXparser.consolePrintln(X.getArgumentValue());
mXparser.consolePrintln(X.getArgumentValue());
mXparser.consolePrintln(X.getArgumentValue());
mXparser.consolePrintln(X.getArgumentValue());

Wynik

[mXparser-v.4.1.1] 1.0189765202912655
[mXparser-v.4.1.1] -1.7474018879236324
[mXparser-v.4.1.1] -5.455276346221208
[mXparser-v.4.1.1] 3.880570732065584
[mXparser-v.4.1.1] 4.418850002784142

Poniżej animacja od 5 tys. do 100 tys. losowań.

Jestem przekonany, że mi się to kiedyś przyda 🙂 Mam nadzieję, że Wam również!

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa