Rozkład jednostajny na odcinku $(0,1)$, chyba najprostszy z możliwych rozkładów ciągłych, z pozoru niezbyt interesujący, a jednak 🙂 Dziś ciekawostka wiążąca rozkład sumy rozkładów jednostajnych z liczbą Eulera e.

Rozkład jednostajny ciągły na odcinku (a,b)

Rozkład jednostajny ciągły na odcinku $(a,b)$ jest opisany poniższą funkcją gęstości.

$$f(x)=\begin{cases}\frac{1}{b-a}&&\text{dla }a\leq x\leq b\\0&&\text{w p.p.}\end{cases}$$

Pisząc $X\sim U(a,b)$ oznaczamy, że zmienna losowa $X$ ma rozkład jednostajny ciągły na odcinku $(a,b)$. Jest to rozkład ciągły, zatem przyjęcie wartości $0$ lub $\frac{1}{b-a}$ w punktach $x=a$ i $x=b$ jest umowne i nie ma zwykle wpływu na własności i rozważania.

Rozkład jednostajny przypisuje prawdopodobieństwo zdarzenia na bazie jego „rozmiaru”, a dokładniej rozmiaru tej części, która znajduje się w odcinku $(a,b)$.

Jeśli $X\sim U(a,b)$ to:

• $\rm E X=\frac{a+b}{2}$
• $\rm Mediana(X)=\frac{a+b}{2}$
• $\rm Var(X)=\frac{(b-a)^2}{12}$

Rozkład Irwina-Halla – czyli suma rozkładów jednostajnych ciągłych

Dla $n$ niezależnych zmiennych losowych pochodzących z rozkładu jednostajnego ciągłego na odcinku $(0,1)$

$$X_1,X_2,\ldots,X_n\sim U(0,1)$$

można zdefiniować zmienną losową będącą ich sumą

$$X=X_1+X_2+\ldots+X_n=\displaystyle\sum_{i=1}^nX_i$$

O zmiennej $X$ mówimy, że pochodzi z rozkładu Irwina-Halla, co zapisujemy

$$X\sim IH(n)$$

Funkcja gęstości rozkładu Irwina-Halla dana jest poniższym wzorem (wyprowadzenie pomijam, gdyż nie jest to główny temat wpisu).

$$f(x)=\frac{1}{(n-1)!}\displaystyle\sum_{k=0}^{\lfloor x\rfloor}(-1)^k{n\choose k}(x-k)^{n-1}$$

Jeśli $X\sim IH(n)$ to:

• $\rm E X=\frac{n}{2}$
• $\rm Mediana(X)=\frac{n}{2}$
• $\rm Var(X)=\frac{n}{12}$

Ciekawostka: rozkład sumy rozkładów jednostajnych przypomina „kształtem” rozkład normalny. W praktyce możliwe jest „przybliżone” wygenerowanie liczb z rozkładu normalnego korzystając z niezbyt „długiej” sumy liczb z rozkładu jednostajnego, odpowiednio przesuwając i skalując wynik.

Jak „standaryzować” funkcję gęstości?

• $f(x)$ – gęstość rozkładu – znana
• $EX=\mu$ – znane
• $Var(X)=\sigma^2$ – znane

Poszukujemy nowej gęstości rozkładu prawdopodobieństwa

$$g(x)=af(bx+c)$$

Zaczynamy od warunku na gęstość – tzn. „masa prawdopodobieństwa” to 1.

$$\displaystyle\int_\mathbb{R}g(x)dx=1$$

$$\displaystyle\int_\mathbb{R}g(x)dx=\displaystyle\int_\mathbb{R}af(bx+c)dx=$$

$$=\begin{bmatrix}t=bx+c\\\frac{dt}{b}=dx\end{bmatrix}=$$

$$=\displaystyle\int_\mathbb{R}af(t)\frac{dt}{b}=\frac{a}{b}\displaystyle\int_\mathbb{R}f(t)dt=\frac{a}{b}\cdot 1$$

$$\frac{a}{b}=1$$ zatem $$a=b$$

Zapisujemy

$$g(x)=af(ax+c)$$

Stosujemy warunek na wartość oczekiwaną równą „0”

$$0=\displaystyle\int_\mathbb{R}xg(x)dx=\displaystyle\int_\mathbb{R}xaf(ax+c)dx=$$

$$=\begin{bmatrix}t=ax+c\\\frac{dt}{a}=dx\\x=\frac{t-c}{a}\end{bmatrix}=$$

$$=\displaystyle\int_\mathbb{R}\frac{t-c}{a}af(t)\frac{dt}{a}=\frac{1}{a}\displaystyle\int_\mathbb{R}(t-c)f(t)dt=$$

$$=\frac{1}{a}\Bigg[\displaystyle\int_\mathbb{R}tf(t)dt-c\displaystyle\int_\mathbb{R}f(t)dt\Bigg]=\frac{1}{a}(\mu-c)$$

$$\frac{\mu-c}{a}=0$$

$$\mu-c=0$$ zatem $$c=\mu$$

Zapisujemy

$$g(x)=af(ax+\mu)$$

Stosujemy warunek na wariancję równą „1”

$$1=\displaystyle\int_\mathbb{R}x^2g(x)dx-\Bigg(~~\underbrace{\displaystyle\int_\mathbb{R}xg(x)dx}_{0}~~\Bigg)^2=\displaystyle\int_\mathbb{R}x^2af(ax+\mu)dx$$

$$=\begin{bmatrix}t=ax+\mu\\\frac{dt}{a}=dx\\x=\frac{t-\mu}{a}\end{bmatrix}=$$

$$=\displaystyle\int_\mathbb{R}\Bigg(\frac{t-\mu}{a}\Bigg)^2af(t)\frac{dt}{a}=\frac{1}{a^2}\displaystyle\int_\mathbb{R}\Big(t^2-2t\mu+\mu^2\Big)f(t)dt=$$

$$=\frac{1}{a^2}\Bigg[\displaystyle\int_\mathbb{R}t^2f(t)dt-2\mu\displaystyle\int_\mathbb{R}tf(t)dt+\mu^2\displaystyle\int_\mathbb{R}f(t)dt\Bigg]=…$$

ale

$$\sigma^2=\displaystyle\int_\mathbb{R}t^2f(t)dt-\Bigg(\displaystyle\int_\mathbb{R}tf(t)dt\Bigg)^2=\displaystyle\int_\mathbb{R}t^2f(t)dt-\mu^2$$

więc

$$\displaystyle\int_\mathbb{R}t^2f(t)dt=\sigma^2+\mu^2$$

$$…=\frac{1}{a^2}\Big(\sigma^2+\mu^2-2\mu^2+\mu^2\Big)=\frac{\sigma^2}{a^2}$$

$$\frac{\sigma^2}{a^2}=1$$

$$a^2=\sigma^2$$

$$a=\sigma$$

Funkcja gęstości jest funkcją dodatnią, dlatego odrzucamy $$a=-\sigma$$.

Ostatecznie

$$g(x)=\sigma f(\sigma x+\mu)$$

Podsumowując, jeśli zmienna losowa $X$ pochodzi z rozkładu opisanego funkcją gęstości $f(x)$, o wartości oczekiwanej $EX=\mu$ oraz skończonej wariancji $Var(X)=\sigma^2$, to standaryzowana zmienna losowa

$$\frac{X-\mu}{\sigma}$$

pochodzi z rozkładu opisanego gęstością

$$\sigma f(\sigma x+\mu)$$

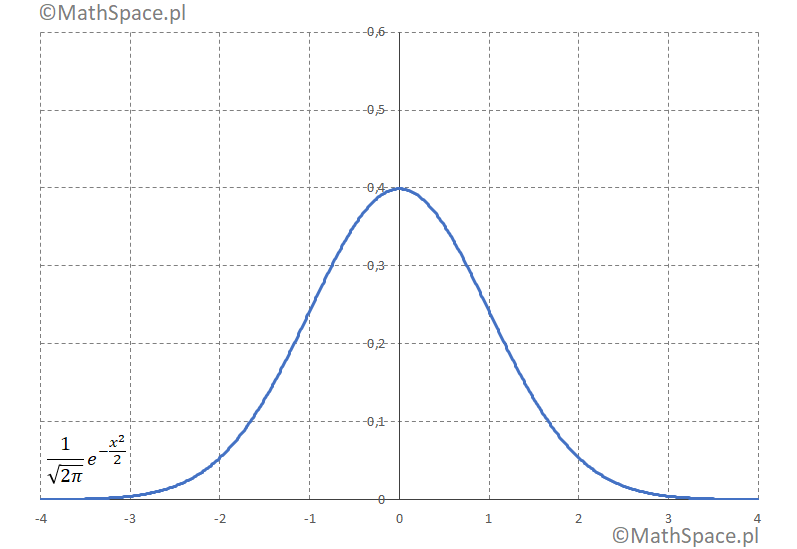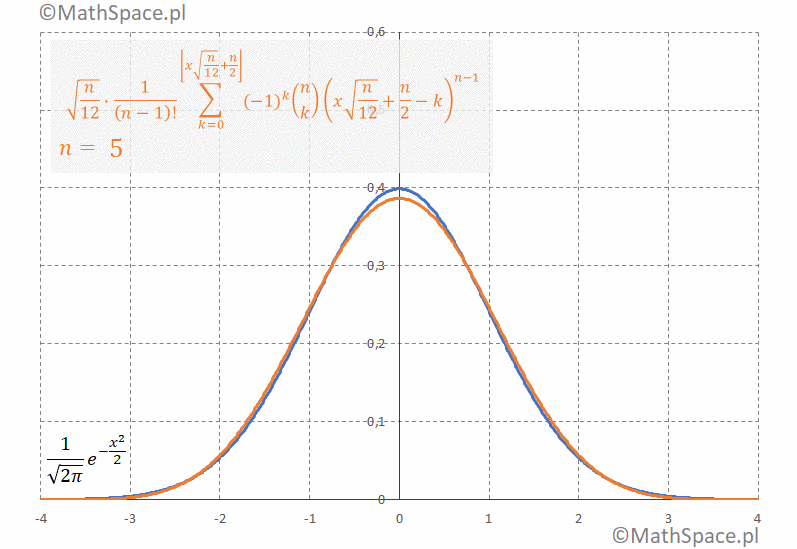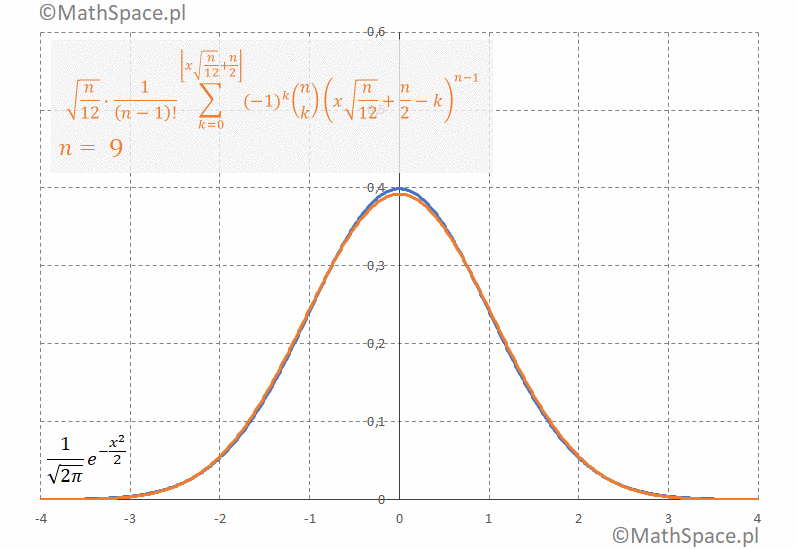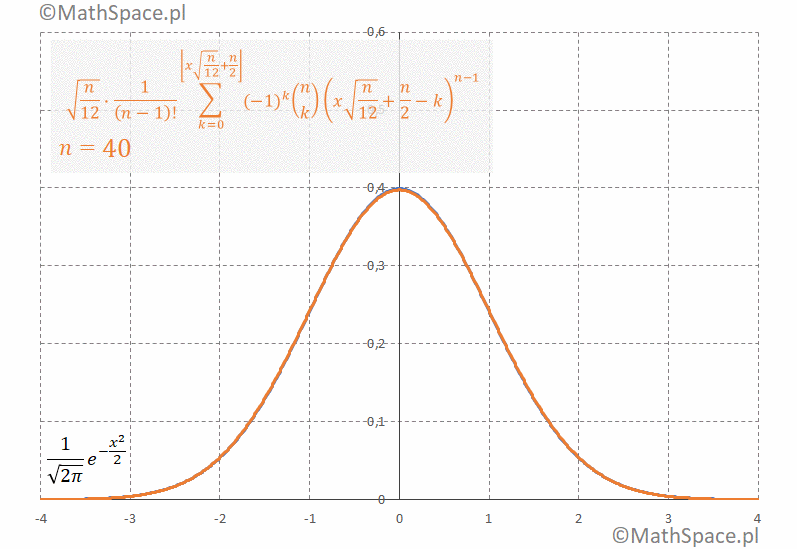
Jakość przybliżenia rozkładu normalnego na bazie sumy rozkładów jednostajnie ciągłych

Porównany dwie funkcje gęstości

1. Gęstość rozkładu $N(0,1)$ tzw. standardowego rozkładu normalnego

$$\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$$

2. Standaryzowana gęstość rozkładu Irwina-Halla

$$\sqrt{\frac{n}{12}}\frac{1}{(n-1)!}\displaystyle\sum_{k=0}^{\bigg\lfloor x\sqrt{\frac{n}{12}}+\frac{n}{2}\bigg\rfloor}(-1)^k{n\choose k}\Bigg(x\sqrt{\frac{n}{12}}+\frac{n}{2}-k\Bigg)^{n-1}$$

Poniżej animacja obrazująca bardzo szybką zbieżność gęstości do $N(0,1)$

Gdzie ten Euler?

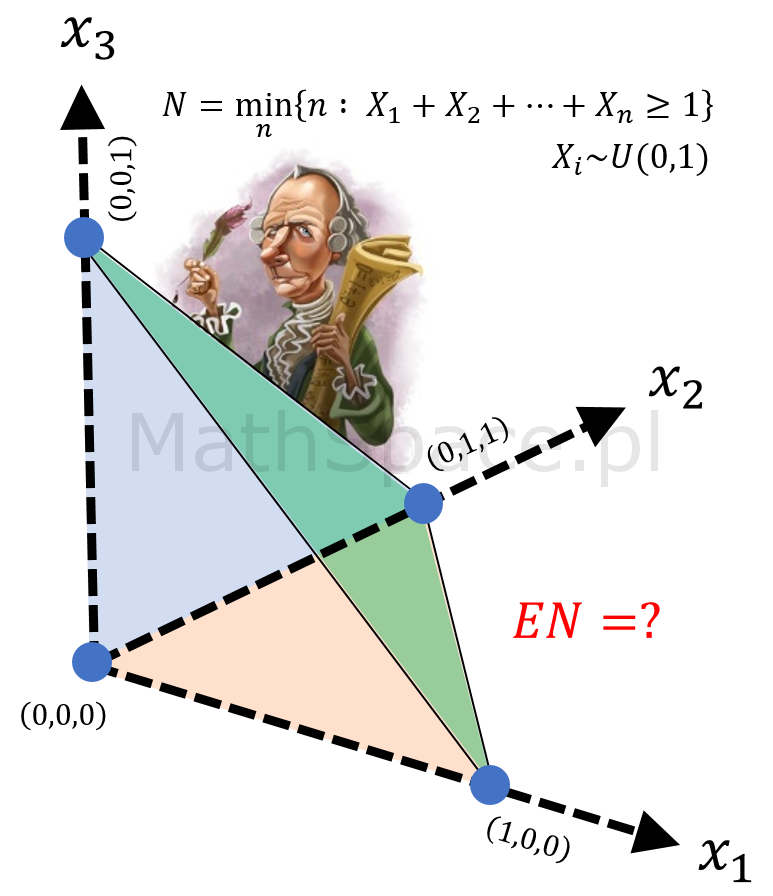
Korzystając z centralnego twierdzenia granicznego, niemal na bazie każdego rozkładu, jesteśmy w stanie wygenerować liczby losowe przybliżające rozkład normalny – zatem, w tym sensie, rozkład Irwina-Halla niczym się nie wyróżnia. Jest w nim jednak coś specjalnego – szczególne powiązanie z liczbą Eulera e. W dalszej części tekstu będą rozważał minimalną liczbę losowań z rozkładu $U(0,1)$ niezbędnych do przekroczenia pewnej ustalonej wartości – np. losujemy, sumujemy, kończymy po otrzymaniu 1 lub więcej.

Minimalna liczba losowań z $U(0,1)$ potrzebna do przekroczenia liczby $1$ (przekroczenie osiągane sumując wyniki)

Przez $N_1$ oznaczamy taką zmienną losową powstającą na bazie n niezależnych zmiennych losowych z rozkładu jednostajnego ciągłego $U(0,1)$, że

$$N_1=\min\Big\{n~:~X_1+X_2+\ldots+X_n\geq 1\Big\}$$

$$X_i\sim U(0,1)$$

Jeśli $N_1=n$ to $X_1+X_2+\ldots+X_n\geq 1$ oraz $X_1+X_2+\ldots+X_{n-1}<1$.

Analogicznie tworzymy zmienną losową $N_a$

$$N_a=\min\Big\{n~:~X_1+X_2+\ldots+X_n\geq a\Big\}$$

$$X_i\sim U(0,1)$$

Jeśli $N_a=n$ to $X_1+X_2+\ldots+X_n\geq a$ oraz $X_1+X_2+\ldots+X_{n-1}<a$.

Wartość oczekiwania zmiennej losowej $N_1$?

Spostrzeżenie #1: $N_1$ jest zmienną losową dyskretną o niezbyt „przyjemnej” w analizie funkcji masy prawdopodobieństwa.

$pmf_{N_1}(n)$ – oznacza prawdopodobieństwo, że dokładnie $n$ losowań wystarczy do przekroczenia jedności, natomiast $n-1$ losowań to zbyt mało.

Spostrzeżenie #2: dystrybuanta rozkładu, z którego pochodzi $N_1$, jest łatwiejsza w analizie, gdyż podaje prawdopodobieństwo, że n losowań wystarczy (bez żadnych dodatkowych warunków).

$$F_{N_1}(n)=P\Big(N_1\leq n\Big)$$

Spostrzeżenie #3: zmienna losowa $N_1$ przyjmuje wartości nieujemne, dlatego jej wartość oczekiwaną można wyrazić za pomocą dystrybuanty (sumując pole powierzchni ponad dystrybuantą).

$$EN_1=\displaystyle\sum_{n=0}^\infty\Big(1-F_{N_1}(n)\Big)$$

Spostrzeżenie #4: $P\Big(N_1=0\Big)=0$ oraz $P\Big(N_1=1\Big)=0$ zatem $F_{N_1}(0)=0$ oraz $F_{N_1}(1)=0$, wtedy

$$EN_1=1+1+\displaystyle\sum_{n=2}^\infty\Big(1-F_{N_1}(n)\Big)$$

Spostrzeżenie #5: jeśli $F_{N_1}(n)$ oznacza prawdopodobieństwo, że n losowań wystarczy, to $1-F_{N_1}(n)$ oznacza prawdopodobieństwo, że n losowań to zbyt mało.

Spostrzeżenie #6: w przestrzeni $\mathbb{R}^n$ zdarzenie, że n losowań to zbyt mało, reprezentowane jest przez zbiór

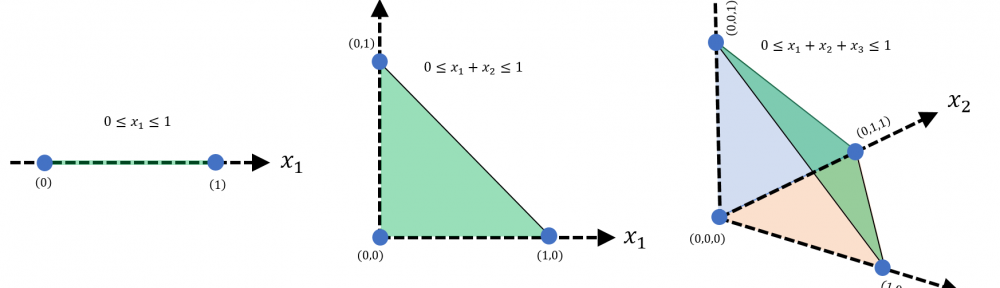
$$\bigg\{(x_1,x_2,\ldots,x_n)\in\mathbb{R}^n~:~0\leq x_1+x_2+\ldots+x_n<1\bigg\}$$

Bez wpływu na wartość prawdopodobieństwa (dodajemy jedynie „górną powierzchnię”) możemy zapisać

$$\bigg\{(x_1,x_2,\ldots,x_n)\in\mathbb{R}^n~:~0\leq x_1+x_2+\ldots+x_n\leq 1\bigg\}$$

Spostrzeżenie #7: graficzna reprezentacja ww. zbiorów dla przestrzeni 1, 2 i 3 wymiarowej ujawnia prawidłowość.

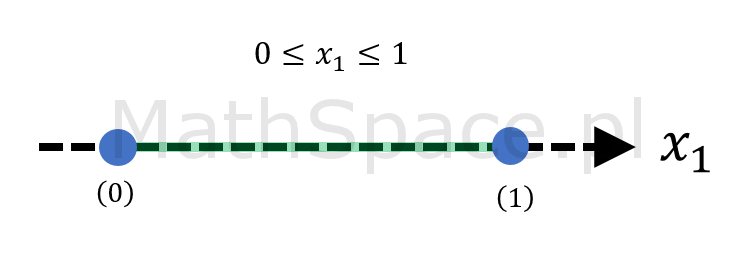
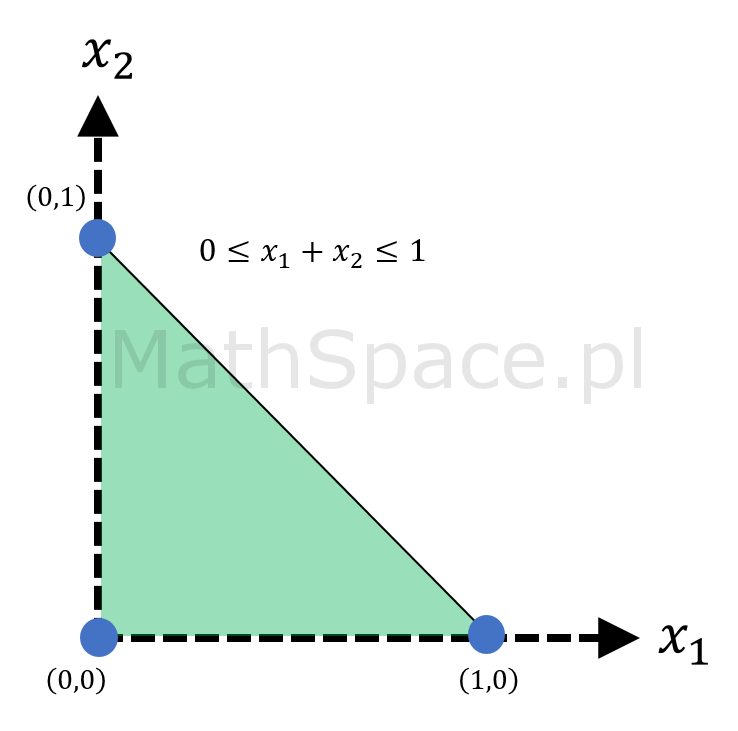
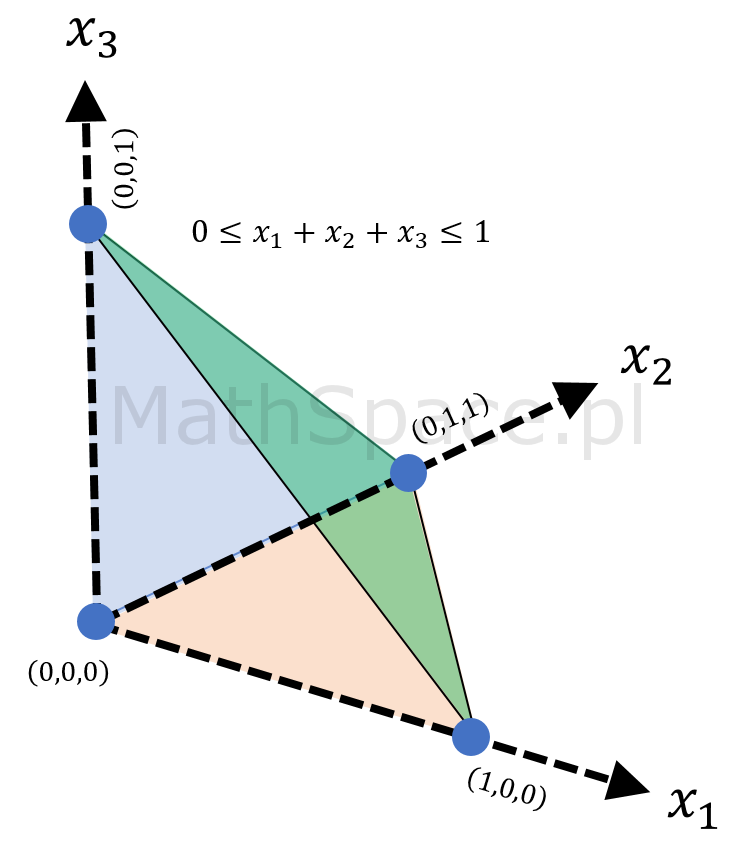
Spostrzeżenie #8: rozważany zbiór

$$\bigg\{(x_1,x_2,\ldots,x_n)\in\mathbb{R}^n~:~0\leq x_1+x_2+\ldots+x_n\leq 1\bigg\}$$

to n-sympleks.

N-sympleks i jego objętość

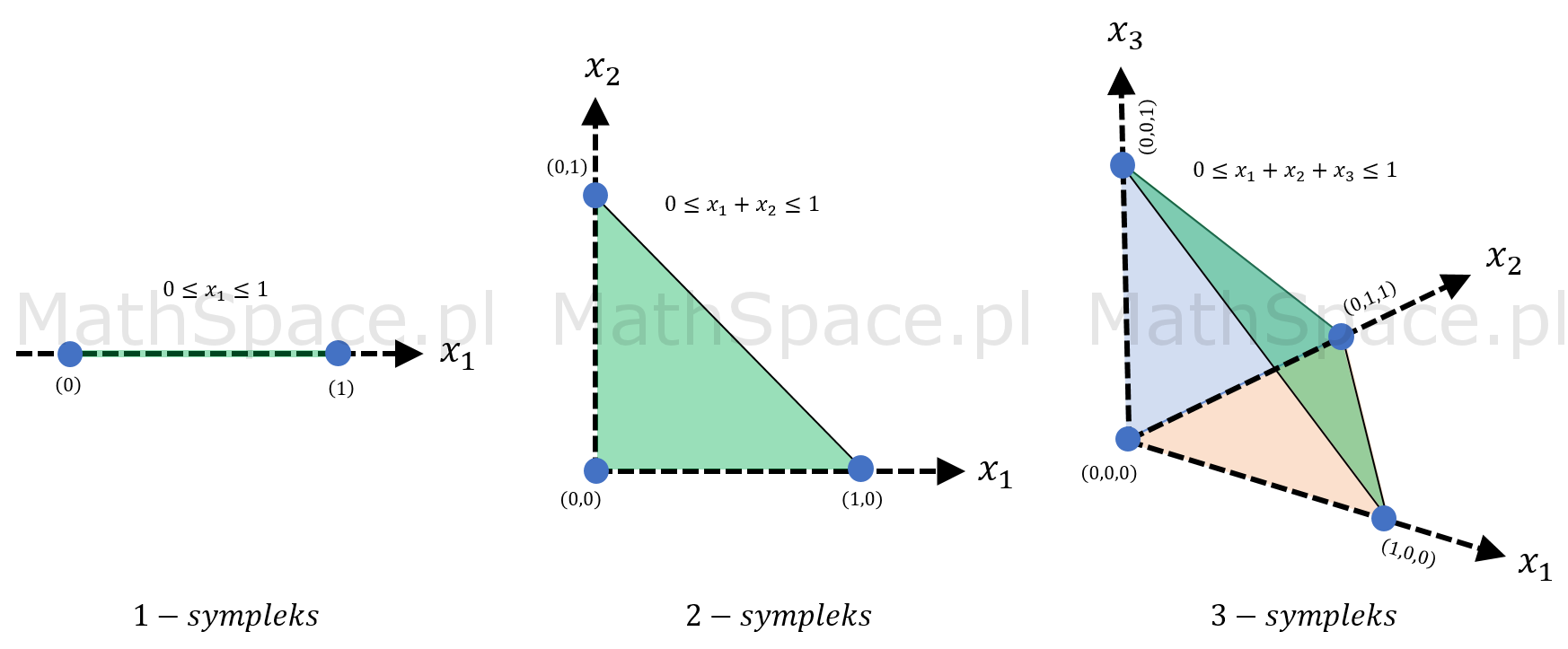
Sympleks w matematyce to uogólnienie pojęcia trójkąta na przestrzenie wielowymiarowe. Mówimy, że n-sympleks powstaje z n+1 wierzchołków, będąc obiektem osadzonym w przestrzeni k-wymiarowej. Sam sympleks to „otoczka” wypukła jego wierzchołków, jest to więc „powierzchnia”, jeśli określenie „powierzchni” ma jakikolwiek sens dla przestrzeni wielowymiarowych.

• Niech $\lambda$ będzie miarą Lebesgue’a w $\mathbb{R}^n$ – miara Lebesgue’a jest wielowymiarowym uogólnieniem pojęcia długości, pola powierzchni, objętości.
• Niech $V_n(a)$ oznacza objętość n-sympleksu przeskalowanego współczynnikiem skali podobieństwa $a$ – wtedy $V_n(1)$ to objętość „standardowego” n-sympleksu.

Możemy zapisać

$$V_n(1)=\lambda\Bigg(\Big\{0\leq x_1+x_2+\ldots+x_n\leq 1\Big\}\Bigg)$$

$$V_n(a)=\lambda\Bigg(\Big\{0\leq x_1+x_2+\ldots+x_n\leq a\Big\}\Bigg)$$

Zgodnie z założeniem, że $a$ jest współczynnikiem skali podobieństwa w przestrzeni n-wymiarowej

$$V_n(a)=a^nV_n(1)$$

$$V_n(1)=\displaystyle\int_{x_1+x_2+\ldots+x_n\leq 1}dx_1dx_2\ldots dx_n$$

$$V_n(a)=\displaystyle\int_{x_1+x_2+\ldots+x_n\leq a}dx_1dx_2\ldots dx_n$$

Zauważmy, że $x_1+x_2+\ldots+x_n\leq 1$ wtedy i tylko wtedy gdy $x_n\leq 1$ oraz $x_1+x_2+\ldots+x_{n-1}\leq 1-x_n$, więc

$$V_n(1)=\displaystyle\int_{x_n\leq 1}\Bigg(~~\underbrace{\displaystyle\int_{x_1+x_2+\ldots+x_{n-1}\leq 1-x_n}dx_1dx_2\ldots dx_{n-1}}_{V_{n-1}(1-x_n)}~~\Bigg)dx_n=$$

$$=\displaystyle\int_{x_n\leq 1}V_{n-1}(1-x_n)dx_n=\displaystyle\int_{x_n\leq 1}(1-x_n)^{n-1}V_{n-1}(1)dx_n=$$

$$=V_{n-1}(1)\displaystyle\int_{0}^1(1-x_n)^{n-1}dx_n=$$

$$=\begin{bmatrix}t=1-x_n&&t_0=1-0=1\\-dt=dx_n&&t_1=1-1=0\end{bmatrix}=$$

$$=V_{n-1}(1)\Bigg(-\displaystyle\int_{1}^0t^{n-1}dt\Bigg)=$$

$$=V_{n-1}(1)\displaystyle\int_{0}^1t^{n-1}dt=V_{n-1}(1)\Bigg[\frac{t^n}{n}\Bigg]_0^1=\frac{1}{n}V_{n-1}(1)$$

Finalnie otrzymaliśmy wzór rekurencyjny

$$V_n(1)=\frac{1}{n}V_{n-1}(1)$$

$$V_1(1)=1$$

Podstawiając kolejne wartości

$$V_2(1)=\frac{1}{2}\cdot 1=\frac{1}{1\cdot 2}$$

$$V_3(1)=\frac{1}{3}\cdot\frac{1}{1\cdot 2}=\frac{1}{1\cdot 2\cdot 3}$$

ujawnia się wzór na objętość n-sympleksu.

$$V_n(1)=\frac{1}{n!}$$

$$V_n(a)=\frac{a^n}{n!}$$

Powrót do wartości oczekiwanej $EN_1$

$$1-F_{N_1}(n)=V_n(1)=\frac{1}{n!}$$

$$EN_1=1+1+\displaystyle\sum_{n=2}^\infty\Big(1-F_{N_1}(n)\Big)=\frac{1}{0!}+\frac{1}{1!}+\displaystyle\sum_{n=2}^\infty\frac{1}{n!}$$

Ostatecznie

$$EN_1=\displaystyle\sum_{n=0}^\infty\frac{1}{n!}=e$$

Wartości oczekiwane $EN_1$, $EN_2$, $EN_3$, $EN_4$, $EN_5$

• $EN_1=e$
• $N_2=e^2-e$
• $EN_3=e^3-2e^2+\frac{e}{2}$
• $EN_4=e^4-3e^3+2e^2-\frac{e}{6}$
• $EN_5=e^5-4e^4+\frac{9e^3}{2}-\frac{4e^2}{3}+\frac{e}{24}$

Po szczegóły zapraszam do artykułu „Uniform Sum Distribution”.

Weryfikacja na bazie Monte Carlo

Eksperyment wykonany przy wykorzystaniu MathParser.org-mXparser.

/*
* Rekurencja w poszukiwaniu minimalnego 'n'
* a - liczba do przekroczenia
* s - tymczasowa suma
* k - numer losowania
*/
Function Nrec = new Function("Nrec(a, s, k) = if( s >= a, k, Nrec( a, s + [Uni], k+1 ) )");
/*
* Definicja zmiennych losowych
*/
Argument N1 = new Argument("N1 = Nrec(1,0,0)", Nrec);
Argument N2 = new Argument("N2 = Nrec(2,0,0)", Nrec);
Argument N3 = new Argument("N3 = Nrec(3,0,0)", Nrec);
Argument N4 = new Argument("N4 = Nrec(4,0,0)", Nrec);
Argument N5 = new Argument("N5 = Nrec(5,0,0)", Nrec);
/*
* Estymacja wartości oczekiwanych - 1000000 operacji
*/
Expression EN1 = new Expression("avg( i, 1, 1000000, N1 )", N1);
Expression EN2 = new Expression("avg( i, 1, 1000000, N2 )", N2);
Expression EN3 = new Expression("avg( i, 1, 1000000, N3 )", N3);
Expression EN4 = new Expression("avg( i, 1, 1000000, N4 )", N4);
Expression EN5 = new Expression("avg( i, 1, 1000000, N5 )", N5);
/*
* Teoretyczne wartości oczekiwane
*/
Expression eN1 = new Expression("e");
Expression eN2 = new Expression("e^2 - e");
Expression eN3 = new Expression("e^3 - 2*e^2 + e/2");
Expression eN4 = new Expression("e^4 - 3*e^3 + 2*e^2 - e/6");
Expression eN5 = new Expression("e^5 - 4*e^4 + 9/2 * e^3 - 4/3 * e^2 + e/24");
/*
* Obliczenie i wyswietlenie wyników
*/
mXparser.consolePrintln("EN1 - estymowane: " + EN1.getExpressionString() + " = " + EN1.calculate());
mXparser.consolePrintln("EN1 - teoretyczne: " + eN1.getExpressionString() + " = " + eN1.calculate());
mXparser.consolePrintln("------------------------------");
mXparser.consolePrintln("EN2 - estymowane: " + EN2.getExpressionString() + " = " + EN2.calculate());
mXparser.consolePrintln("EN2 - teoretyczne: " + eN2.getExpressionString() + " = " + eN2.calculate());
mXparser.consolePrintln("------------------------------");
mXparser.consolePrintln("EN3 - estymowane: " + EN3.getExpressionString() + " = " + EN3.calculate());
mXparser.consolePrintln("EN3 - teoretyczne: " + eN3.getExpressionString() + " = " + eN3.calculate());
mXparser.consolePrintln("------------------------------");
mXparser.consolePrintln("EN4 - estymowane: " + EN4.getExpressionString() + " = " + EN4.calculate());
mXparser.consolePrintln("EN4 - teoretyczne: " + eN4.getExpressionString() + " = " + eN4.calculate());
mXparser.consolePrintln("------------------------------");
mXparser.consolePrintln("EN5 - estymowane: " + EN5.getExpressionString() + " = " + EN5.calculate());
mXparser.consolePrintln("EN5 - teoretyczne: " + eN5.getExpressionString() + " = " + eN5.calculate());
mXparser.consolePrintln("------------------------------");

Wynik

[mXparser-v.4.1.1] EN1 - estymowane: avg( i, 1, 1000000, N1 ) = 2.71813
[mXparser-v.4.1.1] EN1 - teoretyczne: e = 2.718281828459045
[mXparser-v.4.1.1] ------------------------------
[mXparser-v.4.1.1] EN2 - estymowane: avg( i, 1, 1000000, N2 ) = 4.668181
[mXparser-v.4.1.1] EN2 - teoretyczne: e^2 - e = 4.670774270471606
[mXparser-v.4.1.1] ------------------------------
[mXparser-v.4.1.1] EN3 - estymowane: avg( i, 1, 1000000, N3 ) = 6.666433
[mXparser-v.4.1.1] EN3 - teoretyczne: e^3 - 2*e^2 + e/2 = 6.666565639555883
[mXparser-v.4.1.1] ------------------------------
[mXparser-v.4.1.1] EN4 - estymowane: avg( i, 1, 1000000, N4 ) = 8.664254
[mXparser-v.4.1.1] EN4 - teoretyczne: e^4 - 3*e^3 + 2*e^2 - e/6 = 8.66660449003271
[mXparser-v.4.1.1] ------------------------------
[mXparser-v.4.1.1] EN5 - estymowane: avg( i, 1, 1000000, N5 ) = 10.667831
[mXparser-v.4.1.1] EN5 - teoretyczne: e^5 - 4*e^4 + 9/2 * e^3 - 4/3 * e^2 + e/24 = 10.66666206862245

Wszystko się zgadza! Niesamowite powiązanie!

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa