W części #17 cyklu „Ocena jakości klasyfikacji” wydobędę kolejne informacje z krzywej Captured Response, która, na pierwszy rzut oka, prezentuje wyłącznie TPR (True-Positive-Rate). Kontynuuję zatem serię „Tips & Tricks na krzywych”.
Prawdopodobieństwo skumulowane (PPV, PRECISION) na bazie TPR czyli Captured Response
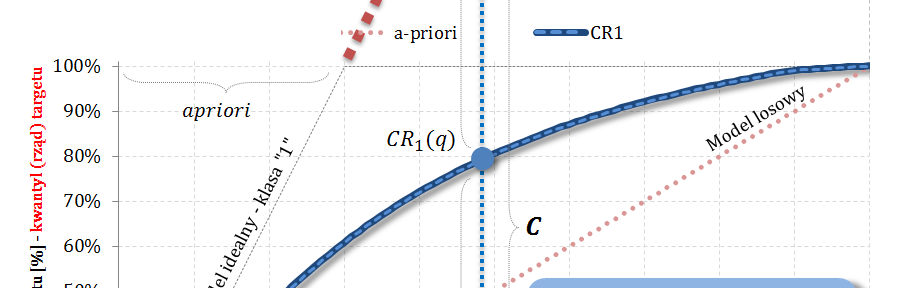
Dla modelu idealnego krzywa Captured Response ma postać
$$Capt.Resp(q)=\begin{cases}\frac{q}{apriori}&\text{dla}\quad q\leq apriori\\1&\text{dla}\quad q>apriori\end{cases}$$
$q$ – kwantyl (rząd) bazy (malejąco względem oceny modelem)
Rozważając „przedłużenie pierwszej części” definicji na cały odcinek $[0;1]$ otrzymujemy „skalę”, na bazie której łatwo wyznaczyć PPV (Positive Predicted Value) oraz FDR (False Discovery Rate).
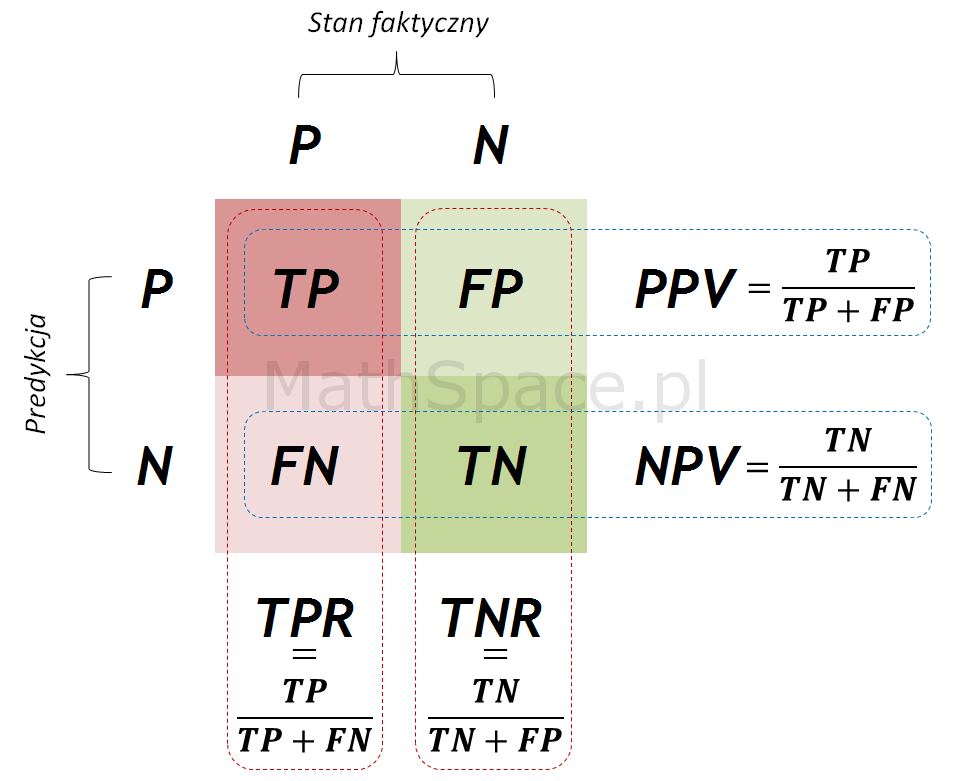
$$PPV=\frac{TP}{TP+FP}$$
$$FDR=\frac{FP}{TP+FP}=1-PPV$$
Zależności
$$PPV(q)=\frac{apriori\times TPR(q)}{q}$$
$$FDR(q)=1-PPV(q)=1-\frac{apriori\times TPR(q)}{q}$$
$q$ – cut-off jako kwantyl (rząd) bazy (malejąco względem oceny modelem)
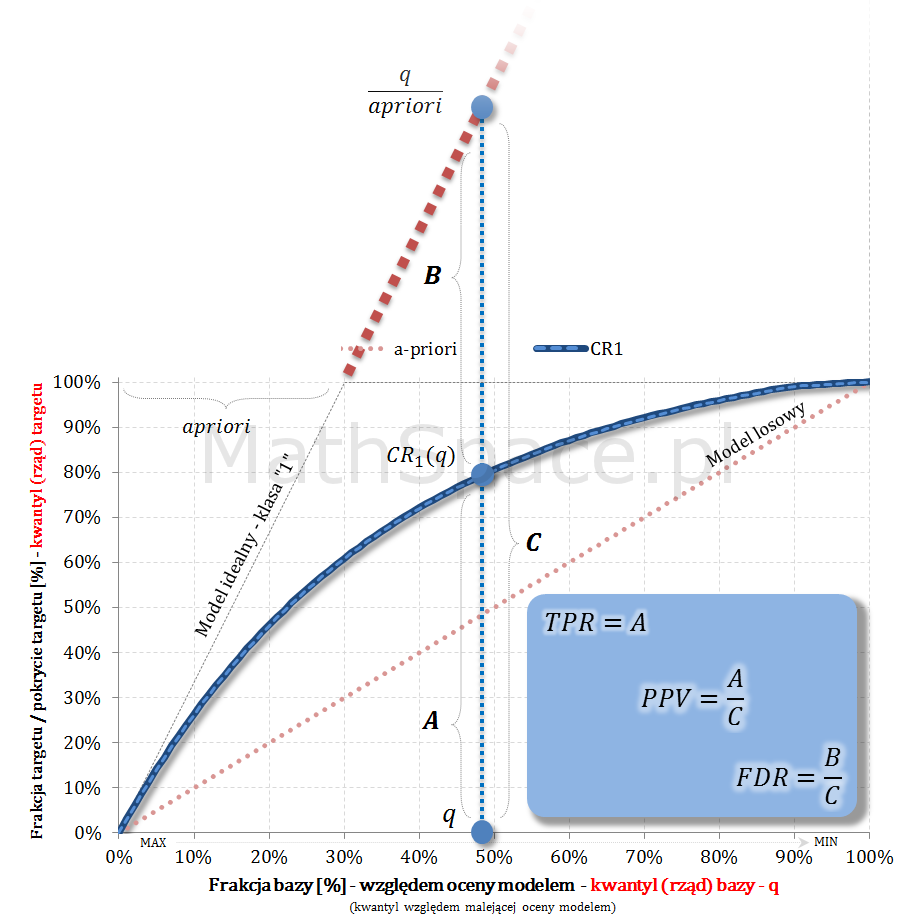
Dowód: zaczynamy od oznaczeń
- $N=N_1+N_0$ – liczba obiektów w populacji: total, z klasy pozytywnej „1”, z klasy negatywnej „0”;
- $q$ – cut-off (jako kwantyl – a dokładnie jego rząd – względem malejącej oceny modelem);
- $[0,q]$ – klasyfikacja pozytywna;
- $(q,1]$ – klasyfikacja negatywna;
- $n_1$ – true positive;
- $n_0$ – false positive;
- $n=n_1+n_0$
- $q=\frac{n}{N}$
- $apriori=\frac{N_1}{N}$
$$PPV(q)=\frac{n_1}{n}$$
$$A=TPR(q)=\frac{n_1}{N_1}$$
$$C=\frac{q}{apriori}=\frac{n}{N}\times\frac{N}{N_1}=\frac{n}{N_1}$$
$$\frac{A}{C}=\frac{n_1}{N_1}\times\frac{N_1}{n}=\frac{n_1}{n}$$
$$\frac{A}{C}=PPV(q)$$
$$\frac{A}{C}=TPR(q)\times\frac{apriori}{q}=\frac{apriori\times TPR(q)}{q}$$
$$PPV(q)=\frac{apriori\times TPR(q)}{q}$$
cbdo. 🙂
Wydaje mi się, że analogicznie można wyznaczyć NPV – tylko tu analizując: klasyfikację do klasy negatywnej, krzywą Captured Response dla klasy „0” (TNR) oraz „przedłużenie” modelu idealnego dla klasy „0” – sprawdzimy 🙂
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa
