Do napisania 16 części cyklu „Ocena jakości klasyfikacji” zainspirował mnie Kolega i dawny współpracownik! Michał – dzięki za „hint” 🙂 Dziś wskażę pewien sympatyczny punkt przecięcia, którego znajomość jest przydatna, a już z pewnością można „zaszpanować” 🙂 Wpis stanowi zdecydowane wzbogacenie serii „Tips & Tricks na krzywych”.
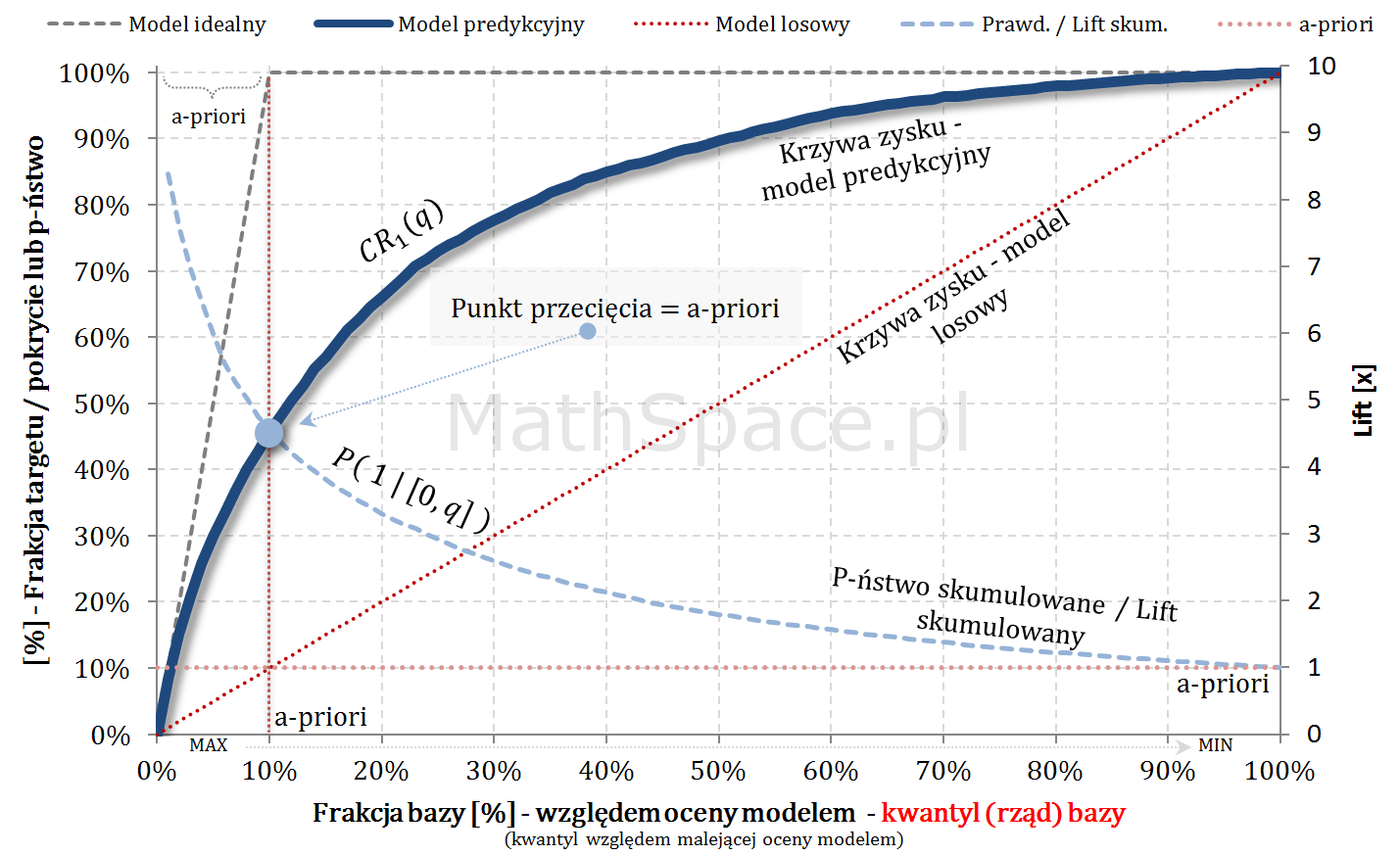
Krzywe Captured Response (TPR) i prawdopodobieństwo skumulowane (PPV, Precision) przecinają się w punkcie a-priori 🙂
Dowód: zaczynamy od oznaczeń:
- $N=N_1+N_0$ – liczba obiektów w populacji: total, z klasy pozytywnej „1”, z klasy negatywnej „0”;
- $q$ – cut-off (jako kwantyl – a dokładnie jego rząd – względem malejącej oceny modelem);
- $[0,q]$ – klasyfikacja pozytywna;
- $(q,1]$ – klasyfikacja negatywna;
- $n_1(q)$ – true positive;
- $n_0(q)$ – false positive;
- $n(q)=n_1(q)+n_0(q)=q\cdot N$
Wtedy
$$TPR(q)=CR_1(q)=\frac{n_1(q)}{N_1}=\frac{n_1(q)}{apriori\times N}$$
$$PPV(q)=P\big(~1~|~[0,q]~\big)=\frac{n_1(q)}{n(q)}=\frac{n_1(q)}{qN}$$
Porównując
$$PPV(q)=TPR(q)$$
$$\frac{n_1(q)}{qN}=\frac{n_1(q)}{apriori\times N}$$
Zakładając, że $n_1(q)\neq 0$
$$q=apriori$$
cbdo 🙂
Do czego „sympatyczny” punkt przecięcia może się przydać?
Znajomość punktu przecięcia może się przydać do weryfikacji poprawności analizowanych wykresów i ich spójności z założeniami. Przykładowo – jeśli analityk na jednym wykresie naniesie Captured Response wraz z modelem idealnym, następnie do wykresu doda p-ństwo skumulowane (czyli PPV), i jeśli te krzywe przetną się w innym punkcie niż „aprirori”, to gdzieś mamy błąd! Być może prezentowane wykresy przedstawiają różne modele?
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa
