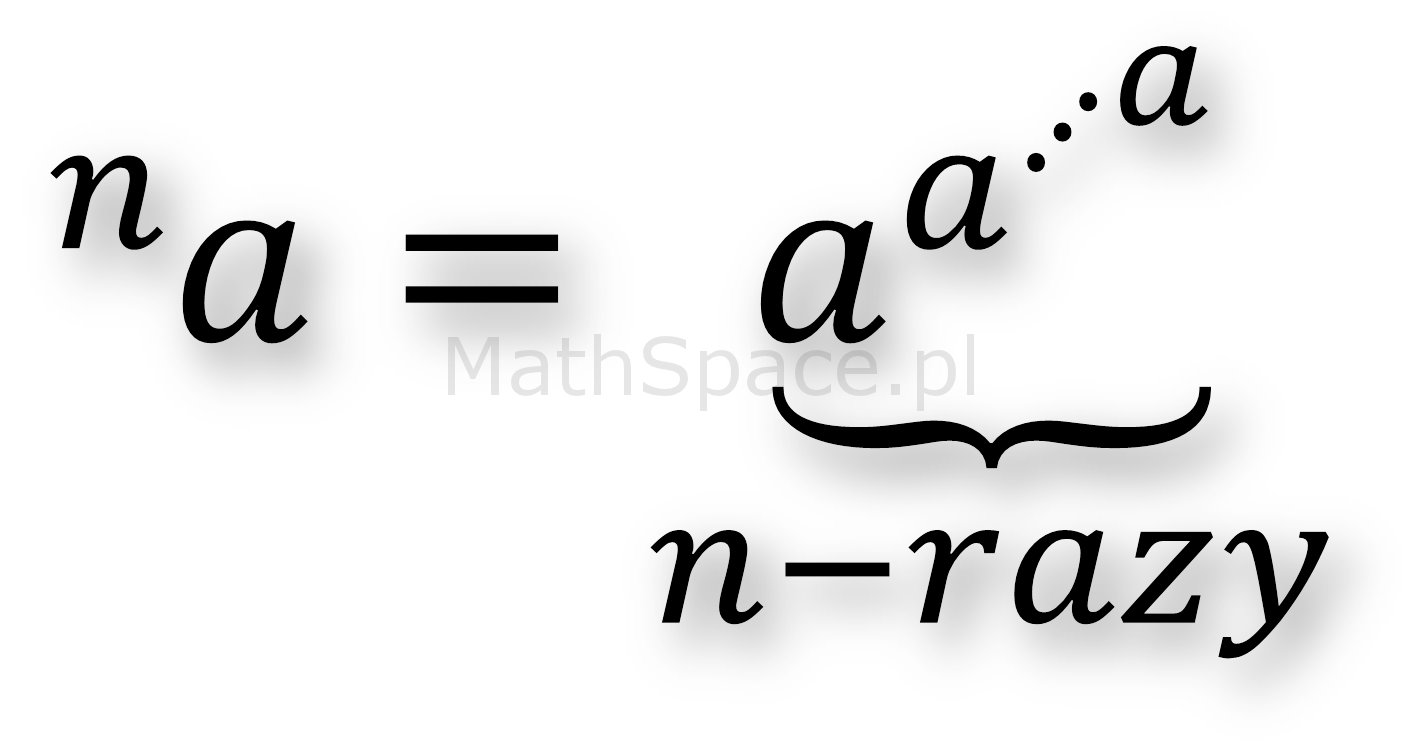
Tetracja (wieża wykładnicza, super-potęgowanie, iterowane potęgowanie, 4 hiper-operator)
Tetracja to działanie dwuargumentowe definiowane jako wielokrotne potęgowanie elementu przez siebie.
Definicja: dla dowolnej liczby rzeczywistej $a>0$ i nieujemnej liczby całkowitej $n\geq 0$ tetrację $n$ liczby $a$ definiujemy jako:
$${^{n}a}=\begin{cases}1&\text{dla}\quad n=0\\a&\text{dla}\quad n=1\\ \underbrace{a^{a^{\cdots^{a}}}}_{n}&\text{dla}\quad n>1\end{cases}$$
Przykłady
$${^{3}2}=2^{2^2}=2^{(2^2)}=2^4=16$$
$${^{4}2}=2^{2^{2^2}}=2^{(2^{(2^2)})}=2^{(2^{4})}=2^{16}=65536$$
$${^{3}3}=3^{3^3}=3^{(3^3)}=3^{27}=7625597484987$$
$${^{4}3}=3^{3^{3^3}}=3^{(3^{(3^3)})}=3^{(3^{27})}=3^{7625597484987}=\ldots$$ liczba składająca się z $$3638334640025$$ cyfr 🙂
Tetrację można wykorzystać do zapisu naprawdę dużych liczb, co dobrze obrazuje przykład ${^{4}3}$. Tetrację wygodnie jest również definiować w postaci rekurencyjnej.
Definicja rekurencyjna: dla dowolnej liczby rzeczywistej $a>0$ i nieujemnej liczby całkowitej $n\geq 0$ tetrację $n$ liczby $a$ definiujemy jako:
$${^{n}a}=\begin{cases}1&\text{dla}\quad n=0\\a^{{^{n-1}a}}&\text{dla}\quad n\geq 1\end{cases}$$
Funkcja $f(x)=x^x$ i związek tetracji z liczbą $e$
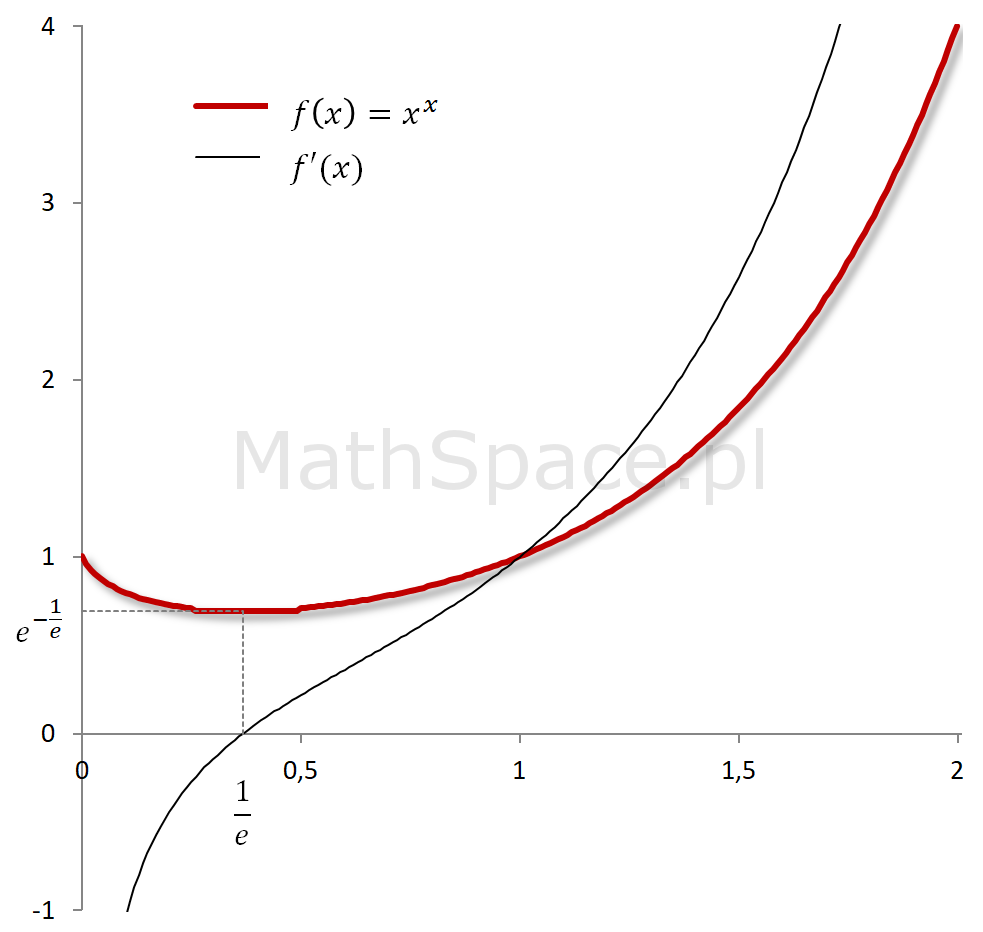
$f(x)=x^x$ to podstawowy przykład funkcji na bazie tetracji.
Własności $f(x)=x^x$
- $f(x)=x^x$ jest określona na dodatnich liczbach rzeczywistych
- $0^0$ jest symbolem nieokreślonym, ale $x^x\to 1$ gdy $x\to 0^+$
- $f(x)=x^x$ posiada minimum $e^{-\frac{1}{e}}$ w punkcie $x=\frac{1}{e}$
- $f(x)=x^x$ maleje w przedziale $x\in(0, \frac{1}{e})$, rośnie w przedziale $x\in(\frac{1}{e},+\infty)$
- $f^\prime(x)=x^x\big(\ln x+1\big)$
Pochodna $f(x)=x^x$
Aby policzyć pochodną $x^x$ wystarczy zastosować drobny trick na bazie własności logarytmu.
$$f(x)=x^x$$
$x>0$ oraz $f(x)>0$
$$\ln f(x)=\ln x^x=x\ln x$$
$$\Big(\ln f(x)\Big)^\prime=\Big(x\ln x\Big)^\prime$$
$$\frac{1}{f(x)}f^\prime(x)=x^\prime\ln x + x\Big(\ln x\Big)^\prime=\ln x + 1$$
$$f^\prime(x)=(x^x)^\prime$$
$$f^\prime(x)=f(x)\Big(\ln x + 1\Big)=x^x\Big(\ln x + 1\Big)$$
Bazując na rekurencyjnej definicji tetracji, korzystając z powyższego tricku, można wyznaczyć ogólną rekurencyjną formułę na pochodną tetracji $n$ liczby $x$. Mając pochodną z łatwością wykazujemy większość podanych własności.
Nieskończona wieża wykładnicza i jeszcze silniejszy związek tetracji z liczbą $e$
$${\Huge x^{x^{x^{x^{x^{\cdots}}}}}=?}$$
Problem zbieżności ciągu tetracji został rozwiązany już w XVIII wieku, a dokonał tego Leonhard Euler 🙂 Rozważmy granicę
$$\lim_{n\to\infty}{^{n}x}$$
zadając pytanie „dla jakich $x>0$ istnieje powyższa granica?”
Na potrzeby rozważań załóżmy, że taka granica istnieje i wynosi
$$\lim_{n\to\infty}{^{n}x}=y$$
Bazując na rekurencyjnej definicji tetracji otrzymujemy
$$y=\lim_{n\to\infty}{^{n}x}=\lim_{n\to\infty}x^{^{n-1}x}=$$
$$=x^{\lim_{n\to\infty}{^{n-1}x}}=x^y$$
Zatem, warunkiem koniecznym dla zbieżności ciągu tetracji jest
$$y=x^y$$
gdzie
$$\lim_{n\to\infty}{^{n}x}=y$$
Przekształcając $y=x^y$
$$y^{\frac{1}{y}}=(x^y)^{\frac{1}{y}}$$
otrzymujemy
$$x=y^\frac{1}{y}$$
Uwaga: nie jest to warunek dostateczny!
Twierdzenie Eulera o zbieżności ciągu tetracji: $y=\lim_{n\to\infty}{^{n}x}$ istnieje i jest skończona wyłącznie jeśli $x\in\Big[e^{-e},e^\frac{1}{e}\Big]$. Zachodzi wtedy
$$y\in\Big[\frac{1}{e},e\Big]$$
dla
$$x\in\Big[e^{-e},e^\frac{1}{e}\Big]$$
Dowód powyższego twierdzenia wykracza poza objętość tego artukułu, zainteresowanych zapraszam do publikacji R. Arthur Knoebel , Exponentials Reiterated.

Na koniec niesamowita estetyka, która ujawnia się w nieskończonej wieży wykładniczej
W przedziale $y\in\Big[\frac{1}{e},e\Big]$ leżą tylko dwie liczby całkowite: 1 i 2.
$y=1$ to $x=1$
$y=2$ to $x=2^\frac{1}{2}=\sqrt{2}$
Piękne – nieskończona tetracja $\sqrt{2}$ daje w wyniku $2$ 🙂

Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
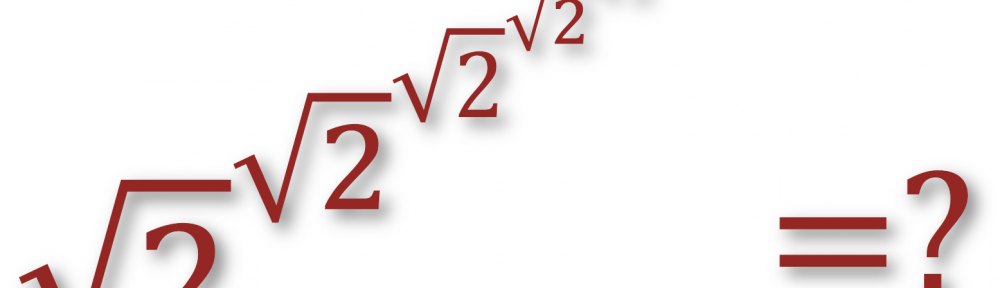

Jak zawsze świetny artykuł. Czy tetracja ma jakieś zastosowanie w data science?
Dzięki! W kwestii zastosowań w data science – raczej nie. Jedyny związek jaki widzę na szybko, to prawo iterowanego logarytmu. Iterowany logarytm i super-logarytm są powiązane, a super-logarytm to odwrotność tetracji.
No właśnie… Przykład nr.1, jeśli rozwiążemy równanie:
x^(x^(x^(x^(x^….)=2
zauważając, że w wartość w wykładniku jest taka sama jak całe wyrażenie, otrzymamy:
x^2=2
więc x=sqrt(2)
No więc faktycznie tak jest co ładnie obrazuje animacja w poście powyżej.
A teraz przykład nr.2, rozwiążmy równanie:
x^(x^(x^(x^(x^….)=4
Robiąc ten sam trik otrzymujemy:
x^4 = 4
x=4^(1/4)
no ale przecież 4^(1/4) to pierwiastek kwadratowy z 2, jak więc dla tej samej wartości x można otrzymać raz 2 a raz 4? W zasadzie sprawdziliśmy przed chwilą że nieskończona tetracja pierwiastka z 2 równa jest 2, więc co jest nie tak w przykładzie nr. 2? 😉
Nieskończona tetracja jest zbieżna jedynie dla x >= e^(-e) oraz x <= e^(1/e), wartość do której zbiega jest z przedziału (1/e, e) - jest to tw. Eulera, zatem przypadek zbieżności do 4 wykluczamy na bazie tw. Eulera.