Część #18 cyklu „Ocena jakości klasyfikacji” to pogłębienie interpretacji krzywej Liftu Skumulowanego – mam wrażenie, że to już ostatni wpis z serii „Tips & Tricks na krzywych”.
TPR (Captured Response) i FNR na bazie Liftu Skumulowanego
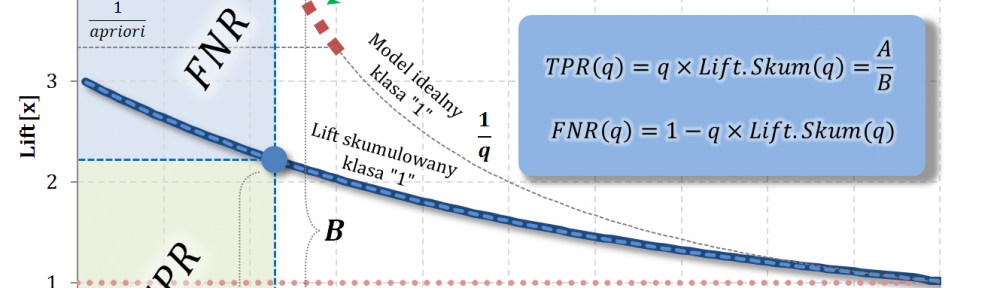
Dla modelu idealnego krzywa liftu skumulowanego przyjmuje następującą postać:
$$Lift.Skum(q)=\begin{cases}\frac{1}{apriori}&\text{dla}\quad q\leq apriori\\\frac{1}{q}&\text{dla}\quad q>apriori\end{cases}$$
$q$ – kwantyl (rząd) bazy (malejąco względem oceny modelem)
Stosując technikę „przedłużania modelu idealnego”, analogicznie do zastosowanej w części #17 „PPV i FDR na bazie TPR”, tworzymy „skalę” umożliwiającą wyznaczenie TPR (True-Positive Rate) oraz FNR (False-Negative Rate).
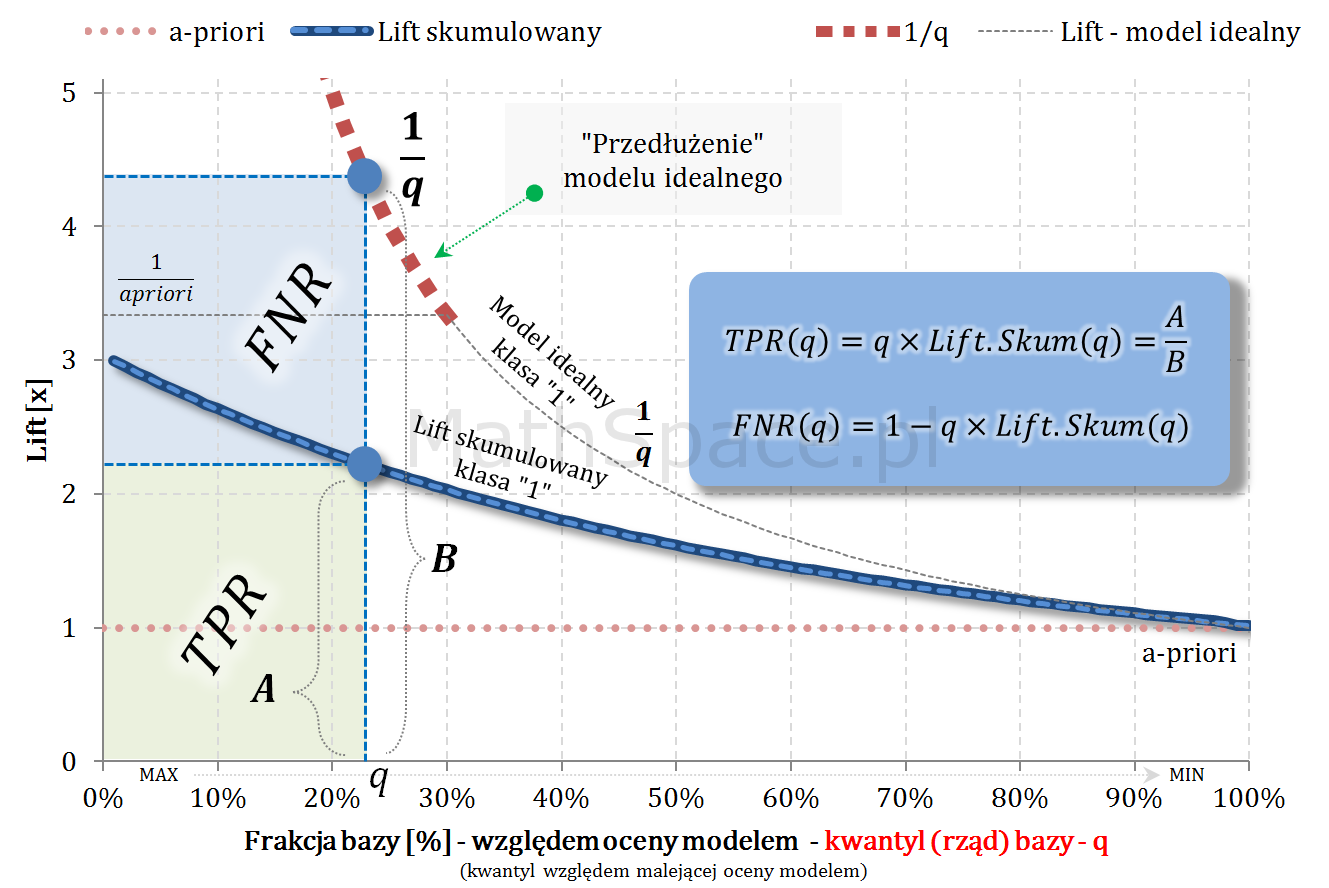
Zależności
$$TPR(q)=q\times Lift.Skum(q)=\frac{A}{B}$$
$$A=Lift.Skum(q)$$
$$B=\frac{1}{q}$$
Dowód: w części #11 „Captured Response vs Lift” pokazałem, że
$$\frac{CR(q)}{q}=Lift.Skum(q)$$
ale $CR(q)$ to to samo co $TPR(q)$ – różni się tylko nazwą 🙂
Nieco inny dowód podałem również w części #17 „PPV i FDR na bazie TPR”
$$PPV(q)=\frac{apriori\times TPR(q)}{q}$$
trochę przekształcając otrzymujemy
$$\frac{PPV(q)}{apriori}\times q=TPR(q)$$
Dalej wystarczy zauważyć, że
$$\frac{PPV(q)}{apriori}=Lift.Skum(q)$$
cbdo. 🙂
I ponownie – wydaje mi się, że analogicznie można naszkicować TNR oraz FPR – tylko tu analizując: klasyfikację do klasy negatywnej, krzywą Liftu Skumulowanego dla klasy „0” oraz „przedłużenie” modelu idealnego dla klasy „0” – wymaga sprawdzenia 🙂
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.