W części 4 cyklu „ocena jakości klasyfikacji” opisałem podstawowe statystyki w wariancie nieskumulowanym służące inspekcji modelu predykcyjnego. Nieskumulowane prawdopodobieństwo i nieskumulowany lift, choć bardzo przydatne na etapie budowy modelu (praca analityka), sprawdzają się nieco gorzej w kontaktach analityk – odbiorca biznesowy. Odbiorcę biznesowego zazwyczaj interesują informacje takie jak „do jakiej części zainteresowanych produktem dotrę?” lub „o ile skuteczniejsze jest targetowanie na bazie modelu?” (tu uwaga dla bardziej zaawansowanego czytelnika – celowo pomijam kwestie wpływu inkrementalnego – tzw. uplift będzie tematem przyszłych wpisów).
Założenia – przypomnienie
Podobnie do poprzednich część cyklu załóżmy, że rozważamy przypadek klasyfikacji binarnej (dwie klasy: „Pozytywna – 1” nazywana targetem oraz „Negatywna – 0”). Załóżmy ponadto, że dysponujemy modelem predykcyjnym $p$ zwracającym prawdopodobieństwo $p(1|x)$ przynależności obserwacji $x$ do klasy „Pozytywnej – 1” (inaczej „P od 1 pod warunkiem, że x”). I jeszcze ostatnie założenie, wyłącznie dla uproszczenia wizualizacji – dotyczy rozmiaru klasy pozytywnej – tym razem ustalmy, że jest to 5%, inaczej, że prawdopodobieństwo a-priori P(1)=0.05.
Skumulowane prawdopodobieństwo i skumulowany lift – czyli o ile skuteczniejsze jest targetowanie na bazie modelu?
Pojęcie liftu dobrze jest utożsamiać z krotnością rozumianą jako „o ile razy częściej zaobserwuję target w grupie wybranej modelem w stosunku do wyboru losowego”. Interpretacja „krotnościowa” ma zastosowaniu zarówno do liftu skumulowanego i nieskumulowanego. Lift nieskumulowany powstaje na bazie obserwacji targetu w określonym przedziale estymowanego prawdopodobieństwa (np. pojedynczy centyl, pojedynczy decyl), natomiast lift skumulowany odnosi się do targetu analizowanego we wszystkich przedziałach estymowanego prawdopodobieństwa, które leżą „na lewo” od ustalonego puntu (czyli np. 20 pierwszych centyli, 2 pierwsze decyle).
Ideę liftu najlepiej obrazuje wykres prawdopodobieństwa i liftu:
- Oś pozioma – frakcja bazy względem oceny modelem – czyli baza posortowana względem estymowanego prawdopodobieństwa (czasami mówimy również względem score) w porządku od wartości największej do najmniejszej.
- Lewa oś pionowa – prawdopodobieństwo / target rate – częstość obserwacji targetu w określonym przedziale / przedziałach.
- Prawa oś pionowa – lift – normalizacja do średniego target rate (dzielenie przez a-priori).
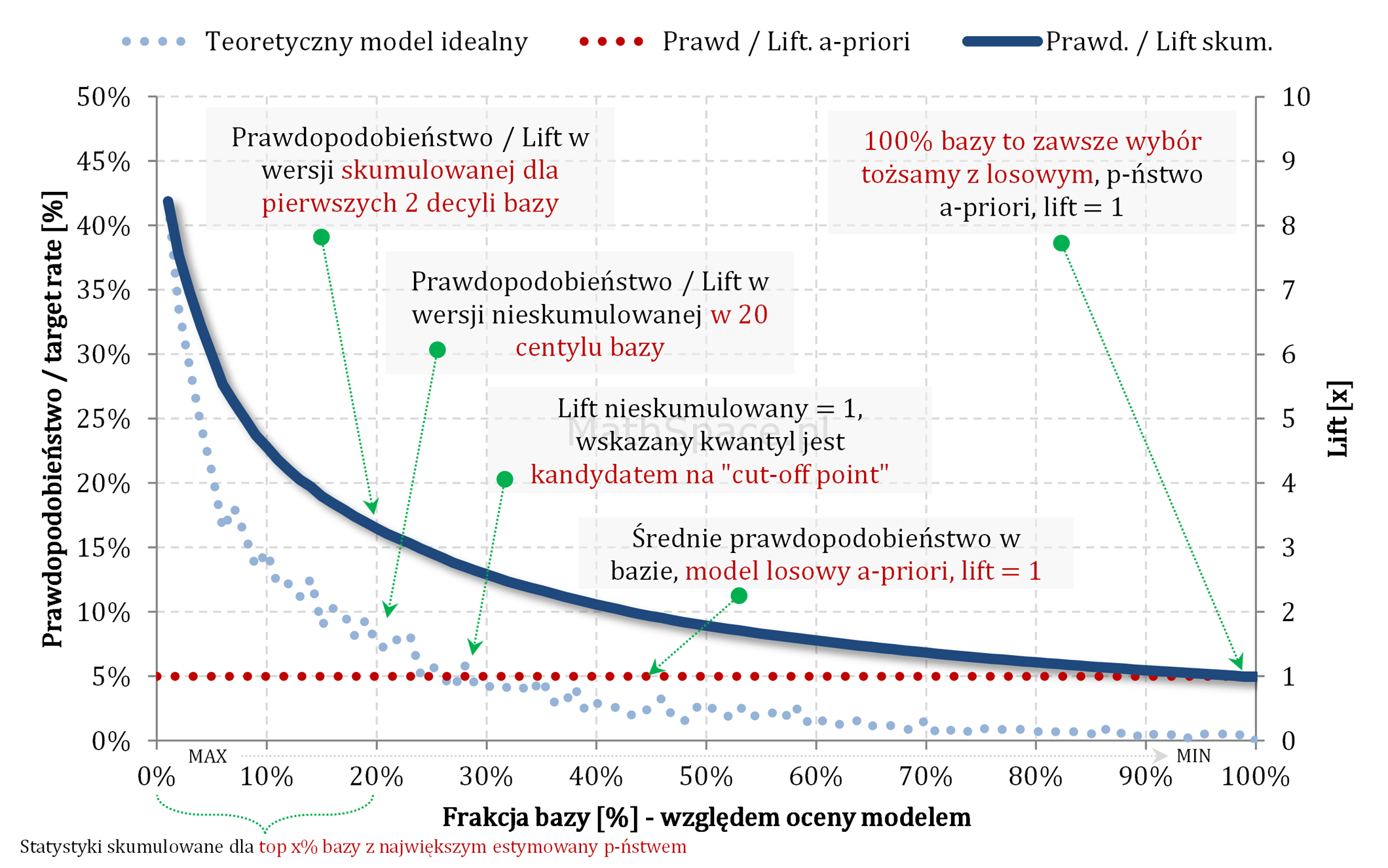
I tak – dla powyższego przykładu – mamy lift ponad 3 przy decyzji, że „cut-off point” umieszczamy dokładnie w 20 centylu. Ale zaraz – przecież na 10 centylu mamy lift ponad 4 – czyli lepiej? …
Krzywa zysku aka Gain Curve lub Captured Response – czyli do jakiej części zainteresowanych produktem dotrę?
… Rozwiązaniem powyższego dylematu jest analiza krzywej zysku. Krzywa zysku łączy w sobie ideę liftu wraz z „zasięgiem„ grupy. Przykładowo: z bazy 100 tys. klientów, w której 5 tys. zainteresowanych jest produktem, do kampanii wybrano 10 tys. Po realizacji komunikacji okazało się, że spośród 10 tys. zakupu dokonało 3 tys. klientów. I dochodzimy łatwo do definicji zasięgu jako pokrycia 3 tys. z 5 tys, czyli dotarcie do targetu na poziomie 3/5 = 60%.
Ideę zasięgu bardzo dobrze obrazuje wykres krzywej zysku:
- Oś pozioma – tak jak dla liftu – frakcja bazy względem oceny modelem.
- Oś pionowa – zasięg
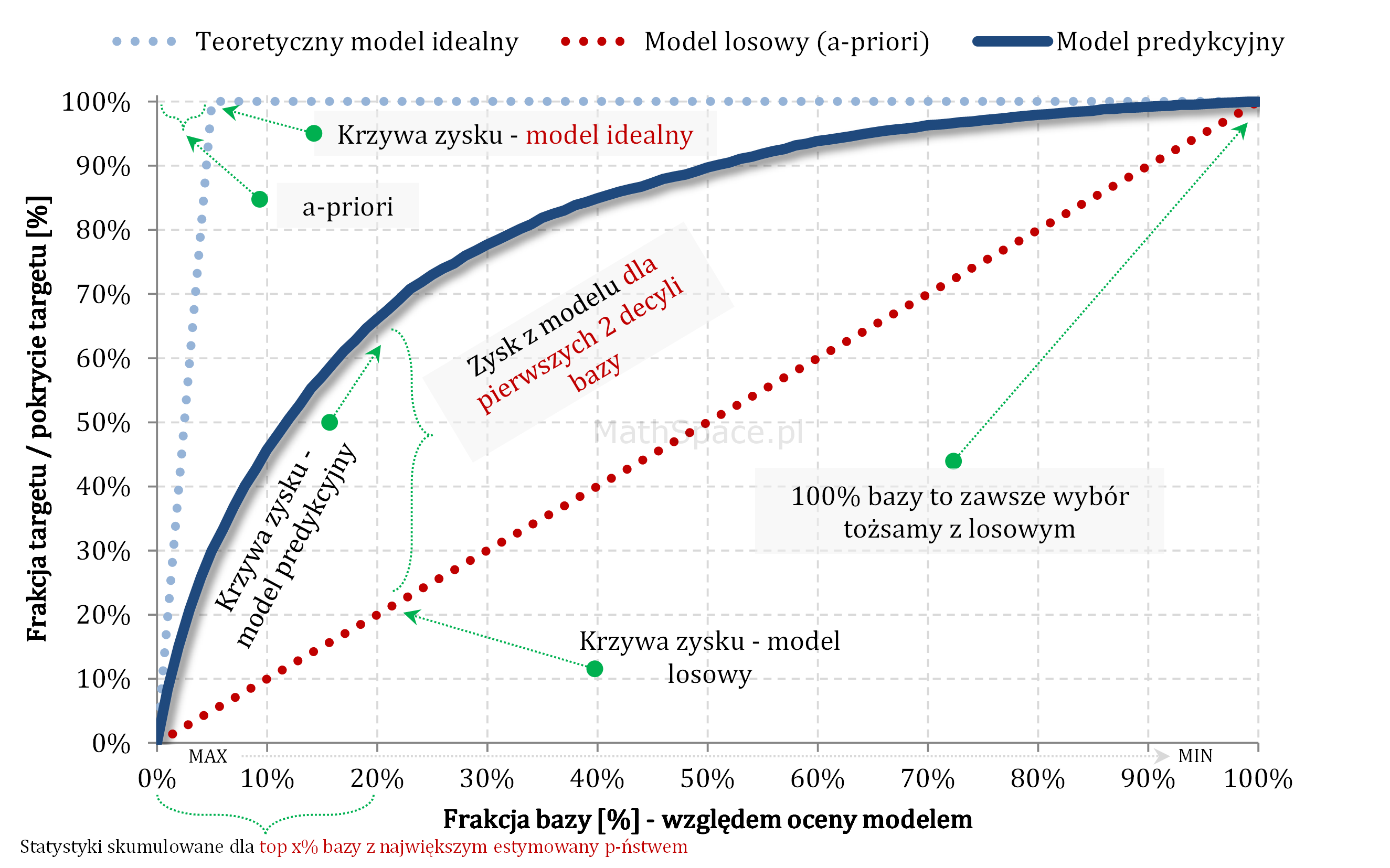
Analizując powyższy przykład – zasięg na 10% to około 45%, na 20% to już około 65% – czyli „chyba warto się pochylić” 🙂 … cdn …
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
