W pierwszych trzech częściach „Zabaw z rekurencją” skupialiśmy się na rekurencji bezpośredniej, tzn. na sytuacji, kiedy w ciele funkcji dochodzi do wywołania „siebie samej”. Przebieg rekurencji bezpośredniej jest dość oczywisty, struktura wywołania, argumenty, jak też warunek stopu, są takie same dla wszystkich odwołań.
Rekurencja pośrednia
O rekurencji pośredniej mówimy w sytuacji „łańcucha wywołań”. Przykładowo funkcja f(.) wywołuje funkcję g(.), następnie funkcja g(.) wywołuje f(.), zatem ponowne wywołanie funkcji f(.) realizowane jest bezpośrednio przez funkcję g(.), jednak pośrednio przez f(.), gdyż to f(.) wywołała g(.).
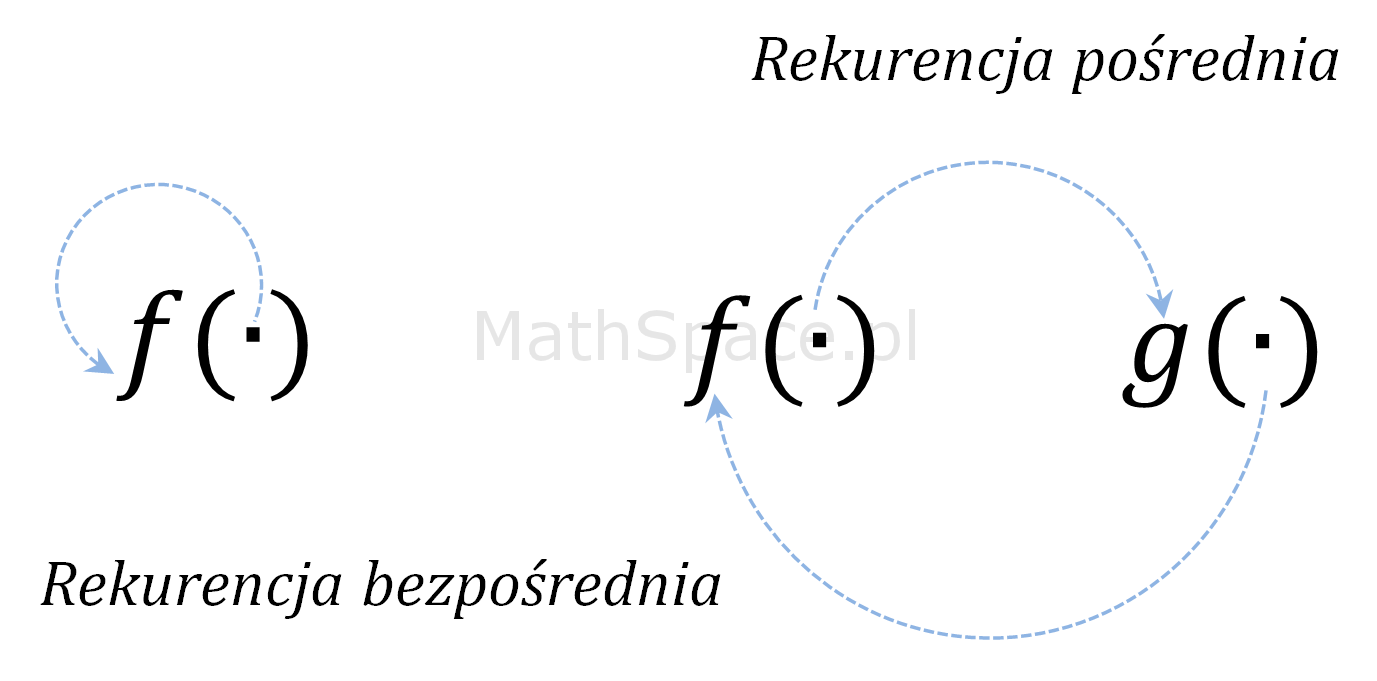
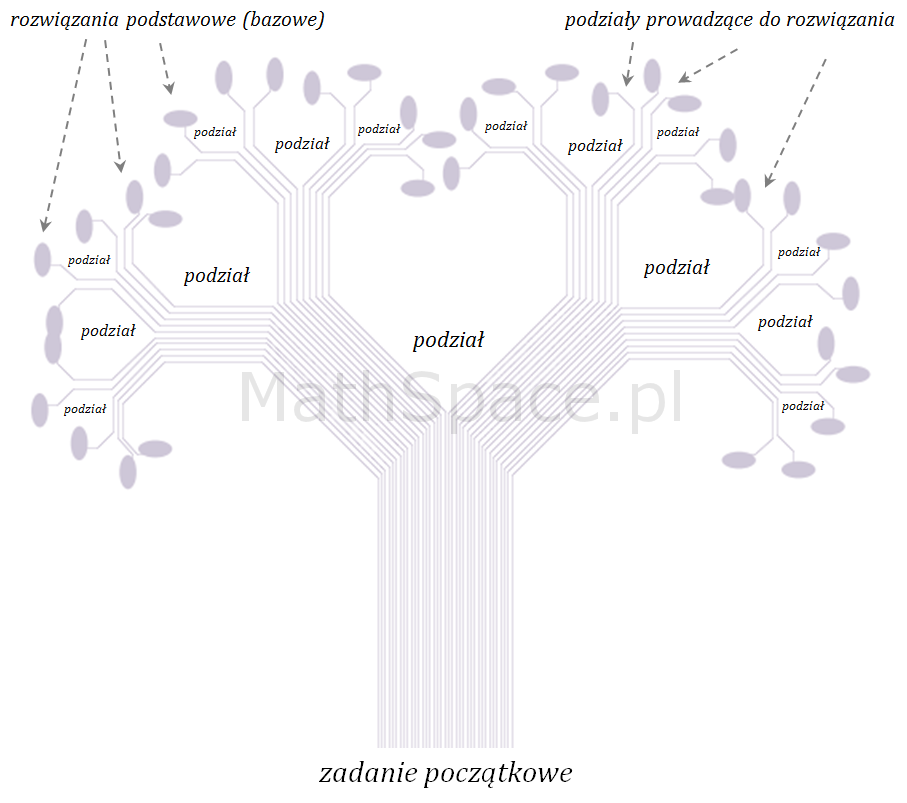
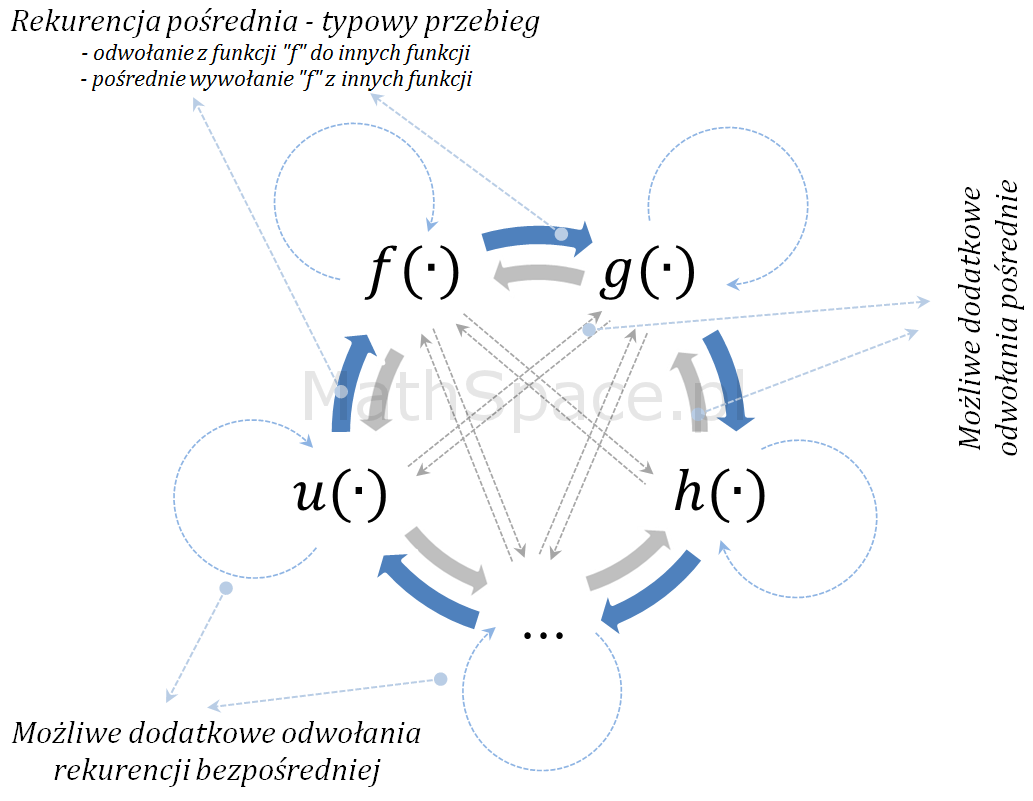
Długość łańcucha nie musi być ograniczona, w rzeczywistości wywołania pośrednie mogą mieć nietrywialną strukturę, mogą „cofać się” do poprzednich elementów, „iść na skróty”, „rozdzielać się”, a w szczególności może dochodzić do wariantów mieszanych – tzn. wywołań bezpośrednich i pośrednich (różnego typu) w ramach jednej procedury. Dobrze to obrazuje poniższy schemat.
Aproksymacja funkcji sin(x) oraz cos(x) przy wykorzystaniu połączenia rekurencji bezpośredniej i rekurencji pośredniej
Przypomnijmy podstawowe tożsamości trygonometryczne dla wielokrotności kątów.
$$\sin(2x)=2\sin(x)\cos(x)$$
$$\cos(2x)=\cos^2(x)-\sin^2(x)$$
Równoważnie powyższe można zapisać jako
$$\sin(x)=2\sin\big(\frac{x}{2}\big)\cos\big(\frac{x}{2}\big)$$
$$\cos(x)=\cos^2\big(\frac{x}{2}\big)-\sin^2\big(\frac{x}{2}\big)$$
Zwróćmy uwagę, że znając rozwiązanie dla argumentu mniejszego $\frac{x}{2}$ możemy podać rozwiązanie dla $x$ – zatem tożsamości trygonometryczne są w istocie rekurencją z odwołaniami bezpośrednimi i pośrednimi! Funkcję $\sin(x)$ w otoczeniu $0$ można przybliżyć przez $x$, natomiast funkcję $\cos(x)$ przez stałą wartość $1$. Im mniejsze otoczenie $0$ wybierzemy tym lepsza aproksymacja w zadanym przedziale, a w konsekwencji mniejszy błąd oszacowania w całości. Przyjęte wartości w otoczeniu $0$ dają również pewny warunek stopu! Mamy więc wszystko co niezbędne do zastosowania strategii rekurencyjnej w aproksymacji.
Ustalmy stałą $a>0$ (reprezentującą otoczenie $0$), następnie definiujemy dwie funkcje rekurencyjne
$$\text{s}(x)=\begin{cases}x&\text{dla}\quad |x|<a\\2\text{s}\big(\frac{x}{2}\big)\text{c}\big(\frac{x}{2}\big)&\text{dla}\quad |x|\geq a\end{cases}$$
$$\text{c}(x)=\begin{cases}1&\text{dla}\quad |x|<a\\\text{c}^2\big(\frac{x}{2}\big)-\text{s}^2\big(\frac{x}{2}\big)&\text{dla}\quad |x|\geq a\end{cases}$$
Podkreślmy ponownie, że funkcja $\text{s}(x)$ wywołuje siebie bezpośrednio oraz wskazuje na funkcję $\text{c}(x)$, która, oprócz bezpośredniego wywołania siebie samej, wskazuje ponownie na $\text{s}(x)$. Jest to zatem ciekawa kombinacja rekurencji bezpośredniej z rekurencją pośrednią. Zapiszmy to w MathParser.org-mXparser.
/* Definicja funkcji rekurencyjncyh */ Constant a = new Constant("a = 0.1"); Function s = new Function("s(x) =&amp;nbsp; if( abs(x) &amp;lt; a, x, 2*s(x/2)*c(x/2) )", a); Function c = new Function("c(x) =&amp;nbsp; if( abs(x) &amp;lt; a, 1, c(x/2)^2-s(x/2)^2 )", a); /* Wskazanie, ze 's' korzysta z 'c', a 'c' korzysta z 's' */ s.addDefinitions(c); c.addDefinitions(s);
Oczekujemy, że im mniejszy parametr $a>0$ tym lepsza aproksymacja funkcji $\sin(x)$ oraz $\cos(x)$ przez odpowiednio $\text{s}(x)$ oraz $\text{c}(x)$. Poniżej wykresy dla $a=0.5$ oraz $a=0.01$.
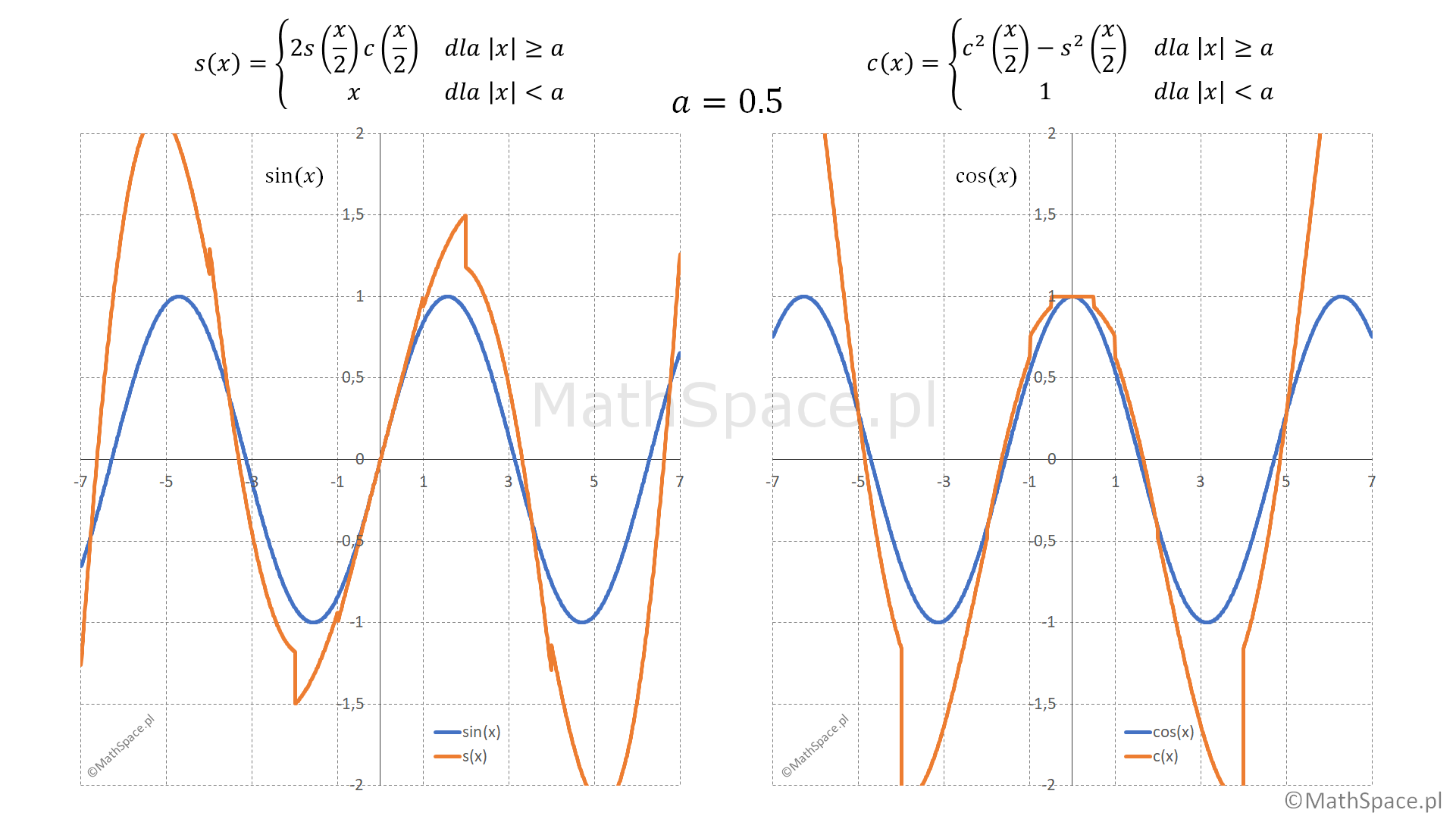
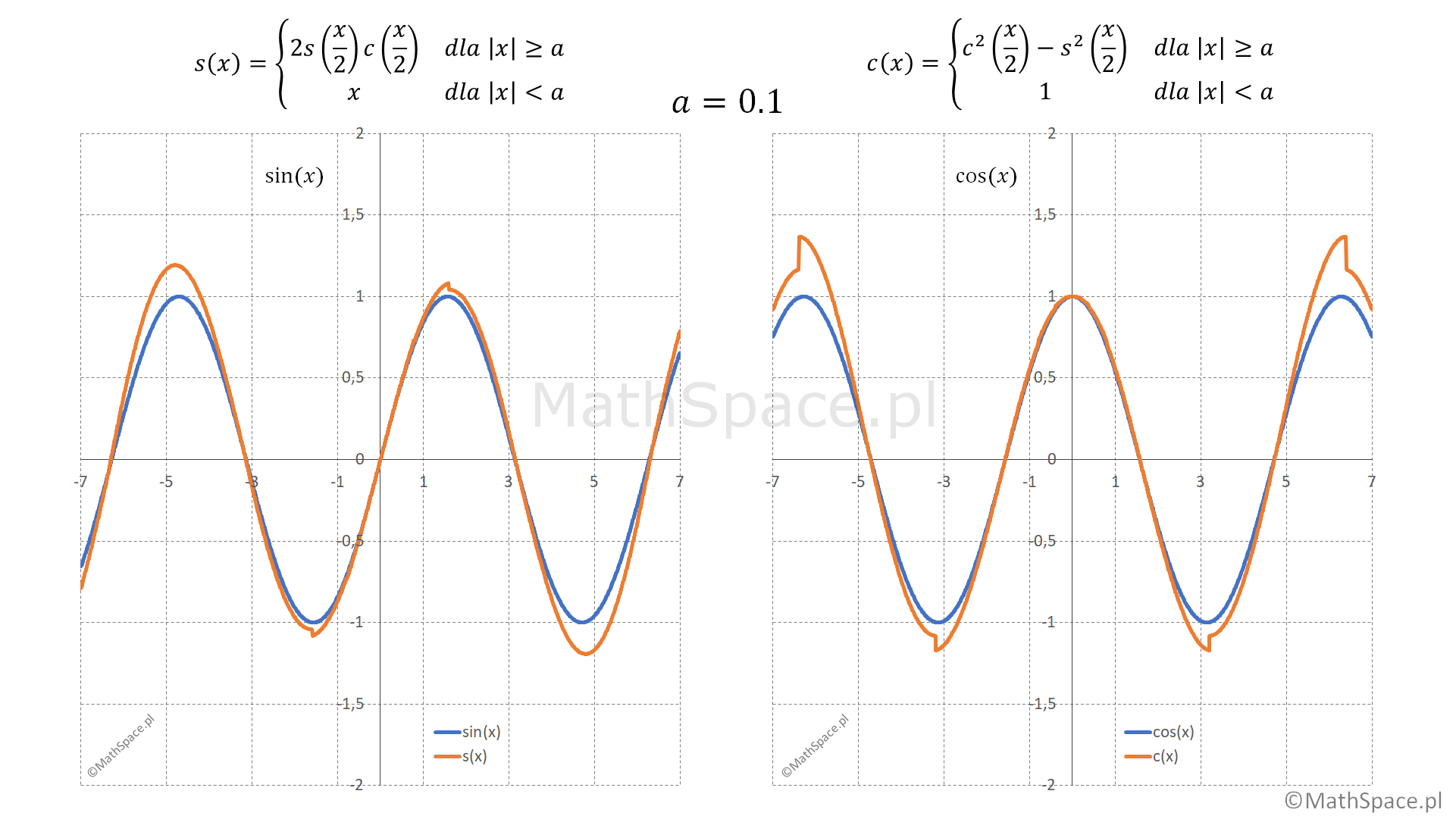
Wniosek – proste zapisy rekurencyjne dają złożone wyniki! 🙂
Rekurencja pośrednia i bezpośrednia – animacja
Pozdrowienia,
Mariusz Gromada
Zobacz również:
- Polowanie na czarownice – czyli zabawy z rekurencją (część 1)
- Prędkość ucieczki do nieskończoności – czyli zabawy z rekurencją (część 2)
- Naiwny test pierwszości – czyli zabawy z rekurencją (część 3)
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.