Dziś zadałem sobie pytanie: jak mają się do siebie wskaźniki Giniego, gdyby je osobno zdefiniować dla klasy pozytywnej „tzn. klasy 1” oraz klasy negatywnej „tzn. klasy 0”? Odpowiedź uzyskałem, czego efektem jest 15 część cyklu „Ocena jakości klasyfikacji”. Tytuł wpisu nawiązuje do faktu, że separację dwóch klas uzyskujemy jednym (i tym) samym modelem 🙂 co poniekąd sugeruje, że … 🙂

… wskaźniki Giniego dla klasy pozytywnej i klasy negatywnej są sobie równe!

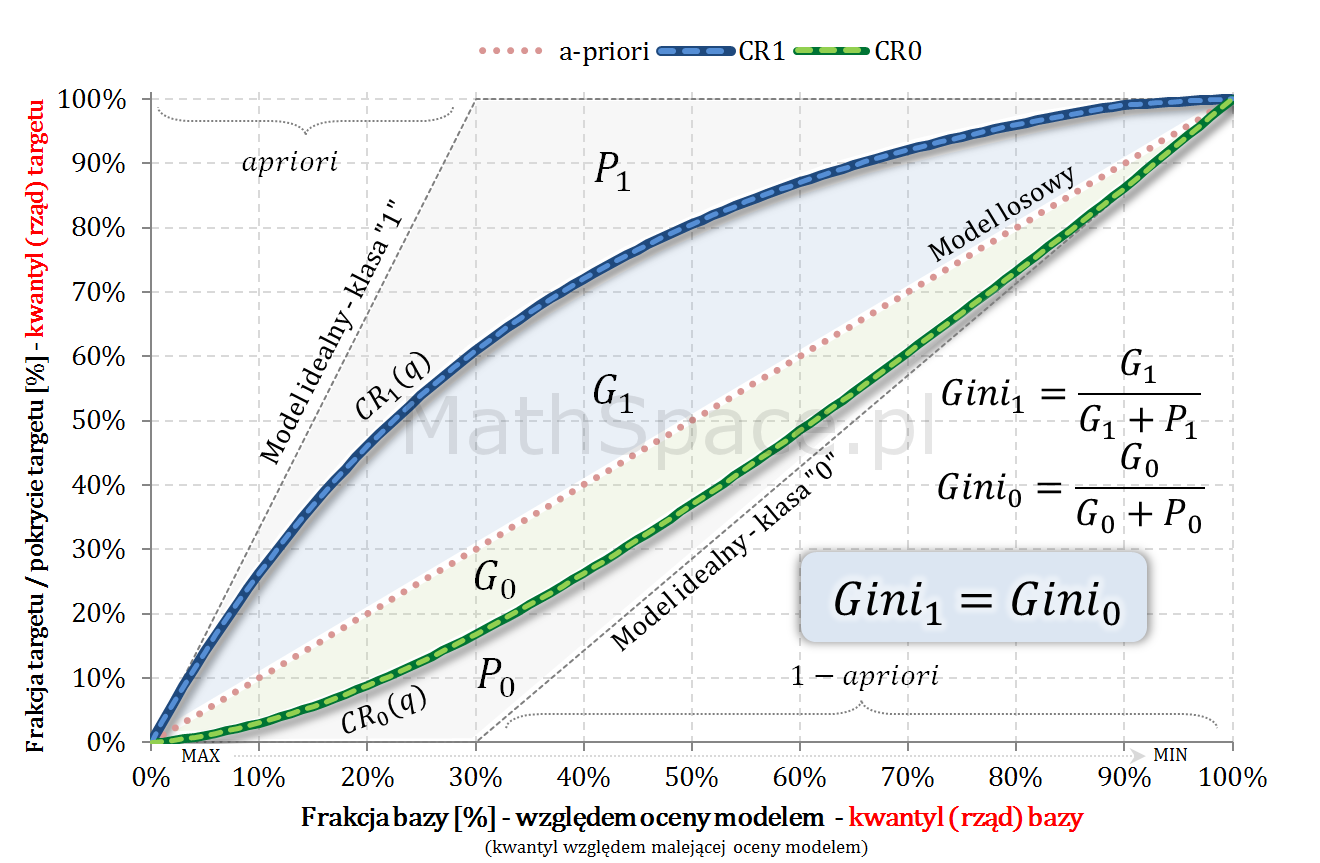
$$Gini_1=\frac{G_1}{G_1+P_1}$$

$$Gini_0=\frac{G_0}{G_0+P_0}$$

$$Gini_1=Gini_0$$

Dowód:

Wykorzystując wzór na pole trójkąta zapisujemy:

$$Gini_1=\frac{G_1}{\quad\frac{1-apriori}{2}\quad}=\frac{2G_1}{1-apriori}$$

$$Gini_0=\frac{G_0}{\quad\frac{apriori}{2}\quad}=\frac{2G_0}{apriori}$$

Zauważamy, że pole $G_0$ można wyznaczyć na bazie różnicy pomiędzy polem trójkąta i polem powierzchni pod krzywą $CR_0$:

$$G_0=\frac{1}{2}-\displaystyle\int_0^1 CR_0(q)dq$$

Korzystając z zależności pomiędzy $CR_1$ oraz $CR_0$ wyprowadzonej w części 14 „Captured Response dla klasy negatywnej” przekształcamy

$$G_0=\frac{1}{2}-\displaystyle\int_0^1\bigg(\frac{q-apriori\times CR_1(q)}{1-apriori}\bigg)dq=$$

$$=\frac{1}{2}-\frac{1}{1-apriori}\displaystyle\int_0^1\bigg(q-apriori\times CR_1(q)\bigg)dq=$$

$$=\frac{1}{2}-\frac{1}{1-apriori}\Bigg(\displaystyle\int_0^1 qdq-apriori\displaystyle\int_0^1 CR_1(q)dq\Bigg)=$$

$$=\frac{1}{2}-\frac{1}{1-apriori}\Bigg[\frac{q^2}{2}\bigg|_0^1-apriori\bigg(G_1+\frac{1}{2}\bigg)\Bigg]=$$

$$=\frac{1}{2}-\frac{1}{1-apriori}\bigg(\frac{1}{2}-apriori\times G_1-\frac{apriori}{2}\bigg)$$

$$=\frac{1}{2}-\frac{1}{2(1-apriori)}+\frac{apriori\times G_1}{1-apriori}+\frac{apriori}{2(1-apriori)}=$$

$$=\frac{1-apriori}{2(1-apriori)}-\frac{1}{2(1-apriori)}+$$

$$+\frac{apriori\times 2G_1}{2(1-apriori)}+\frac{apriori}{2(1-apriori)}=$$

$$=\frac{1-apriori-1+apriori\times 2G_1+apriori}{2(1-apriori)}=$$

$$=\frac{apriori\times 2G_1}{2(1-apriori)}=$$

$$=\frac{apriori}{2}\times\frac{2G_1}{1-apriori}=$$

$$=\frac{apriori}{2}\times Gini_1$$

$$G_0=\frac{apriori}{2}\times Gini_1$$

Ale

$$Gini_0=\frac{2G_0}{apriori}=$$

$$=\frac{2}{apriori}\times G_0=\frac{2}{apriori}\times\frac{apriori}{2}\times Gini_1$$

$$Gini_0=Gini_1$$

cbdo 🙂

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.