Witaj w 14 części cyklu „Ocena jakości klasyfikacji”. Dziś rozwinę wątek oszacowania separacji klas na bazie krzywej Captured Response – będzie to kolejny odcinek z serii „Tips & Tricks na krzywych”.

Statystyka KS Kołmogorowa-Smirnowa jako miara różnicy rozkładów

Rozważmy dwie rzeczywiste zmienne losowe $X_1$ i $X_2$ oraz ich dystrybuanty odpowiednio $F_{X_1}$ oraz $F_{X_2}$. Statystyką Kołmogorowa-Smirnowa dla zmiennych $X_1$ oraz $X_2$ nazywamy odległość $D\big(X_1,X_2\big)$ zdefiniowaną następująco:

$$D\big(X_1,X_2\big)=\displaystyle\sup_{x\in\mathbb{R}}\bigg|F_{X_1}(x)-F_{X_2}(x)\bigg|$$

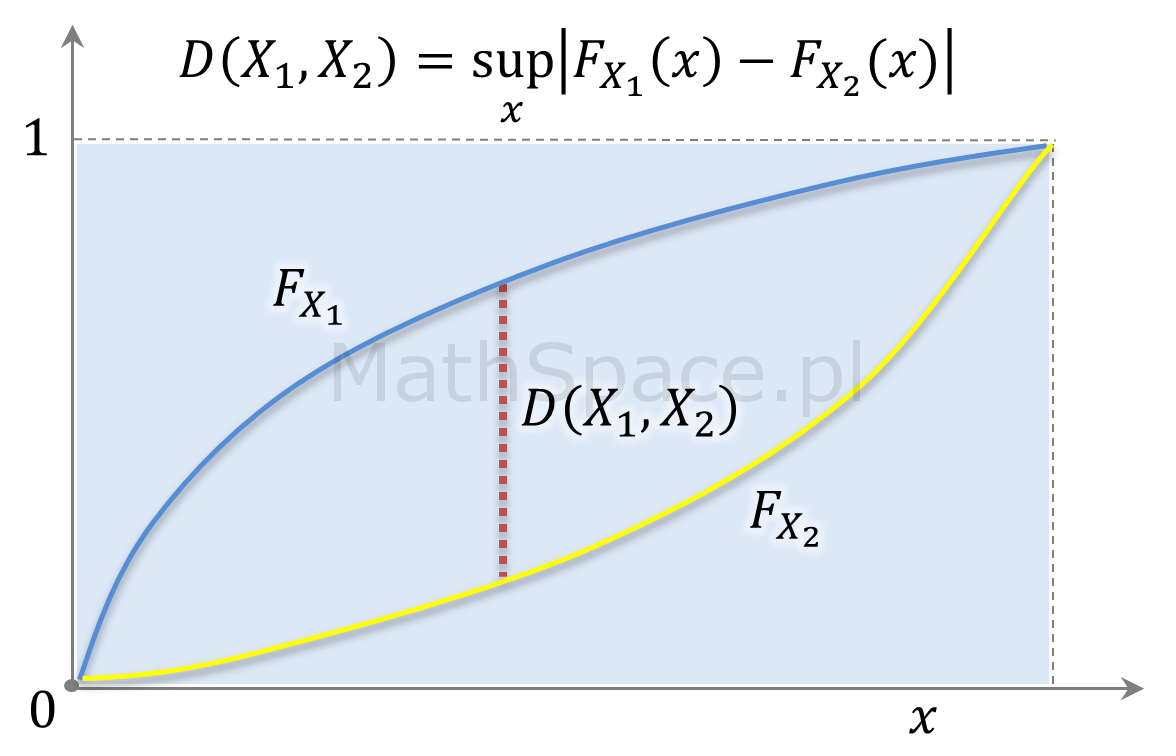
Jeśli $x$ jest badaną wartością, to odległość KS interpretujemy jako maksymalną różnicę pomiędzy rzędem kwantyla w rozkładzie pierwszym i rzędem kwantyla w rozkładzie drugimi, które to rzędy odpowiadają wspólnej wartości $x$.

Do tanga trzeba dwojga

Przy modelach predykcyjnych, dla problemu klasyfikacji binarnej, tak naprawdę dysponujemy trzema rozkładami:

• rozkład populacji / próby względem oceny modelem;
• rozkład klasy pozytywnej względem oceny tym samym modelem;
• rozkład klasy negatywnej również względem oceny tym samym modelem.

W części #13 „Lift i Captured Response to gęstość i dystrybuanta tego samego rozkładu” pokazałem jak „wygląda” rozkład klasy pozytywnej. Dziś interesuje nas odległość KS rozkładu „jedynek” od rozkładu „zer”, przechodzimy więc do zdefiniowana gęstości i dystrybuanty dla klasy negatywnej.

Lift nieskumulowany dla klasy negatywnej – tzn. „klasy 0”

Załóżmy, że dana jest funkcja $Lift.Niesk_1(\Delta q)$ liftu nieskumulowanego dla klasy pozytywnej, gdzie $\Delta q$ to przedział rzędu kwantyla (w całej populacji) względem malejącej oceny modelem.

$$Lift.Niesk_0(\Delta q)=\frac{P(0|\Delta q)}{P(0)}$$

$$Lift.Niesk_0(\Delta q)=\frac{1-P(1|\Delta q)}{1-P(1)}=$$

$$=\frac{1-P(1)\frac{P(1|\Delta q)}{P(1)}}{1-P(1)}=$$

$$=\frac{1-P(1)\cdot Lift.Niesk_1(\Delta q)}{1-P(1)}$$

$$Lift.Niesk_0(\Delta q)=\frac{1-apriori\times Lift.Niesk_1(\Delta q)}{1-apriori}$$

Przykład dla pewnej funkcji liftu nieskumulowanego i apriori = 30%.

Warto zwrócić uwagę na punkt przecięcia tych krzywych – spotykają się w tym samym miejscu, gdzie dochodzi do zrównania z krzywą dla modelu losowego. Dosyć łatwo to uzasadnić: jeśli $P(1|\Delta q^i)=apriori$ to $P(0|\Delta q^i)=1-apriori$.

Sprawdźmy jeszcze czy $Lift.Niesk_0(\Delta q)$ spełnia warunek „unormowania”.

$$\displaystyle\int_0^1 Lift.Niesk_0(q)dq=$$

$$=\displaystyle\int_0^1 \frac{1-apriori\times Lift.Niesk_1(q)}{1-apriori}dq=$$

$$=\frac{1}{1-apriori}\displaystyle\int_0^1 \bigg(1-apriori\times Lift.Niesk_1(q)\bigg)dq=$$

$$=\frac{1}{1-apriori}\bigg(\displaystyle\int_0^1 1dq-apriori\displaystyle\int_0^1Lift.Niesk_1(q)dq\bigg)=$$

$$=\frac{1}{1-apriori}(1-apriori)=1$$

$$\displaystyle\int_0^1 Lift.Niesk_0(q)dq=1$$

Captured Response dla klasy negatywnej – tzn. „klasy 0”

Załóżmy, że dana jest funkcja $CR_1(q)$ Captured Response dla klasy pozytywnej, gdzie $q$ to rząd kwantyla (w całej populacji) względem malejącej oceny modelem.

Oznaczenia:

• $q$ – punkt, dla którego wyznaczamy wartość krzywej;
• $N=N_1+N_0$ – liczba obserwacji: łączna, z „klasy 1”, z „klasy 0”;
• $n=n_1+n_2=q\cdot N$ – liczba obserwacji „na lewo” od $q$: łączna, z „klasy 1”, z „klasy 0”;

Wtedy:

$$CR_1(q)=\frac{n_1}{N_1}$$

$$CR_0(q)=\frac{n_0}{N_0}$$

Wyprowadzamy $CR_0(q)$ w zależności od $CR_1(q)$.

$$CR_0(q)=\frac{n_0}{N_0}=\frac{n-n_1}{N_0}=\frac{n-N_1\frac{n_1}{N_1}}{N_0}=$$

$$=\frac{n-N_1 CR_1(q)}{N_0}=\frac{qN-N_1 CR_1(q)}{N_0}=$$

$$=\frac{qN}{N_0}+\frac{N_1 CR_1(q)}{N_0}=q\bigg(\frac{N_0}{N}\bigg)^{-1}-\frac{N_1}{N_0}CR_1(q)=$$

$$=\frac{q}{1-apriori}-\frac{N_1 N}{NN_0}CR_1(q)=0$$

$$=\frac{q}{1-apriori}-\frac{N_1}{N}\bigg(\frac{N_0}{N}\bigg)^{-1}CR_1(q)=$$

$$=\frac{q}{1-apriori}-apriori\frac{1}{1-apriori}CR_1(q)$$

$$CR_0(q)=\frac{q-apriori\times CR_1(q)}{1-apriori}$$

Przykład dla pewnej funkcji Captured Response i apriori = 30%.

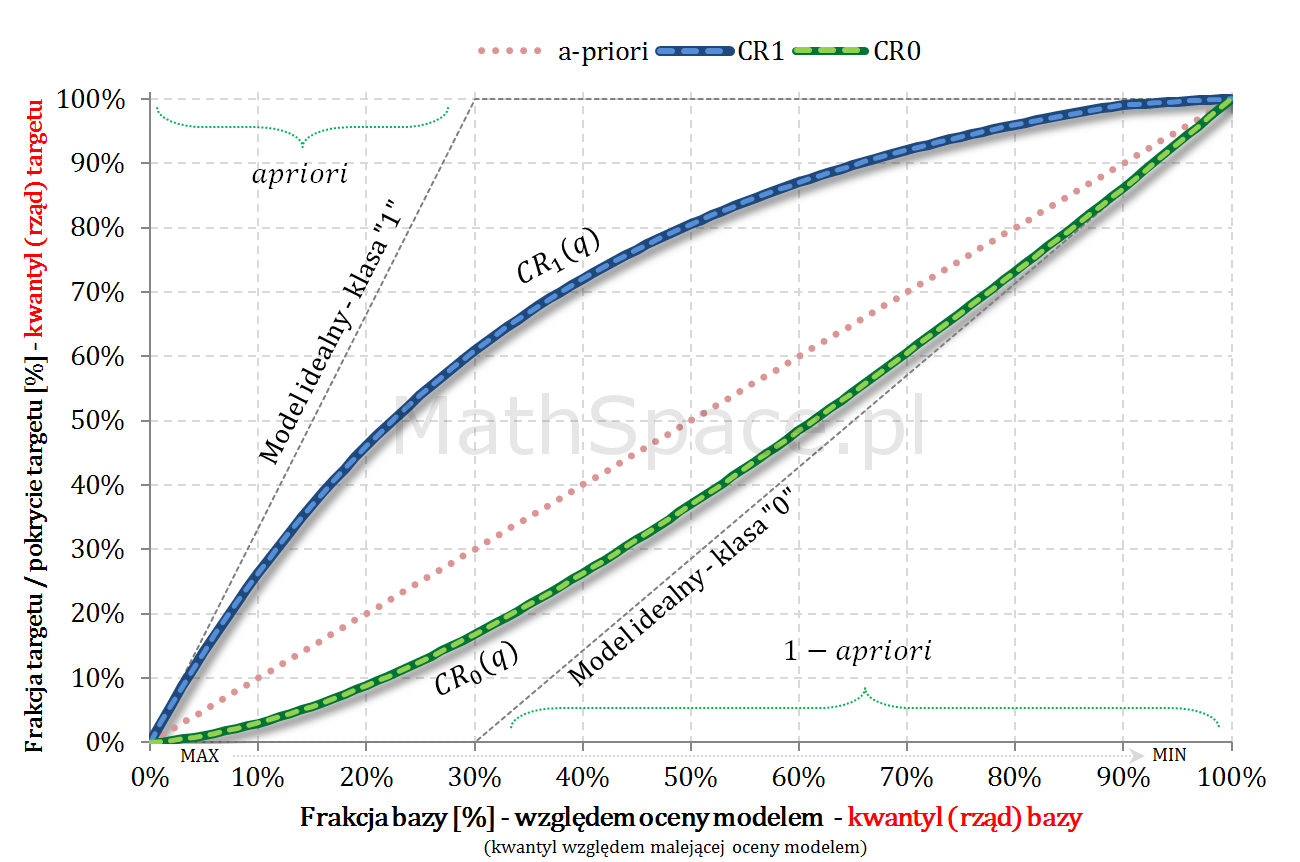
$CR_0(q)$ jest dystrybuantą, gdyż:

• $CR_0(0)=\frac{0-apriori\times CR_1(0)}{1-apriori}=\frac{0-apriori\times 0}{1-apriori}=0$
• $CR_0(1)=\frac{1-apriori\times CR_1(1)}{1-apriori}=\frac{1-apriori\times 1}{1-apriori}=1$
• Jest funkcją niemalejącą, co wynika bezpośrednio z jej definicji.

Lift nieskumulowany dla klasy negatywnej to pochodna Captured Response dla klasy negatywnej

$$CR_0^\prime(q)=\bigg(\frac{q-apriori\times CR_1(q)}{1-apriori}\bigg)^\prime=$$

$$=\frac{\big(q-apriori\times CR_1(q)\big)^\prime}{1-apriori}=\frac{1-apriori\times CR_1^\prime(q)}{1-apriori}=$$

$$=\frac{1-apriori\times Lift.Niesk_1(q)}{1-apriori}=Lift.Niesk_0(q)$$

$$CR_0^\prime(q)=Lift.Niesk_0(q)$$

Aby w pełni zrozumieć powyższe przejścia zapoznaj się z częścią #11 „Captured Response vs Lift”, gdzie uzasadniam, że pochodna Captured Response to lift nieskumulowany.

Wniosek: Lift nieskumulowany dla klasy negatywnej oraz Captured Response dla klasy negatywnej to gęstość i dystrybuanta tego samego rozkładu.

Jeśli

$$Q=(q_1,q_2)$$

to

$$P(q\in Q|0)=\displaystyle\int_{q_1}^{q_2}Lift.Niesk_0(q)dq=$$

$$=CR_0(q_2)-CR_0(q_1)$$

$$P(q\in Q|1)=\displaystyle\int_{q_1}^{q_2}Lift.Niesk_1(q)dq=$$

$$=CR_1(q_2)-CR_1(q_1)$$

Wskaźnik KS dla $CR_1$ i $CR_0$ – czyli miara separacji klas

Wskaźnik KS dla $CR_1$ i $CR_0$ zdefiniujemy następująco:

$$D\big(CR_1,CR_0\big)=\displaystyle\sup_{q\in[0,1]}\bigg|CR_1(q)-CR_0(q)\bigg|$$

Równoważnie poszukujemy takiego $q_{max}\in[0,1]$, że

$$D\big(CR_1,CR_0\big)=\displaystyle\sup_{q\in[0,1]}\bigg|CR_1(q)-CR_0(q)\bigg|=$$

$$=CR_1(q_{max})-CR_0(q_{max})$$

Zauważmy, że

$$CR_1(q)-CR_0(q)=\bigg(CR_1(q)-q\bigg)+\bigg(q-CR_0(q)\bigg)$$

Badamy przebieg zmienności – a konkretnie typujemy punkt maksimum na podstawie pochodnej.

Dla klasy „1”:

$$\bigg(CR_1(q)-q\bigg)^\prime=0$$

$$CR_1^\prime(q)=1$$

$$Lift.Niesk_1(q)=1$$

Dla klasy „0”:

$$\bigg(q-CR_0(q)\bigg)^\prime=0$$

$$CR_0^\prime(q)=1$$

$$Lift.Niesk_0(q)=1$$

$$\frac{1-apriori\times Lift.Niesk_1(q)}{1-apriori}=1$$

$$1-apriori\times Lift.Niesk_1(q)=1-apriori$$

$$-apriori\times Lift.Niesk_1(q)=-apriori$$

$$apriori\times Lift.Niesk_1(q)=apriori$$

$$Lift.Niesk_1(q)=1$$

Wniosek: odległość $CR_1(q)-CR_0(q)$ jest maksymalizowana w punkcie, w którym funkcja liftu nieskumulowanego ma wartość 1 – tzn. w punkcie przecięcia z liftem dla modelu losowego.

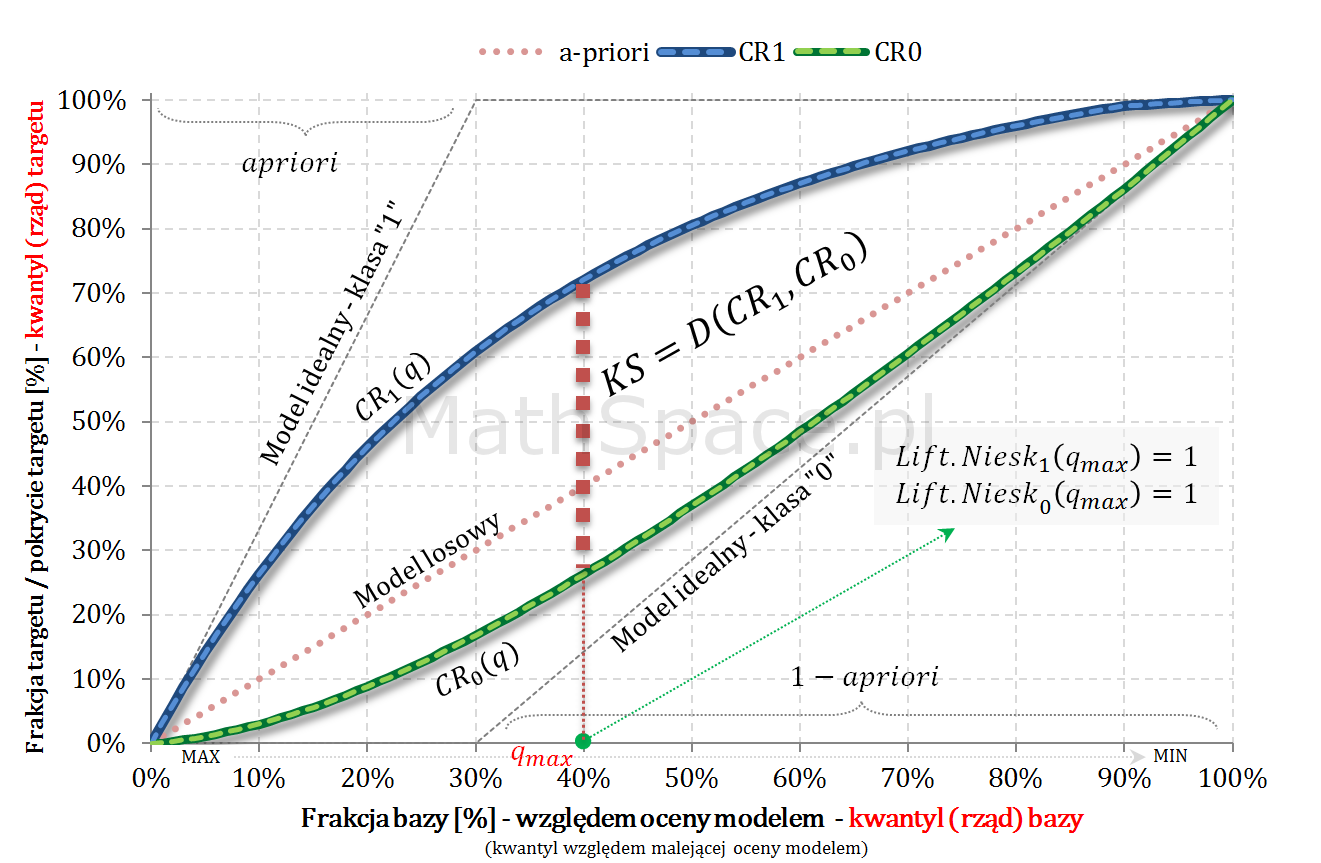
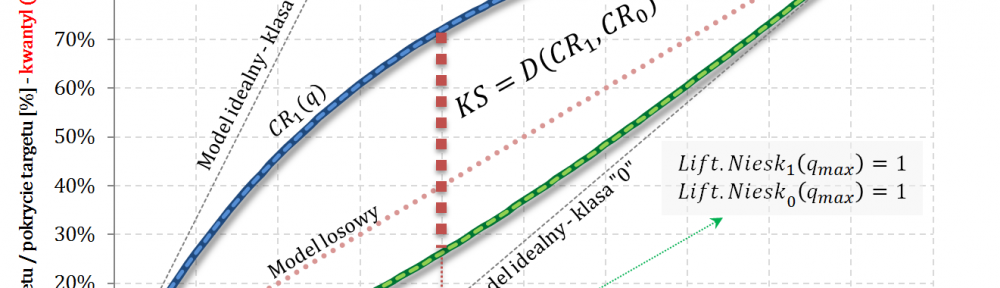
Powyższy wniosek jest dosyć intuicyjny – jeśli lift nieskumulowany „wchodzi w obszar bycia mniejszym niż 1” oznacza to, że jego efekt jest mniejszy od działania modelu losowego. Dodawanie kolejnych obserwacji zaczyna zmniejszać separację rozkładów.

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa