Właśnie czytasz część #9 cyklu „Ocena jakości klasyfikacji” – a to oznacza, że posiadasz już sporą wiedzę – i masz ochotę na więcej – gratuluję! 🙂
Korelacja rangowa … czy to wystarczy?
W częściach 1-8 skupiałem się na analizie korelacji rangowej. W tym przypadku korelacja rangowa odpowiada na pytanie „jak dobrze uporządkowany jest target w zależności od oceny modelem” – tzn. jak silnie monotoniczna jest zależności pomiędzy score i targetem? Innymi słowy – czy wraz ze wzrostem score, rośnie frakcja True-Positive, i jak silny jest to wzrost? Krzywa lift, czy Captured Response, doskonale to obrazują. Jednak to nie wszystko … W wielu przypadkach niezbędne jest prawidłowe oszacowanie prawdopodobieństwa z jakim zaobserwujemy klasę pozytywną.
Ocena estymacji prawdopodobieństwa – co to?
Załóżmy, że określoną grupę klientów podzieliśmy na dane trenujące i uczące oraz, że na próbie uczącej przygotowaliśmy model predykcyjny szacujący prawdopodobieństwo „bycia klasą pozytywną”. Przyjmijmy, że dla pewnego klienta x model zwrócił prawdopodobieństwo 0.3. W tym przypadku wskaźnik 0.3 oznacza, że np. dla 100 klientów, o tych samych cechach, spodziewamy się około 30 z „klasy pozytywnej” oraz około 70 z „klasy negatywnej”. Ocena estymacji prawdopodobieństwa to weryfikacja na ile możemy ufać oszacowaniu, tutaj 30 vs 70.
W ogólności – chodzi o stwierdzenie czy estymator (czyli nasz model) jest nieobciążony (czyli wolny od błędu systematycznego), a jeżeli jest obciążony, to na ile i w jakich przypadkach. Statystyka matematyczna dostarcza szeregu różnych wskaźników wyznaczających błąd oszacowania dla zmiennej ciągłej – np. błąd średnio-kwadratowy – w tym tekście nie będę się na nich skupiał. Nasz przypadek jest mniej ogólny, a i samej weryfikacji najwygodniej dokonać „organoleptycznie” – tzn. metodą wizualną w wielu krokach 🙂
Kiedy oceniać jakość estymacji prawdopodobieństwa?
Generalnie zawsze! Często same techniki modelowania optymalizują prawdopodobieństwo – np. regresja logistyczna wykorzystująca metodę największej wiarygodności – tu konieczność badania jest oczywista. Inne metody, takie jak drzewa decyzyjne, wraz ze wzrostem drzewa, starają się zmniejszyć zmienność klas w węzłach potomkach / liściach – tu nadal możemy ocenić finalne prawdopodobieństwo – np. na bazie rozkładu klas (o ile liczności są odpowiednio duże). Zasada jest taka – ocena prawdopodobieństwa daje zawsze dodatkową cenną informację w procesie weryfikacji jakości modelu! Jest jednak kilka szczególnych przypadków, kiedy ocena poprawności prawdopodobieństwa jest absolutnie konieczna:
- Model będzie stosowany w wyznaczaniu wartości oczekiwanych (np. oczekiwany przychód).
- Kwestie regulacyjne / modele ryzyka kredytowego (np. modele PD – Probability Default).
- Modele Anti-Fraud.
- Modele churn (np. oczekiwana wartość utracona).
- Modele up-lift (np. efekt inkrementalny na bazie różnicy dwóch modeli) – o tym opowiemy kiedyś w szczegółach.
- Rekomendatory na bazie „głosowania” modelami propensity (modelami skłonności do skorzystania z produktu / usługi).
- I wiele innych …
Tarcza prawdopodobieństwa – typowe sytuacje w praktyce
Tarcza prawdopodobieństwa – nazwa moja, nie szukajcie po Wikipedii 🙂 – to ciekawe i proste narzędzie obrazujące schematycznie (w dalszej części również praktycznie) typowe przypadki, na jakie z pewnością natkniecie się w pracy z rzeczywistymi modelami. Czasami jeden obraz wart jest znacznie więcej niż potok słów – zatem zaczynamy.
Silny model – schemat
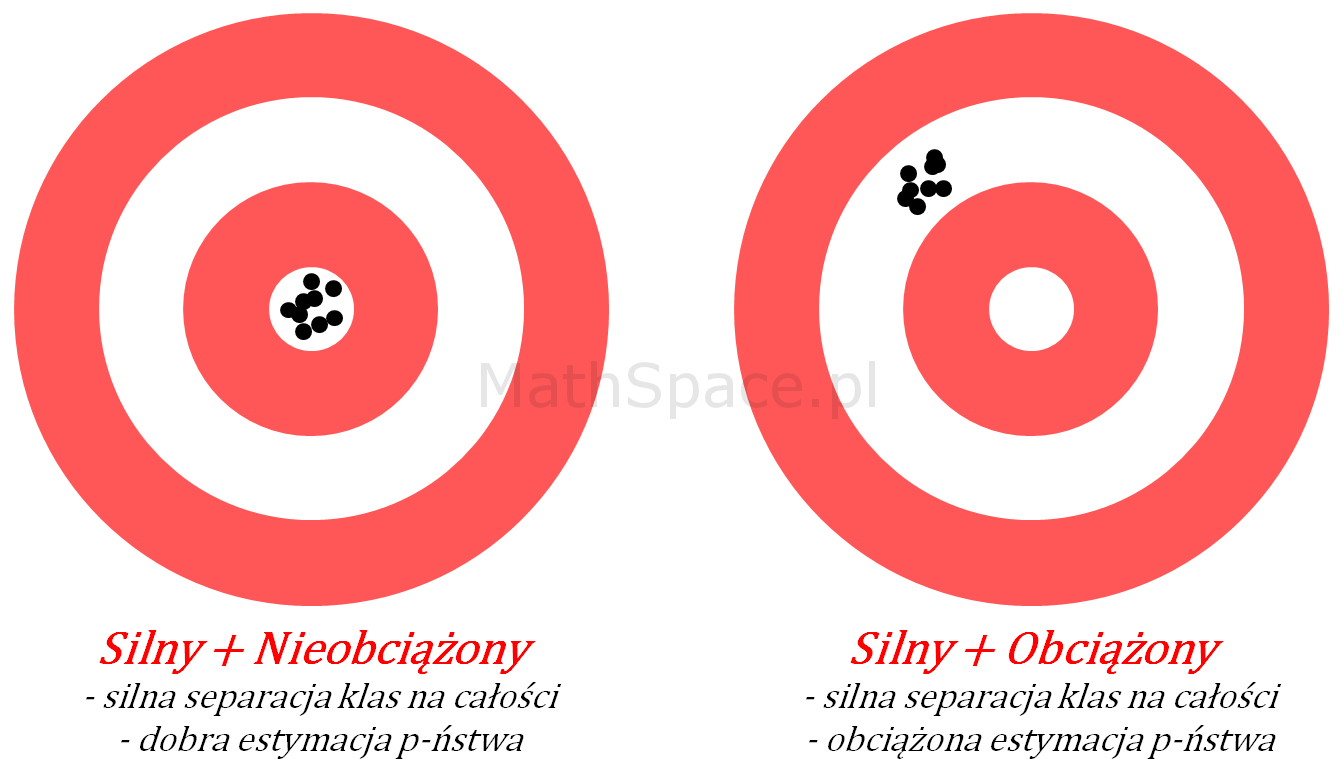
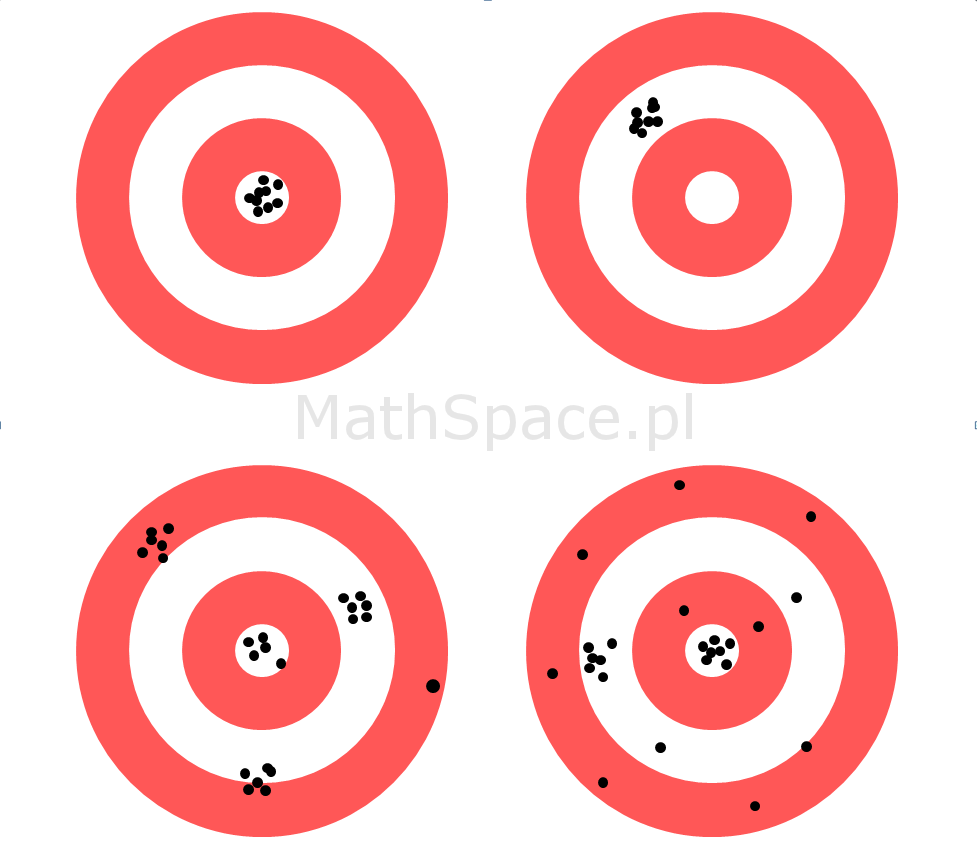
- Przypadek 1: Silny model z dobrą estymacją prawdopodobieństwa
Schemat obrazuje sytuację, kiedy model trafia „w punkt” – czyli powtarzalnie i precyzyjnie odróżniany jest „cel” od reszty „tarczy”. Świadczy to o wysokiej separacji klas (klasa pozytywna vs klasa negatywna), spodziewany wysoki indeks Giniego, jak też oczekiwana dobra jakość estymacji prawdopodobieństwa. Na schemacie „centrum” jest tym miejscem, w które trafia model.
Akcja: Model gotowy do wykorzystania.
- Przypadek 2: Silny model z obciążoną estymacją prawdopodobieństwa
Tym razem schemat przedstawia model o wysokim skupieniu – czyli mamy dużą powtarzalność wyników wraz z ich skupieniem, natomiast samo skupienie jest przesunięte w stosunku do punktu środkowego. Interpretacja – mamy do czynienia z silną separacją klas (wysoki indeks Giniego), natomiast szacowanie prawdopodobieństwa obarczone jest systematycznym błędem (obciążeniem).
Akcja: Model wymaga kalibracji, może być warunkowo stosowany w sytuacjach, kiedy opieramy się wyłącznie na korelacji rangowej.
Model z siłą predykcyjną w ograniczeniu do podgrup – schemat
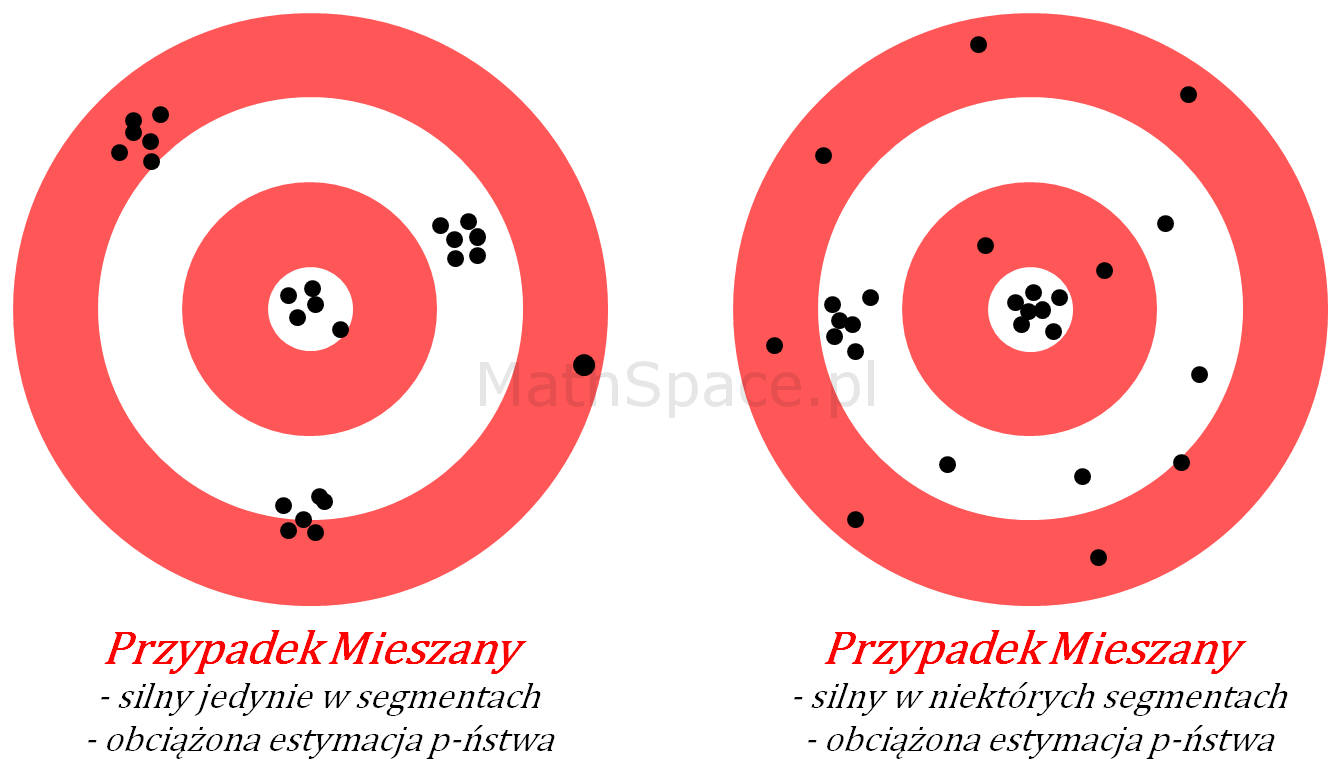
- Przypadek 1: Silny model w ograniczeniu do podgrup
Sytuacja nieco bardziej złożona. Model, jako całość, nie jest zbyt dobry, natomiast w ograniczeniu do pewnych segmentów (np. klient „młody”, klient „zamożny”, etc…) separacja klas jest wysoka. Niestety, w tych segmentach, estymacja prawdopodobieństwa jest obarczona błędem systematycznym, co skutkuje niską siłą modelu dla całej populacji.
Akcja: Model wymaga dalszych prac, typowo niezbędne jest przygotowanie osobnych modeli dla wskazanych segmentów, następnie połączenie ich w całość.
- Przypadek 2: Silny model wyłącznie dla wybranych segmentów
Podobnie jak wyżej, z tą różnicą, że istnieją podgrupy, w których model traci siłę separacji klas.
Akcja: Model wymaga dalszych prac, być może został popełniony błąd w kodzie i/lub w przetwarzaniu danych. Sprawdź cały eksperyment.
Słaby model – schemat
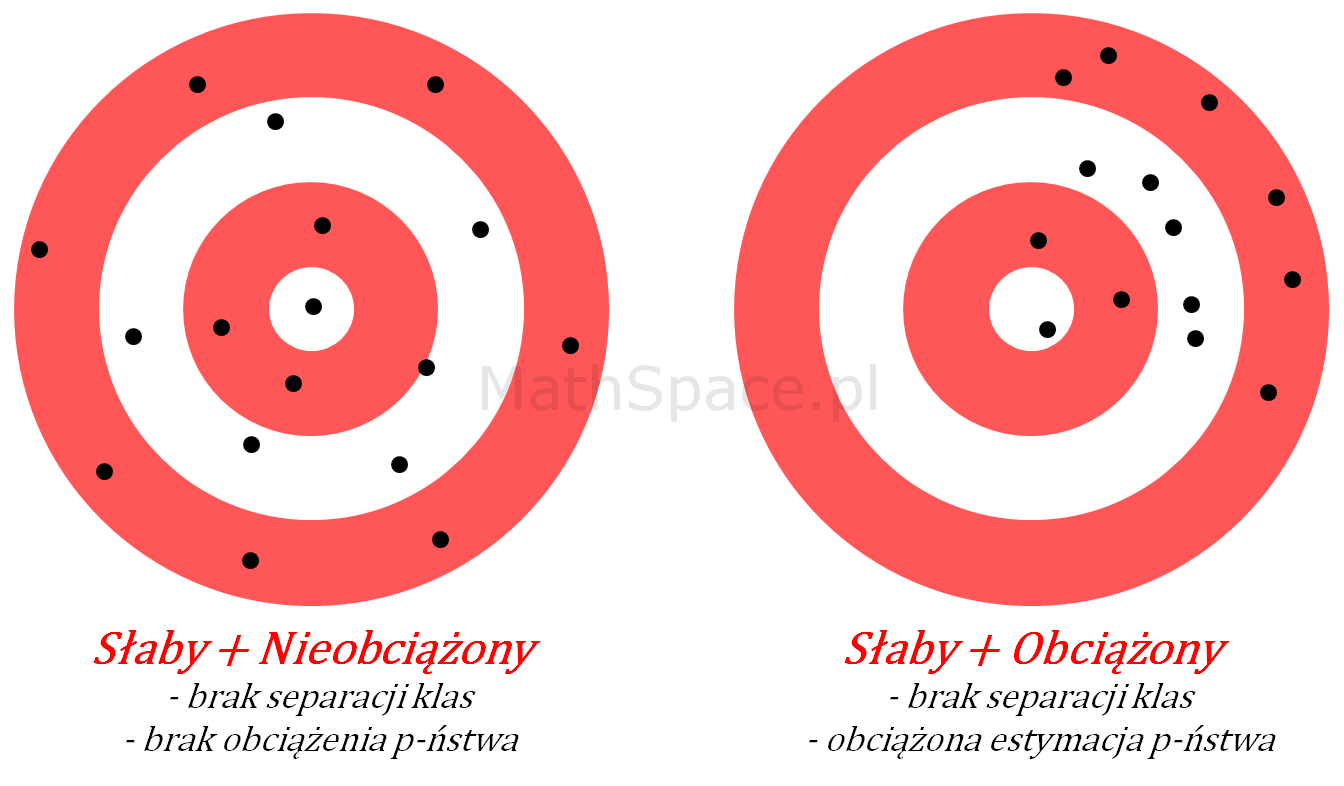
„Model strzela na oślep”, trafienia są nieprzewidywalne, nie ma skupienia. Interpretacja – brak separacji klas, indeks Giniego bardzo niski. Samo prawdopodobieństwo może być nieobciążone, tzn. średnia może zgadzać się z oczekiwanym a-priori.
Akcja: Zdecydowanie sytuacja negatywna, należy powtórzyć całość eksperymentu – prawdopodobnie błąd w kodzie, błąd w danych, błąd w założeniach, ewentualnie (choć mniej prawdopodobne) zmienne nie posiadają siły predykcyjnej.
Tarcza prawdopodobieństwa – praktyczna realizacja
Wizualizacja tarczy, aby ocena mogła być dokonana wiarygodnie, wymaga odpowiedniej liczby „strzałów”. Proponuję stosować wykres zawierający 100 punktów, każdy dla osobnego centyla score (przy założeniu, że mamy odpowiednio dużo danych wejściowych).
Kroki:
- Dane testowe (osobno uczące) dzielimy na 100 grup, gdzie każda grupa to centyl względem rosnącej wartości szacowanego prawdopodobieństwa (score).
- W każdej grupie wyznaczamy frakcję klasy pozytywnej.
- W każdej grupie wyznaczamy średnie estymowane prawdopodobieństwo (średni score).
- Wykres:
- oś pozioma „X”: frakcja klasy pozytywnej
- oś pionowa „Y” średni score.
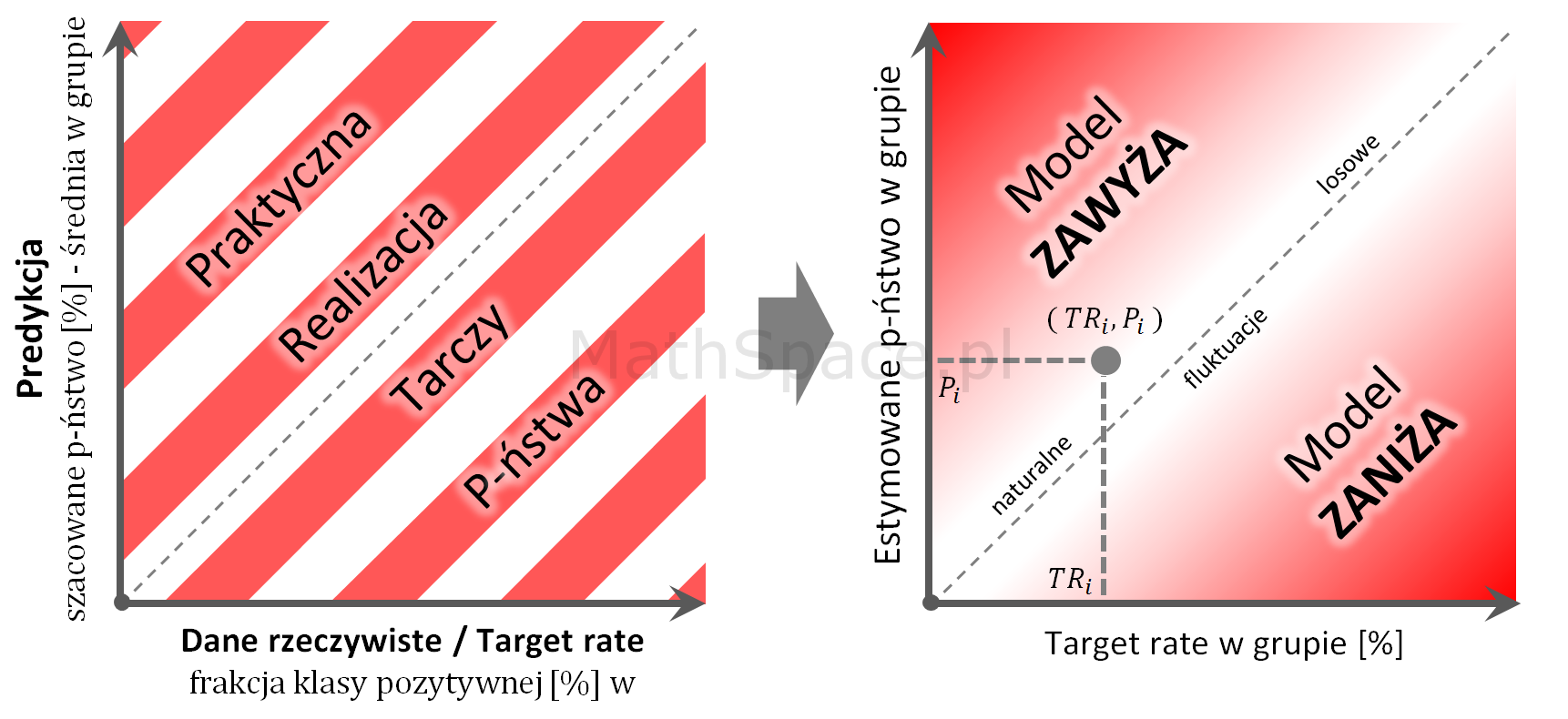
- $TR_i$ – target rate w grupie „i”
- $P_i$ – estymowane prawdopodobieństwo w grupie „i”
Interpretacja:
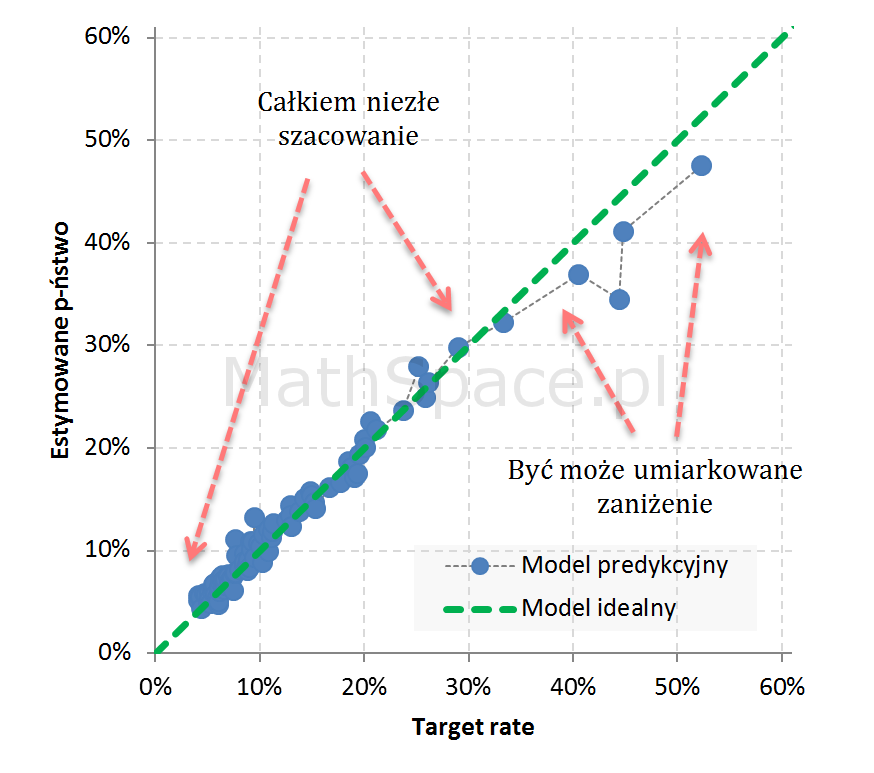
- Model idealny znajduje się na prostej y = x (tzn. brak błędu estymacji prawdopodobieństwa).
- Model praktycznie dobry powinien dawać wyniki „w pobliżu” prostej y = x, przy czym „wahania pod / nad prostą” powinny charakteryzować się losowością, co świadczy o braku obciążenia.
- Przestrzeń nad prostą y = x to obszar, gdzie model zawyża prawdopodobieństwo.
- Przestrzeń pod prostą y = x to obszar, gdzie model zaniża prawdopodobieństwo.
Typowe proces oceny jakości estymacji prawdopodobieństwa
- Ocena dla całej populacji: średni score vs a-priori / target rate całej populacji.
- Ocena dla głównych segmentów: jeśli pracujemy na rzeczywistych obiektach (np. zbiór klientów) typowo dysponujemy szeregiem łatwych w interpretacji cech, które generują naturalne segmenty – będą to np.: wiek, płeć, miejsce zamieszkania (populacja), posiadane produkty, klient zamożny, klient indywidualny, i wiele innych. Często model szacuje prawidłowe prawdopodobieństwo dla całej populacji, niestety myląc się w podgrupach.
- Ocena na bazie „tarczy prawdopodobieństwa”: tym razem zadajemy pytanie czy błąd estymacji zależy od wartości score? Idealna sytuacja jest tak, że nie zależy, tzn. że błąd pojawia się losowo. Score jest wypadkową szeregu zmiennych, więc pośrednio pokazujemy, że błąd zależy / nie zależy od każdej ze zmiennych osobno.
Przykłady
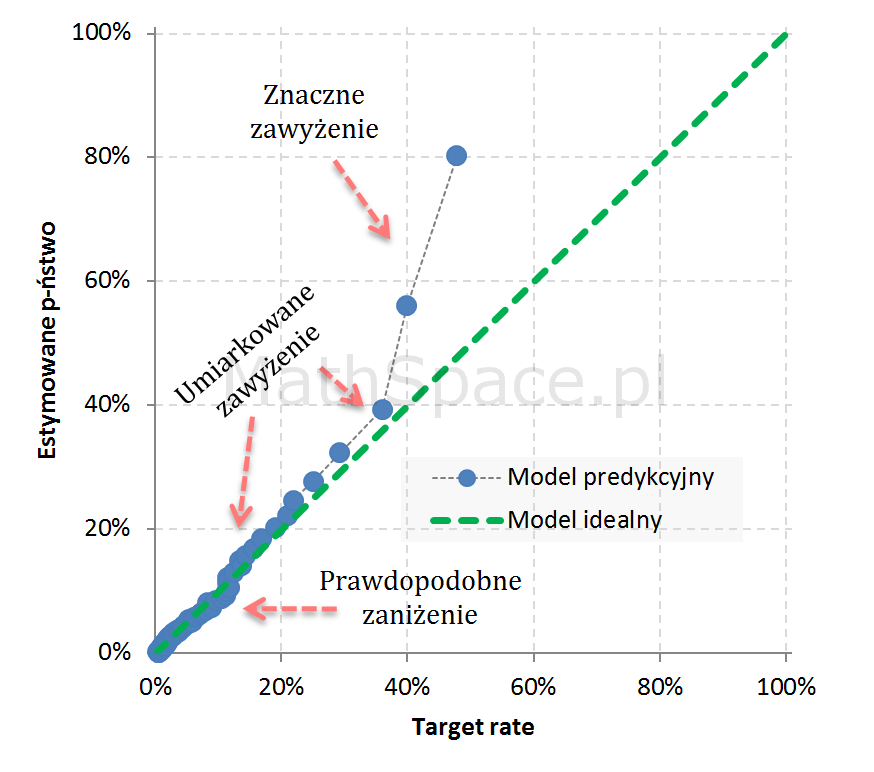
Przykład 1: Estymacja silnie zawyżona w segmentach wysokiego prawdopodobieństwa (wysokiej skłonności)
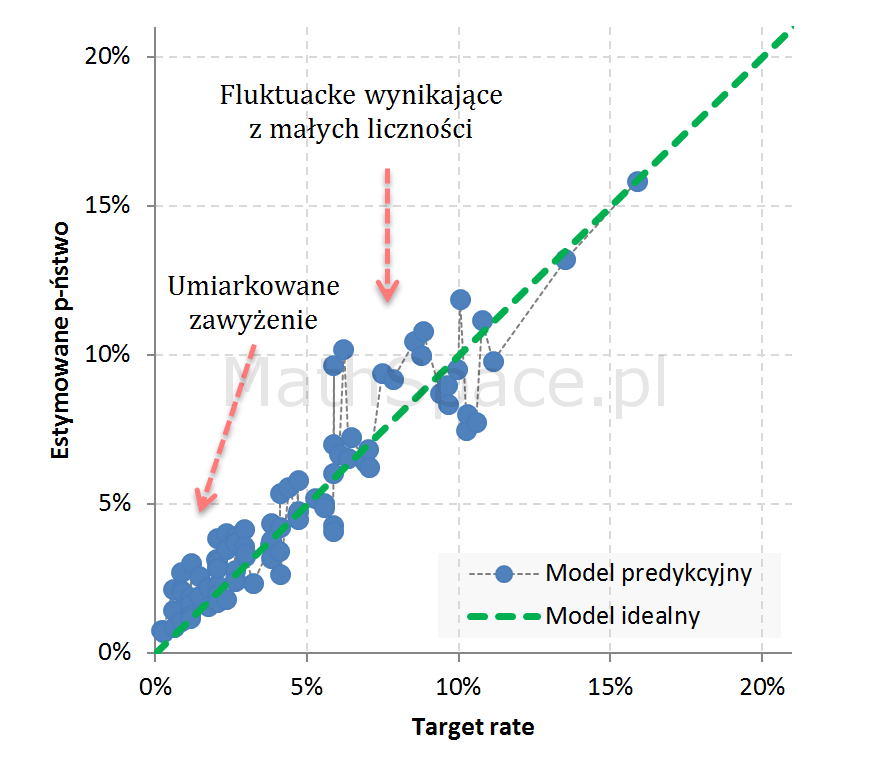
Przykład 2: Umiarkowane zawyżenie w segmentach niskiego prawdopodobieństwa
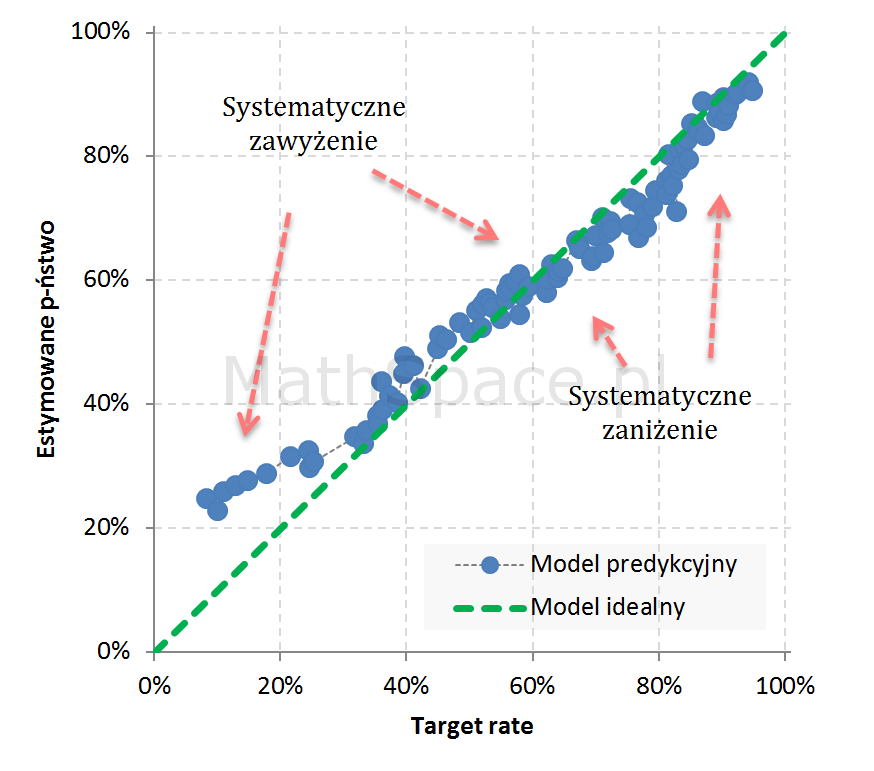
Przykład 3: Widoczne 3 segmenty z obciążeniem: 1. dość istotne zawyżenie, 2. umiarkowane zawyżenie, 3. umiarkowane zaniżenie
Przykład 4: Całkiem niezły model
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.


Cześć,
Bardzo lubię twoją serię, pokazuję ją kolegom w pracy jako referencje do oceny jakości klasyfikacji.
Fajnie by było jakbyś pod artykułami załączał jakąś literaturę, albo literaturę uzupełniającą do tematu.
Cześć Mateusz,
Dzięki za miłe słowa – to bardzo ważne dla mnie, daje motywację. W kwestii literatury – dodam to po części 10, która zamknie cykl i otworzy pewnie nowy 🙂 Będzie to zbiorcza informacja o różnych dostępnych źródłach.
Pozdrowienia
Cześć, jeszcze jedno pytanie, tym razem bardziej związane z przedstawionym tematem. Czy istnieje jakaś miara jakości zgodności prawdopodobieństwa? w przypadku krzywych ROC możemy używać wskaźnik Giniego algo AUROC. Dosyć naturalnym wydaje się tu być test zgodności chi-kwadrat i wartość statystyki testowej jaka miara zgodności. Wiesz coś może w tej materii?
Cześć. Model to estymator, więc wszystkie miary oceny jakości estymacji będą działały. Można zastosować również metody szeregów czasowych. Mi się jednak wydaje, że „przyjrzenie” się wykresom jest najważniejsze. W kolejnych odcinkach napiszę o prognozowaniu Lift, ROC, CR i wskaźnika Giniego. Różnica pomiędzy prognozą Giniego a jego faktyczną wartością może być pewną miarą, choć są sytuacje wątpliwe. Pozdrowienia
Bardzo interesujący blog!
Z niemałym zainteresowaniem śledzę go już od pewnego czasu i nie ukrywam, że trafia do mnie przystępność Pana opracowań i tłumaczeń.
Pana bogata wiedza z pewnością przyda się wielu czytelnikom, tych zaś, którzy czują mimo tego lekki niedosyt pozwolę sobie odesłać do jeszcze innego portalu (http://www.statystyka.az.pl), którym również często się posiłkuję w zakresie wiedzy statystycznej. To naprawdę spora skarbnica informacji!
Bardzo dziękuję 🙂