Funkcja wykładnicza i logarytm wprowadzane są w szkole średniej (przynajmniej tak było w moim przypadku). Zazwyczaj wtedy poznajemy liczbę $e$, którą magicznie nazywa się podstawą logarytmu naturalnego.

$$e\approx 2.718\ldots$$

Nazwa dobrana jest świetnie, niestety nikt nie tłumaczy dlaczego tak właściwie jest. Cała sprawa jest niezwykle ciekawa, jej wyjaśnienie to temat nowej serii artykułów „o liczbie e”. Tym samym wzbogacam cykl „dlaczego?”. Dowody przeprowadzę „metodą elementarną” – wszak chodzi o „pierwotność / naturalność” $e$. Będzie kilka dużych „odcinków” – zapraszam 🙂

Nota historyczna

Liczba e pojawia się w wielu dziedzinach. W matematyce jest wszechobecna! Z powodzeniem dorównuje liczbie $\pi$. Analiza matematyczna (w szczególności rachunek różniczkowy i całkowy, równania różniczkowe), funkcje specjalne, analiza zespolona, rachunek prawdopodobieństwa, statystyka matematyczna – to najbardziej wyraziste przykłady. W innych naukach ścisłych (np.: ekonomia, fizyka, biologia) liczba e pojawia się w wielu ważnych równaniach, w tym: równanie przewodnictwa cieplnego, wzór barometryczny, rozpady promieniotwórcze, fazory, funkcja falowa w mechanice kwantowej, wzrost populacji, procent składany.

Pierwsze informacje na temat liczby e pojawiły się w 1618 roku. Opublikował je John Napier, przygotowując tabele logarytmów. Praca nie zawierała samej stałej, prezentowała niektóre wartości logarytmów na bazie e. Liczbę e w jej dzisiejszej postaci odkrył Jacob Bernoulli. Dokonał tego w 1683 roku analizując własności procentu składanego. Pierwsze udokumentowane wykorzystanie liczby e, wtedy oznaczanej przez b, pojawiło się w latach 1690-1691 (Gottfried Leibniz, Christiaan Huygens). Wykorzystanie stałej znacząco rozwinął Leonhard Euler oznaczając ją w 1727 roku do dziś wykorzystywanym symbolem $e$.

Procent składany

Cytując Wikipedię – procent składany (ang. compound interest) to sposób oprocentowania wkładu pieniężnego polegający na tym, że odsetki za dany okres oprocentowania są doliczane do wkładu (podlegają kapitalizacji) i w ten sposób „składają się” na zysk wypracowywany w okresie następnym. Proces kapitalizacji opisuje się odpowiednim ciągiem geometrycznym:

$V_0$ – kapitał początkowy

$r$ – nominalna roczna stopa zwrotu, wyrażona w procentach (r = 0,05 dla 5% rocznej stopy zwrotu)

$k$ – liczba lat

$V_k$ – kapitał końcowy po $k$ latach

Kapitalizacja roczna	$V_k^1=V_0(1+r)^k$
Kapitalizacja półroczna	$V_k^2=V_0\bigg(1+\frac{r}{2}\bigg)^{2k}$
Kapitalizacja kwartalna	$V_k^4=V_0\bigg(1+\frac{r}{4}\bigg)^{4k}$
Kapitalizacja miesięczna	$V_k^{12}=V_0\bigg(1+\frac{r}{12}\bigg)^{12k}$
Kapitalizacja $n$-krotna	$V_k^{n-krotna}=V_0\bigg(1+\frac{r}{n}\bigg)^{nk}$

Oczywiście im częstsza kapitalizacja tym większy kapitał końcowy.

Naturalny wzrost

Rozważmy sytuację, gdy kapitał początkowy $V_0=1$ oraz roczna stopa zwrotu to 100%, tzn $r=1$. Załóżmy ponadto, że inwestycja potrwa $1$ rok. Innymi słowy – startujemy z $1$, przez okres $1$ powiększamy o $r=1$, mierzymy kapitał końcowy dla różnych częstotliwości kapitalizacji.

$$V_1^n=\bigg(1+\frac{1}{n}\bigg)^n$$

Poniżej różne warianty kapitalizacji + reprezentacja graficzna w czasie.

Kapitalizacja roczna	$V_1^1=\bigg(1+\frac{1}{1}\bigg)^1=2$
Kapitalizacja półroczna	$V_1^2=\bigg(1+\frac{1}{2}\bigg)^2=2.25$
Kapitalizacja kwartalna	$V_1^4=\bigg(1+\frac{1}{4}\bigg)^4\approx 2.441$
Kapitalizacja miesięczna	$V_1^{12}=\bigg(1+\frac{1}{12}\bigg)^{12}\approx 2.613$
Kapitalizacja tygodniowa	$V_1^{52}=\bigg(1+\frac{1}{52}\bigg)^{52}\approx 2.693$
Kapitalizacja dzienna	$V_1^{365}=\bigg(1+\frac{1}{365}\bigg)^{365}\approx 2.715$
Kapitalizacja ciągła	$V_1=\displaystyle\lim_{n\to\infty}\bigg(1+\frac{1}{n}\bigg)^n=e\approx 2.718$

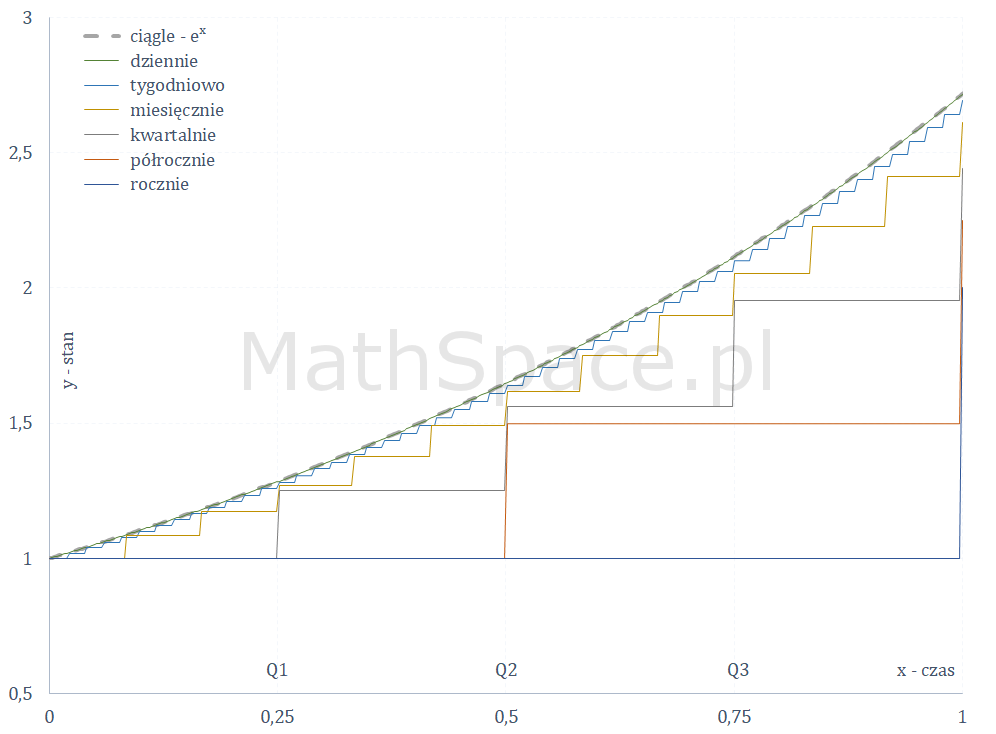
Trudno nie odnieść wrażenia, że wraz ze wzrostem częstości kapitalizacji, krzywa reprezentująca saldo w czasie $x$ „wygładza się” i zbiega do pewnej funkcji. To zaś sugeruje, że taka granica przedstawia naturalne tempo wzrostu przy uwzględnieniu ciągłego czasu kapitalizacji, przy standardowych (naturalnych) warunkach początkowych – stan początkowy $1$, tempo wzrostu $100$% w $1$ okresie czasu. Okazuje się, że funkcja graniczna to

$${\Large e^x}$$

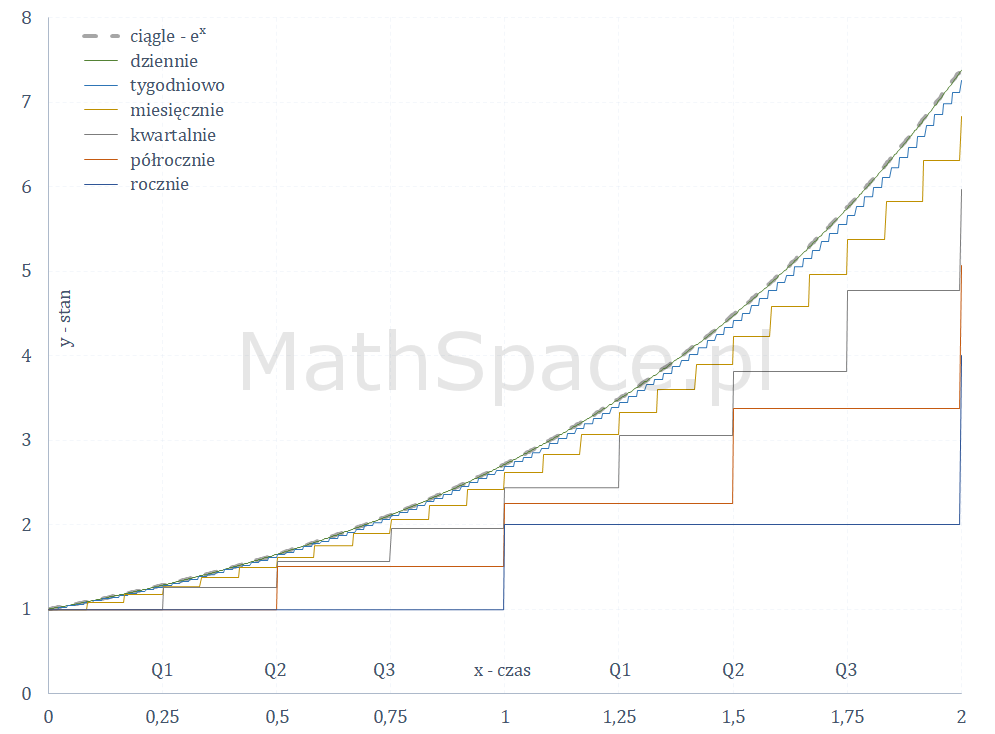
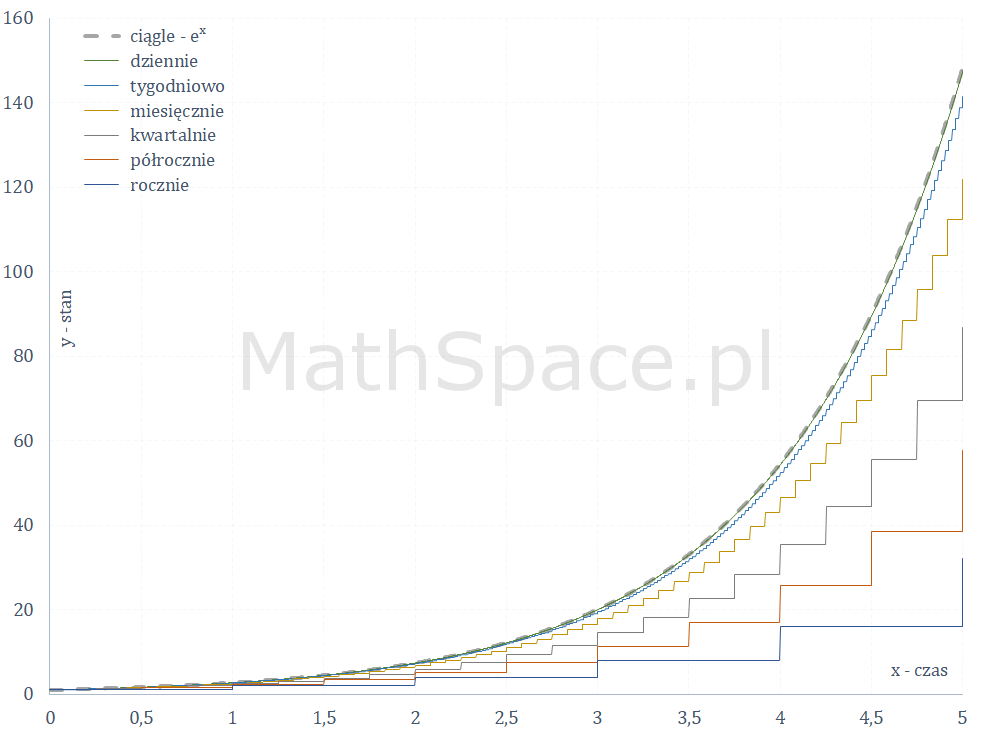
Sytuacja wygląda bardzo podobnie po dodaniu kapitalizacji na kolejne lata.

Definicja liczby $e$

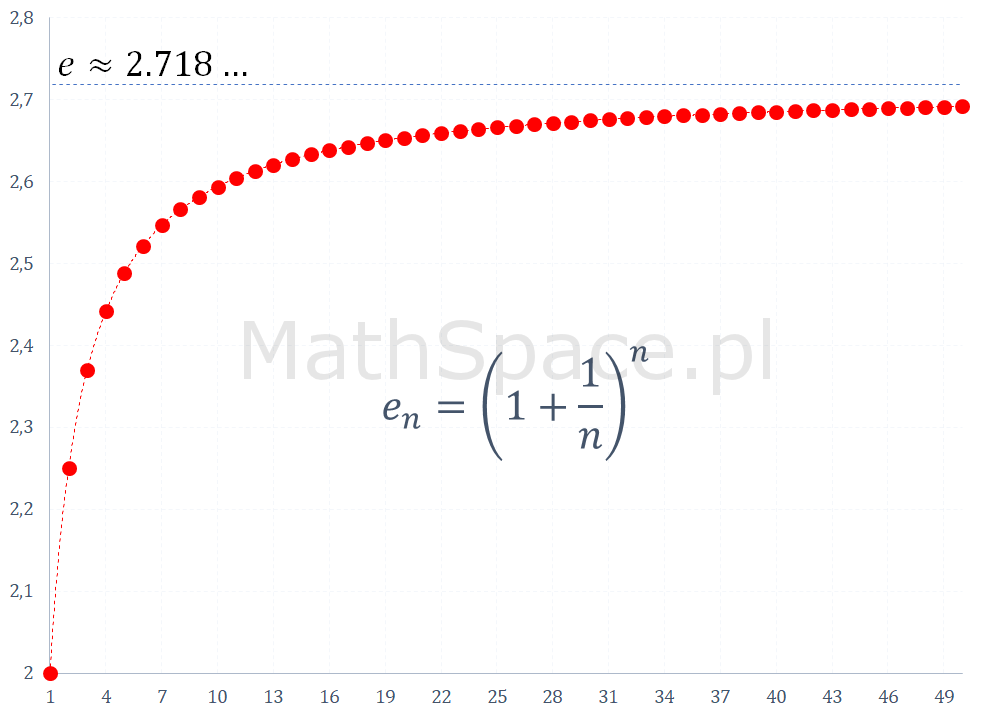
Najczęściej liczbę $e$ definiuje się jako granicę ciągu

$$e=\displaystyle\lim_{n\to\infty}\bigg(1+\frac{1}{n}\bigg)^n$$

Zapiszmy

$$e_n=\bigg(1+\frac{1}{n}\bigg)^n$$

wtedy

$$e=\displaystyle\lim_{n\to\infty}e_n$$

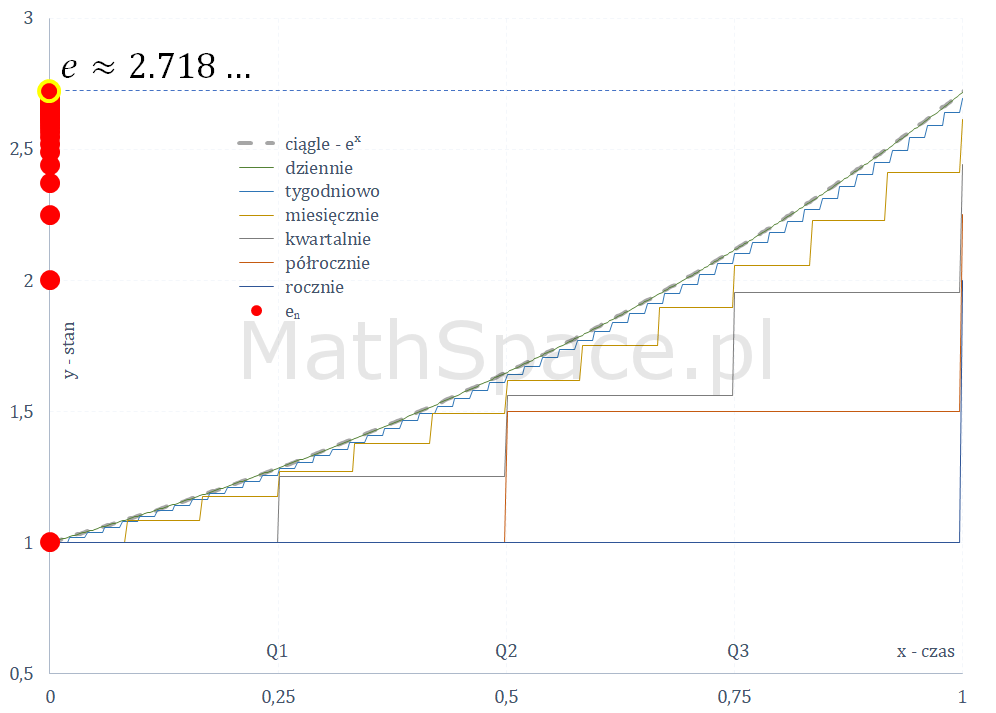
Powyższy wykres sugeruje, że liczba $e$ jest większa od $2.5$ i mniejsza od $3$.

Zbieżność ciągu $e_n=\bigg(1+\frac{1}{n}\bigg)^n$

Wykażemy, że ciąg

$$e_n=\bigg(1+\frac{1}{n}\bigg)^n$$

jest monotoniczny (w tym wypadku rosnący) i ograniczony.

Dowód monotoniczności: $e_{n+1}>e_n$

Korzystając z rozwinięcia w dwumian Newtona zapisujemy

$$e_n=\bigg(1+\frac{1}{n}\bigg)^n=\displaystyle\sum_{k=0}^n{n\choose k}1^{n-k}\bigg(\frac{1}{n}\bigg)^k=$$

$$=\displaystyle\sum_{k=0}^n{n\choose k}\frac{1}{n^k}=\displaystyle\sum_{k=0}^n\frac{n!}{k!(n-k)!}\cdot\frac{1}{n^k}=$$

$$=\displaystyle\sum_{k=0}^n\frac{(n-k)!\Big(n-(k-1)\Big)\ldots\Big(n-(k-k)\Big)}{k!(n-k)!}\cdot\frac{1}{n^k}=$$

$$=\displaystyle\sum_{k=0}^n\frac{1}{k!}\cdot\frac{\Big(n-(k-1)\Big)\ldots\Big(n-(k-k)\Big)}{n^k}=$$

$$=\displaystyle\sum_{k=0}^n\frac{1}{k!}\cdot\frac{n-(k-1)}{n}\ldots\frac{n-(k-k)}{n}=$$

$$=\displaystyle\sum_{k=0}^n\frac{1}{k!}\displaystyle\prod_{i=1}^k\frac{n-(k-i)}{n}=$$

$$=\displaystyle\sum_{k=0}^n\frac{1}{k!}\displaystyle\prod_{i=1}^k\Bigg(1-\frac{k-i}{n}\Bigg)=$$

$$=\displaystyle\sum_{k=0}^n\frac{1}{k!}\displaystyle\prod_{i=1}^{k-1}\Bigg(1-\frac{i}{n}\Bigg)$$

Porównując kolejne wyrazy ciągu $e_n$

$$e_n=\displaystyle\sum_{k=0}^n\frac{1}{k!}\displaystyle\prod_{i=1}^{k-1}\Bigg(1-\frac{i}{n}\Bigg)$$

$$e_{n+1}=\displaystyle\sum_{k=0}^{n+1}\frac{1}{k!}\displaystyle\prod_{i=1}^{k-1}\Bigg(1-\frac{i}{n+1}\Bigg)$$

łatwo zauważyć, że

$$1-\frac{i}{n+1}>1-\frac{i}{n}$$

ponadto $e_{n+1}$ (w stosunku do $e_n$) zawiera jeden dodatkowy element sumy. Tym samy stwierdzamy, że

$$e_{n+1}>e_n$$

Dowód ograniczenia z góry: $e_n<M$

Wyżej pokazaliśmy, że

$$e_n=\displaystyle\sum_{k=0}^n\frac{1}{k!}\cdot\frac{\Big(n-(k-1)\Big)\ldots\Big(n-(k-k)\Big)}{n^k}=$$

$$=1+1+\displaystyle\sum_{k=2}^n\frac{1}{k!}\cdot\frac{\Big(n-(k-1)\Big)\ldots\Big(n-(k-k)\Big)}{n^k}$$

ale dla $k\geq 2$ zachodzi

$$\frac{1}{k!}<\frac{1}{2^{k-1}}$$

co jest konsekwencją

$$k!=\underbrace{2\times 3\times\ldots\times k}_{k-1~el.}>\underbrace{2\times 2\times\ldots\times 2}_{k-1~el.}=2^{k-1}$$

Dodatkowo

$$\frac{\Big(n-(k-1)\Big)\ldots\Big(n-(k-k)\Big)}{n^k}<1$$

gdyż

$$\underbrace{\Big(n-(k-1)\Big)\ldots\Big(n-(k-k)\Big)}_{k~el.}<\underbrace{n\times n\ldots\times n}_{k~el.}=n^k$$

zatem

$$e_n<1+1+\displaystyle\sum_{k=2}^n\frac{1}{2^{k-1}}\cdot 1=$$

$$=1+ \underbrace{\displaystyle\sum_{k=1}^n\frac{1}{2^{k-1}}}_{c.~geom.~q=\frac{1}{2}}$$

redukując sumę $n$ pierwszych wyrazów ciągu geometrycznego, gdzie $a_1=1$ oraz $q=\frac{1}{2}$, otrzymujemy

$$e_n<1+\frac{1-\frac{1}{2^n}}{1-\frac{1}{2}}=1+2-\frac{1}{2^{n-1}}=3-\frac{1}{2^{n-1}}<3$$

$$e_n<3$$

Na mocy twierdzenia o zbieżności ciągu monotonicznego i ograniczonego stwierdzamy, że $e_n$ jest zbieżny oraz

$$\displaystyle\lim_{n\to\infty}e_n=\displaystyle\sup_{n\in\mathbb{N}}\Bigg\{\Big(1+\frac{1}{n}\Big)^n\Bigg\}=e\approx 2.718$$

Ciąg dalszy nastąpi … w kolejnej część funkcja wykładnicza $a^x$ i jej pochodna 🙂

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

https://youtu.be/YSOZPiXw6CY

https://youtu.be/XTOjmucEAsw

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa