W 13 części cyklu „Ocena jakości klasyfikacji” przedstawię dodatkowe interpretacje dla krzywej liftu nieskumulowanego i krzywej Captured Response. Obiecuję, że będzie ciekawie 🙂 przecież robimy „deep dive into predictive model assessment curves”. W dzisiejszym odcinku zapomnimy o punktach odcięcia, klasyfikatorach binarnych, rozważając rozkłady populacji jako całość. Chwilkę się do tego przygotowywałem – było warto – seria „Tips & Tricks na krzywych” nabiera rumieńców!

Pole powierzchni pod krzywą liftu nieskumulowanego

Lift nieskumulowany dla modelu losowego to funkcja stała o wartości 1. Pole pod taką krzywą równe jest polu kwadratu o boku 1 i wynosi oczywiście 1. Model losowy „rozrzuca” obserwacje z „klasy 1” równomiernie, tzn. taka sama część otrzymuje wysoki, średni i niski score. Głównym zadaniem modelu predykcyjnego, w pewnym sensie, jest „przepchnąć” obserwacje należące do „klasy 1” z segmentu niskiego score do segmentu wysokiego score – dzięki temu pojawia się separacja klas. Powyższe dobrze obrazuję animacją, gdzie siła modelu utożsamiana jest z „siłą podmuchu wiatru” 🙂

Takie „przepchnięcie” nie ma wpływu na ilość „jedynek”, zatem należy podejrzewać, że pole pod krzywą liftu nieskumulowanego zawsze wynosi 1. No to całkujemy:

$$\displaystyle\int_0^1 Lift.Niesk(q)dq$$

Oznaczenia + zależności:

• $N=N_1+N_0$ – liczba obserwacji: łączna, z „klasy 1”, z „klasy 0”;
• $k$ – liczba przedziałów, na które dzielimy odcinek $[0;1]$;
• $p=\frac{1}{k}$ – szerokość pojedynczego przedziału (zakres zmienności rzędu kwantyli);
• $p\cdot N$ – liczba obserwacji w przedziale (podział po kwantylach, zatem po równo);
• $i=\{1,2,3,\ldots,k\}$ – numer przedziału;
• $n_1^i+n_0^i=pN$ – liczba obserwacji w przedziale, osobno „z klasy 1” i „z klasy 0”;
• $\Delta q^i$ – przedział, na którym wyznaczona jest wartość liftu nieskumulowanego;
• $\displaystyle\sum_{i=1}^k n_1^i=N_1$
• $\displaystyle\sum_{i=1}^k n_0^i=N_0$
• $\displaystyle\sum_{i=1}^k n_1^i+n_0^i=N_1+N_0=N$

Lift nieskumulowany jest funkcją przedziałami stałą:

$$Lift.Niesk(q)=Lift.Niesk(\Delta q^i)\quad\text{dla}\quad q\in\Delta q^i$$

$$Lift.Niesk(\Delta q^i)=\frac{P(1|\Delta q^i)}{P(1)}$$

$$P(1|\Delta q^i)=\frac{n_1^i}{pN}$$ oraz $$P(1)=\frac{N_1}{N}$$

$$Lift.Niesk(\Delta q^i)=\frac{n_1^i}{pN}\cdot \frac{N}{N_1}=\frac{n_1^i}{pN_1}$$

$$Lift.Niesk(\Delta q^i)=\frac{n_1^i}{pN_1}$$

$$\displaystyle\int_0^1 Lift.Niesk(q)dq=\displaystyle\sum_{i=1}^k p\cdot Lift.Niesk(\Delta q^i)$$

$$\displaystyle\sum_{i=1}^k p\cdot Lift.Niesk(\Delta q^i)=\displaystyle\sum_{i=1}^k p\frac{n_1^i}{pN_1}=$$

$$=\displaystyle\sum_{i=1}^k \frac{n_1^i}{N_1}=\frac{\displaystyle\sum_{i=1}^k n_1^i}{N_1}=\frac{N_1}{N_1}=1$$

$$\displaystyle\int_0^1 Lift.Niesk(q)dq=1$$

Lift nieskumulowany jako funkcja gęstości rozkładu prawdopodobieństwa

Funkcja liftu nieskumulowanego jest nieujemna i spełnia warunek „unormowania” (w przeciwieństwie do funkcji nieskumulowanego prawdopodobieństwa) w kontekście gęstości rozkładu prawdopodobieństwa – tzn. pole powierzchni pod krzywą wynosi 1. Taka gęstość opisuje rozkład rzędu kwantyli (kwantyle wyznaczane dla całej populacji „klasa 0 + klasa 1” względem malejącej oceny modelem) w klasie faktycznie pozytywnej – tzn. w „klasie 1”.

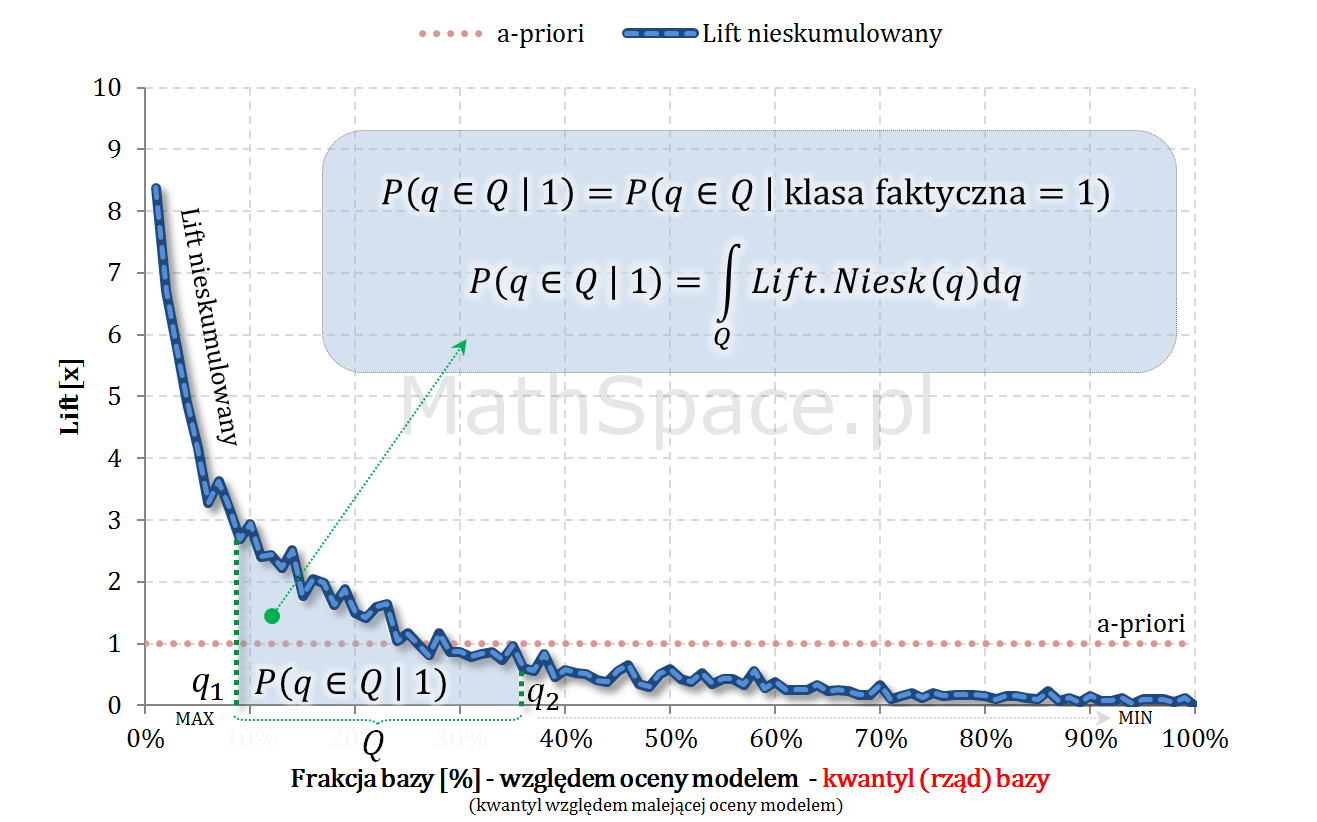
Jeśli

$$Q=(q_1,q_2)$$

to

$$P(q\in Q|1)=\displaystyle\int_{q_1}^{q_2}Lift.Niesk(q)dq$$

Captured Response jako dystrybuanta rozkładu prawdopodobieństwa

Captured Response jest funkcją niemalejącą, jednostronnie ciągłą (powiedzmy, że prawostronnie), o wartościach z przedziału $[0;1]$, wartości 0 dla $q\leq 0$ oraz wartości 1 dla $q\geq 1$. Tym samym spełnione są warunki bycia dystrybuantą pewnego rozkładu prawdopodobieństwa. W części „#11 – Captured Response vs Lift” wykazałem, że pochodna z Captured Response to lift nieskumulowany. Wniosek: Captured Response i lift nieskumulowany to dystrybuanta i gęstość tego samego rozkładu prawdopodobieństwa.

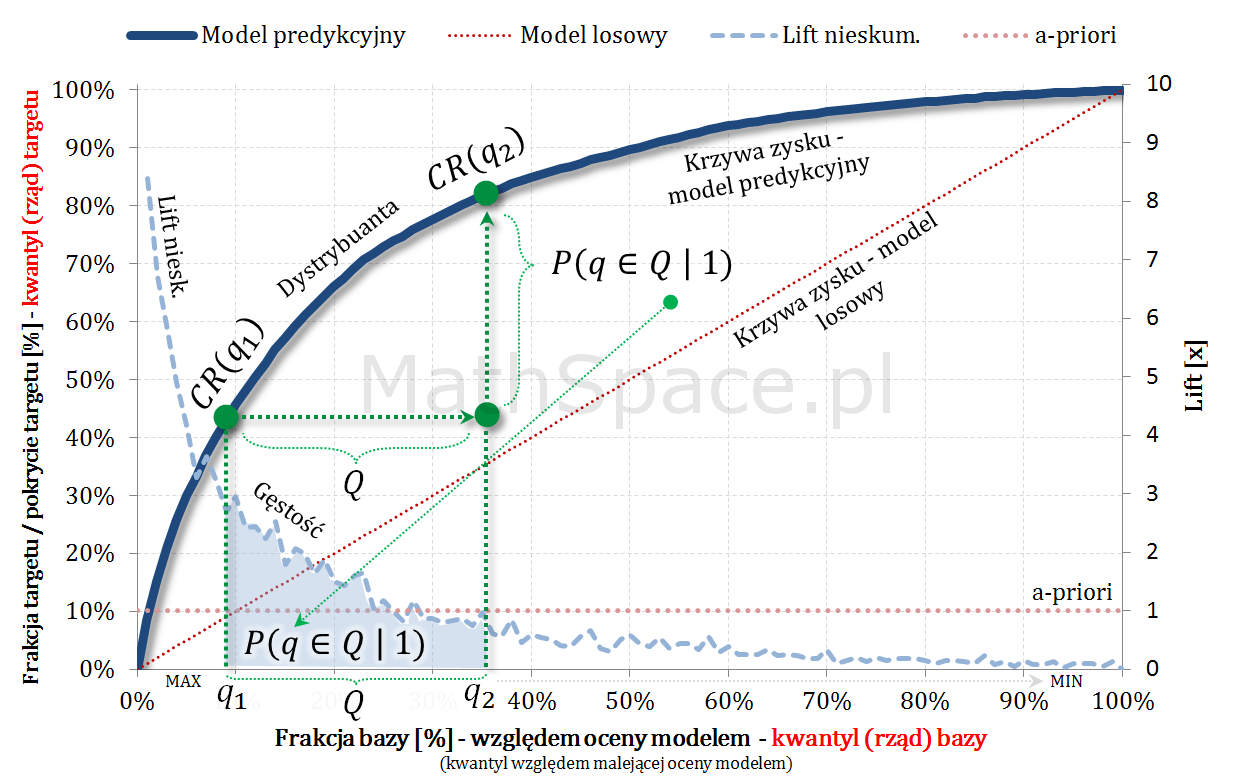
Jeśli

$$Q=(q_1,q_2)$$

to

$$P(q\in Q|1)=\displaystyle\int_{q_1}^{q_2}Lift.Niesk(q)dq=CR(q_2)-CR(q_1)$$

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa