„Plaża, piękna pogoda, sielanka i relaks! Różne funkcje wypoczywają. Nagle … popłoch, panika! Funkcje uciekają. Tylko jedna nadal się opala.
– Co robisz? Uciekaj! Nadchodzi operator różniczkowy!
– Nie boję się, jestem $e^x$.
I tak spokojna $e^x$ została. Wpada operator.
– Wrrr! Teraz Cię zróżniczkuję! Wrrr!
– A proszę bardzo – jestem $e^x$ – nic mi nie grozi.
– Kochana, ja różniczkuję po $dy$”
Ten iście „nerdowski” dowcip całkiem dobrze rozpoczyna kolejną część serii „o liczbie e”. Na bazie pochodnej przedstawię dodatkowe argumenty „dlaczego?” liczba e jest tak naturalna. Zaczynamy od powtórki podstaw w zakresie potęgowania. Prawdopodobnie zaskoczę Cię już samą definicją funkcji wykładniczej $a^x$ 🙂
Definicja funkcji wykładniczej na bazie potęgowania
Funkcję $f:\mathbb{R}\to\mathbb{R}$ daną wzorem
$f(x)=a^x$ dla $a>0$
nazywamy funkcją wykładniczą.
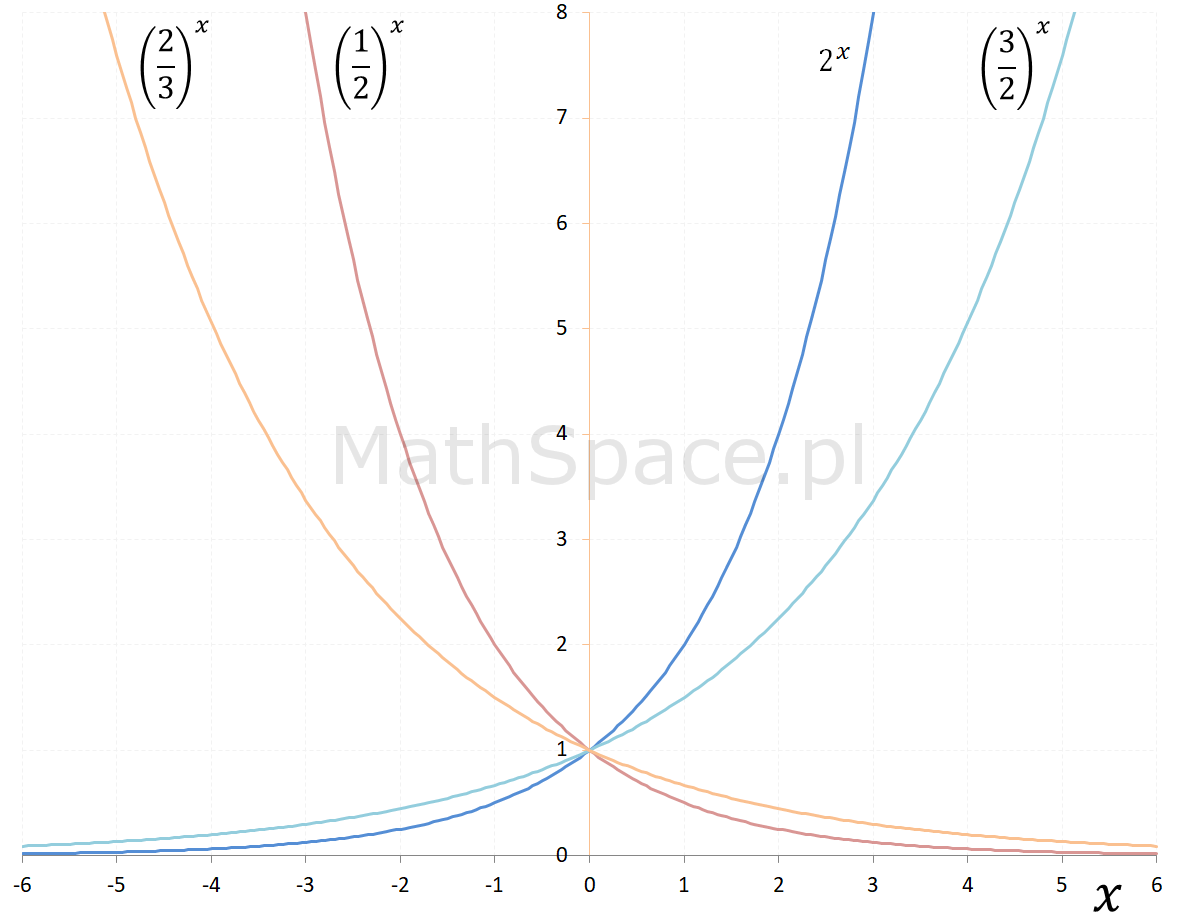
O ile potęgowanie z wykładnikiem naturalnym nie sprawia problemu, to już uogólnienie na liczby wymierne i rzeczywiste nie jest wcale trywialne. Poniżej tabela „przejścia” od potęgowania do funkcji wykładniczej.
| $a$ – zakres | $x$ – zakres | $a^x$ – definicja |
| $a=0$ | $x=0$ | $a^x=0^0=\text{symb. nieokr.}$ |
| $a=0$ | $x>0$ | $a^x=0^x=0$ |
| $a\neq 0$ | $x=0$ | $a^x=a^0=1$ |
| $a\in\mathbb{R}$ | $x=1$ | $a^x=a^1=a$ |
| $a\in\mathbb{R}$ | $x=n\in\mathbb{N}$ | $a^x=a^n=\underbrace{a\times a\times\ldots\times a}_{n}$ |
| $a>0$ | $x=\frac{1}{n}$; $n\in\mathbb{N}$ | $a^x=a^\frac{1}{n}=\sqrt[n]{a}$ |
| $a>0$ | $x=\frac{m}{n}$; $m,n\in\mathbb{N}$ | $a^x=a^\frac{m}{n}=$ $\underbrace{a^\frac{1}{n}\times a^\frac{1}{n}\times\ldots\times a^\frac{1}{n}}_{m}=$ $\underbrace{\sqrt[n]{a}\times \sqrt[n]{a}\times\ldots\times\sqrt[n]{a}}_{m}=\sqrt[n]{a^m}$ |
| $a>0$ | $x>0$ | $a^x=\displaystyle\lim_{r\to x,~r\in\mathbb{Q}}a^r=\displaystyle\sup_{r\in\mathbb{Q},~ r<x}\{a^r\}$ |
| istnieje $a^x\neq 0$ | $a^{-x}=\frac{1}{a^x}$ |
Funkcja wykładnicza ma wiele ciekawych własności, skupię się na najważniejszych. Nie zamieszczam dowodów (są obszerne, raczej nietrudne), zainteresowanych odsyłam do: link 1, link 2, link 3, link 4.
| Suma wykładników | $a^{x+y}=a^x\cdot a^y$ |
| Różnica wykładników | $a^{x-y}=\frac{a^x}{a^y}$ |
| Iloczyn wykładników | $a^{x\cdot y}=\big(a^x\big)^y$ |
| Iloczyn podstaw | $(ab)^x=a^x\cdot b^x$ |
| Iloraz podstaw | $\Big(\frac{a}{b}\Big)^x=\frac{a^x}{b^x}$ |
| Ciągłość | $a^x=\displaystyle\lim_{y\to x}a^y$ |
| Monotoniczność, rosnąca dla $a>1$ | $x>y\Rightarrow a^x>a^y$ |
| Monotoniczność, malejąca dla $0<a<1$ | $x>y\Rightarrow a^x<a^y$ |
| Różniczkowalność, nieskończenie wiele razy | $\displaystyle\forall_{x\in\mathbb{R}}~\displaystyle\forall_{n\in\mathbb{N}}$ istnieje $\frac{\text{d}}{\text{d}x^n}a^x$ |
Twierdzenie: funkcję wykładniczą $a^x$ jednoznacznie definiuje następujące równanie funkcyjne, przy założeniu, że $a>0$ oraz $f:\mathbb{R}\to\mathbb{R}$ jest funkcją ciągłą przynajmniej w jednym punkcie
$$(1)~~~\begin{cases}f(x+y)=f(x)\cdot f(y)\\f(1)=a\end{cases}$$
Szkic dowodu:
„$f(x)=a^x\Longrightarrow(1)$”: wynika z własności funkcji wykładniczej.
„$f(x)=a^x\Longleftarrow(1)$”: szkic dowodu w kilku krokach
Własność 1: $f(x)\neq 0$
$$a=f(1)=f(x+1-x)=$$
$$=f(x)\cdot f(1-x)\neq 0$$
$$f(x)\neq 0$$
$$f(1-x)\neq 0$$
Własność 2: $f(x)>0$
$$f(x)=f(\frac{x}{2}+\frac{x}{2})=$$
$$=f(\frac{x}{2})\cdot f(\frac{x}{2})=\Big(f(\frac{x}{2})\Big)^2>0$$
Własność 3: $f(0)=1$
$$f(x)=f(x+0)=f(x)\cdot f(0)$$
$$f(0)=\frac{f(x)}{f(x)}=1$$
Własność 4: $f(-x)=\frac{1}{f(x)}$
$$f(0)=f(x-x)=f(x)\cdot f(-x)=1$$
$$f(-x)=\frac{1}{f(x)}$$
Własność 5: $f$ jest ciągła w $\mathbb{R}$
Niech $y\in\mathbb{R}$ będzie znanym jednym punktem ciągłości $f$, zbadajmy ciągłość $f$ w dowolnym $x\in\mathbb{R}$
$$f(x+\delta)-f(x)=$$
$$=f(x-y+\delta+y)-f(x-y+y)=$$
$$=f(x-y)\cdot f(y+\delta)-f(x-y)\cdot f(y)=$$
$$=f(x-y)\cdot\Big(f(y+\delta)-f(y)\Big)$$
$$\underbrace{f(x-y)\cdot\underbrace{\Big(f(y+\underbrace{\delta}_{\text{gdy}~\delta\to 0})-f(y)\Big)}_{\to 0~\text{bo}~y~\text{to p.c.}~f}}_{\text{z pow.}\to 0}=$$
$$=\underbrace{f(x+\underbrace{\delta}_{\text{gdy}~\delta\to 0})-f(x)}_{\text{w efek.}\to 0~\Rightarrow f~\text{ciag.}}$$
Własność 6: $n\in\mathbb{N}\Rightarrow f(n)=a^n$
$$f(n)=f(\underbrace{1+1+\ldots+1}_{n})=$$
$$=\underbrace{f(1)\cdot f(1)\cdot\ldots\cdot f(1)}_{n}=a^n$$
Własność 7: $n\in\mathbb{N}\Rightarrow f(\frac{1}{n})=\sqrt[n]{a}$
$$a=f(1)=f(\underbrace{\frac{1}{n}+\frac{1}{n}+\ldots\frac{1}{n}}_{n})=$$
$$=\underbrace{f(\frac{1}{n})\cdot f(\frac{1}{n})\cdot\ldots\cdot f(\frac{1}{n})}_{n}$$
$$a=\Big(f(\frac{1}{n})\Big)^n$$
$$f(\frac{1}{n})=\sqrt[n]{a}$$
Własność 8: $m,n\in\mathbb{N}\Rightarrow f(\frac{m}{n})=\sqrt[n]{a^m}$
$$f(\frac{m}{n})=f(\underbrace{\frac{1}{n}+\frac{1}{n}+\ldots\frac{1}{n}}_{m})=$$
$$=\underbrace{f(\frac{1}{n})\cdot f(\frac{1}{n})\cdot\ldots\cdot f(\frac{1}{n})}_{m}=$$
$$=\big(\sqrt[n]{a}\big)^m=\sqrt[n]{a^m}$$
Własność 9: $x\in\mathbb{R}\setminus\mathbb{Q}\Rightarrow f(x)=a^x$
Wynika z ciągłości $f$ i definicji $a^x$ dla niewymiernych $x$.
Podsumowanie: niesamowite, w zasadzie z jednej własności wynika jednoznaczna postać funkcji wykładniczej.
Ciekawostka: rezygnując z warunku na ciągłość $f$ możliwe jest podanie funkcji innej niż wykładnicza, która spełnia warunek $(1)$ – zainteresowanych zapraszam do tego artykułu.
O przyroście wykładniczym
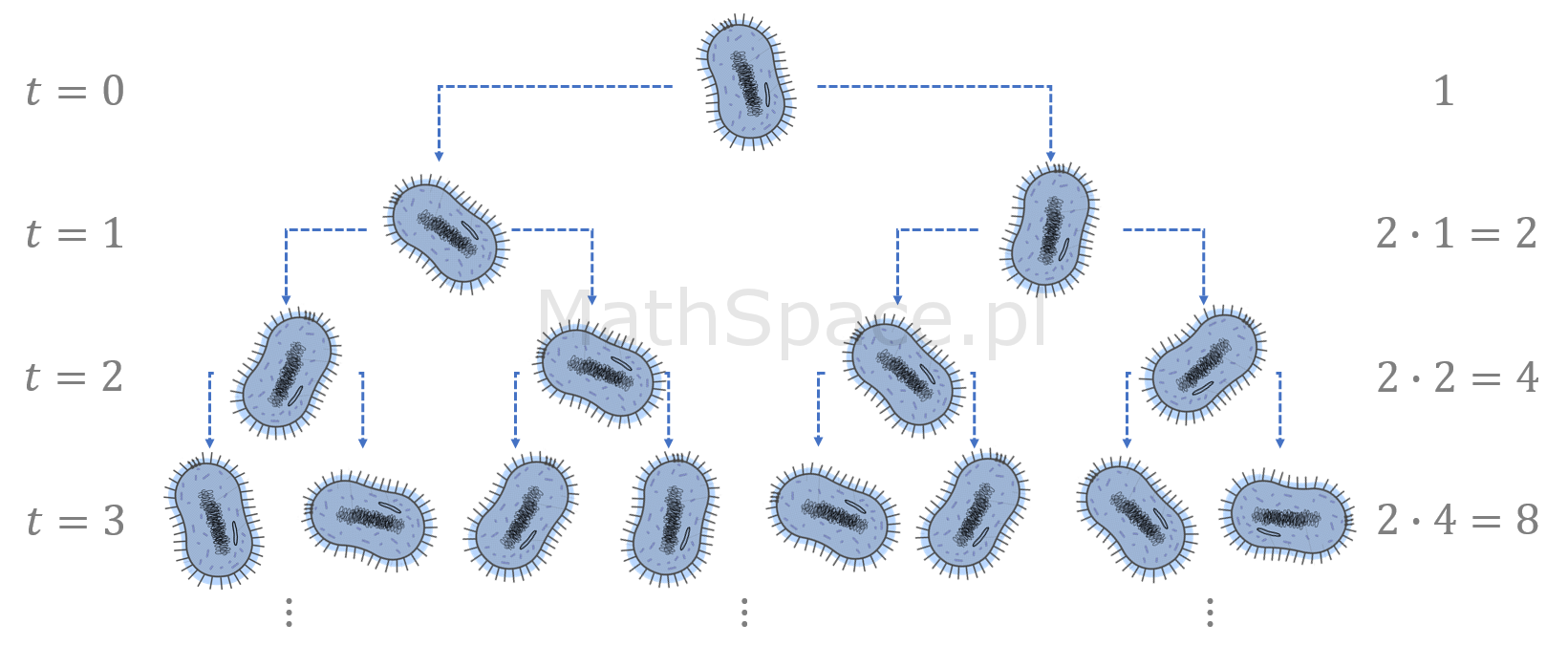O wzroście wykładniczym mówimy, gdy tempo zmiany pewnej wartości (na jednostkę czasu lub w sposób ciągły), jest proporcjonalne do bieżącego stanu. Np. wzrost populacji bakterii – im więcej bakterii, tym szybciej dochodzi do rozmnażania się, a tempo rozmnażania jest proporcjonalne do bieżącej liczby organizmów.
Oznaczając
$t$ – zmienna czasu
$x(t)$ – wartość / stan w czasie $t$ (np. liczba organizmów, masa organizmów)
$x_0=x(0)$ – inicjalny stan układu w czasie $t=0$
$a$ – współczynnik zmiany (wzrostu / spadku) układu w czasie $\tau$
$\tau$ – czas charakterystyczny, w którym układ wzrasta $a$-krotnie
dynamikę wzrostu można zapisać rekurencyjnie
$$x(t+\tau)=a\cdot x(t)$$
W przypadku dyskretnego czasu mamy do czynienia ze wzrostem geometrycznym.
$$x(0)=x_0$$
$$x(\tau)=x(0+\tau)=a\cdot x(0)=x_0\cdot a$$
$$x(2\tau)=x(\tau+\tau)=a\cdot x(\tau)=x_0\cdot a^2$$
$$\ldots$$
$$x(n\tau)=x_0\cdot a^n$$
W przypadku czasu ciągłego wzrost opisywany jest funkcją wykładniczą
$$x(t)=x_0\cdot a^\frac{t}{\tau}$$
Funkcja spełnia zależność rekurencyjną
$$x(t+\tau)=x_0\cdot a^\frac{t+\tau}{\tau}=x_0\cdot a^\frac{t}{\tau}\cdot a^\frac{\tau}{\tau}=a\cdot x(t)$$
oraz dobrze uogólnia przypadek czasu dyskretnego
$$x(n\tau)=x_0\cdot a^\frac{n\tau}{\tau}=x_0\cdot a^n$$
Dla $x_0=1$, $a=2$ oraz $\tau=1$ otrzymujemy chyba „najprostszy” wzrost wykładniczy
$x(t)=2^t$
opisujący np. proces rozmnażania bakterii przez podział.
- Czas dyskretny: proces rozmnażania się organizmów rozumiany jako aktualny stan (liczność) populacji.
- Czas ciągły: proces rozmnażania się organizmów, rozumiany jako aktualna masa populacji.
Naturalny wzrost jako $e^t$
W poprzedniej części „o procencie składanym” podawałem poniższe formuły
Kapitał początkowy 1, 100% stopa zwrotu, kapitał końcowy po 1 roku, n-krotna kapitalizacja:
$$V_1^n=\bigg(1+\frac{1}{n}\bigg)^n$$
Kapitał początkowy 1, 100% stopa zwrotu, kapitał końcowy po k-latach, n-krotna kapitalizacja
$$V_k^n=\bigg(1+\frac{1}{n}\bigg)^{nk}$$
Zdefiniowaliśmy też liczbę $e$ jako
$$e=\displaystyle\lim_{n\to\infty}\bigg(1+\frac{1}{n}\bigg)^n\approx 2.718$$
reprezentującą kapitał po 1 roku przy „ciągłej” kapitalizacji.
Rozważmy kapitał po każdej kolejnej kapitalizacji
| numer kapitalizacji $m$ | czas $t$ | kapitał $V_t^n$ |
| $m=0$, stan pocz. | $t=0$ | $V_t^n=1$ |
| $m=1$ | $t=\frac{1}{n}$ | $V_t^n=1+\frac{1}{n}$ |
| $m=2$ | $t=\frac{2}{n}$ | $V_t^n=\big(1+\frac{1}{n}\big)^2$ |
| … | … | … |
| $m$ | $t=\frac{m}{n}$ | $V_t^n=\big(1+\frac{1}{n}\big)^m$ |
$$t=\frac{m}{n}\Rightarrow m=n\cdot t$$
$$V_t^n=\big(1+\frac{1}{n}\big)^m=\big(1+\frac{1}{n}\big)^{n\cdot t}$$
$$V_t^n=\Bigg(\big(1+\frac{1}{n}\big)^n\Bigg)^t$$
Przy ciągłej kapitalizacji
$$V_t=\displaystyle\lim_{n\to\infty}V_t^n=\displaystyle\lim_{n\to\infty}\Bigg(\bigg(1+\frac{1}{n}\bigg)^n\Bigg)^t=$$
$$=\Bigg(\displaystyle\lim_{n\to\infty}\bigg(1+\frac{1}{n}\bigg)^n\Bigg)^t=e^t$$
$$V_t=e^t$$
Zatem „wzrost naturalny”, opisany mechaniką „procentu składanego”, to przyrost wykładniczy o współczynniku wzrostu $a=e$, czasie charakterystycznym $\tau=1$ oraz inicjalnym stanie $x_0=1$.
Pochodna funkcji wykładniczej
Jeśli $y=a^x$ to, przy ustalonym małym $\Delta x$, przyrost $y$ wynosi
$$\Delta y=a^{x+\Delta x}-a^x=a^x\cdot a^{\Delta x}-a^x$$
$$\Delta y=a^x\cdot (\underbrace{a^{\Delta x}-1}_{\text{const.}})$$
Wtedy możemy podać aproksymację pochodnej
$$\frac{dy}{dx}\approx\frac{\Delta y}{\Delta x}=a^x\cdot\underbrace{\frac{a^{\Delta x}-1}{\Delta x}}_{\text{const.}}$$
Powyższe to przesłanka, że pochodna funkcji wykładniczej jest proporcjonalna do jej samej, ze współczynnikiem
$$\displaystyle\lim_{\Delta x\to 0}\frac{a^{\Delta x}-1}{\Delta x}$$
Jest to efekt oczekiwany, im większa populacja, tym większy potencjał do wzrostu.
Sprawdzamy dla $\Delta x=0.01$
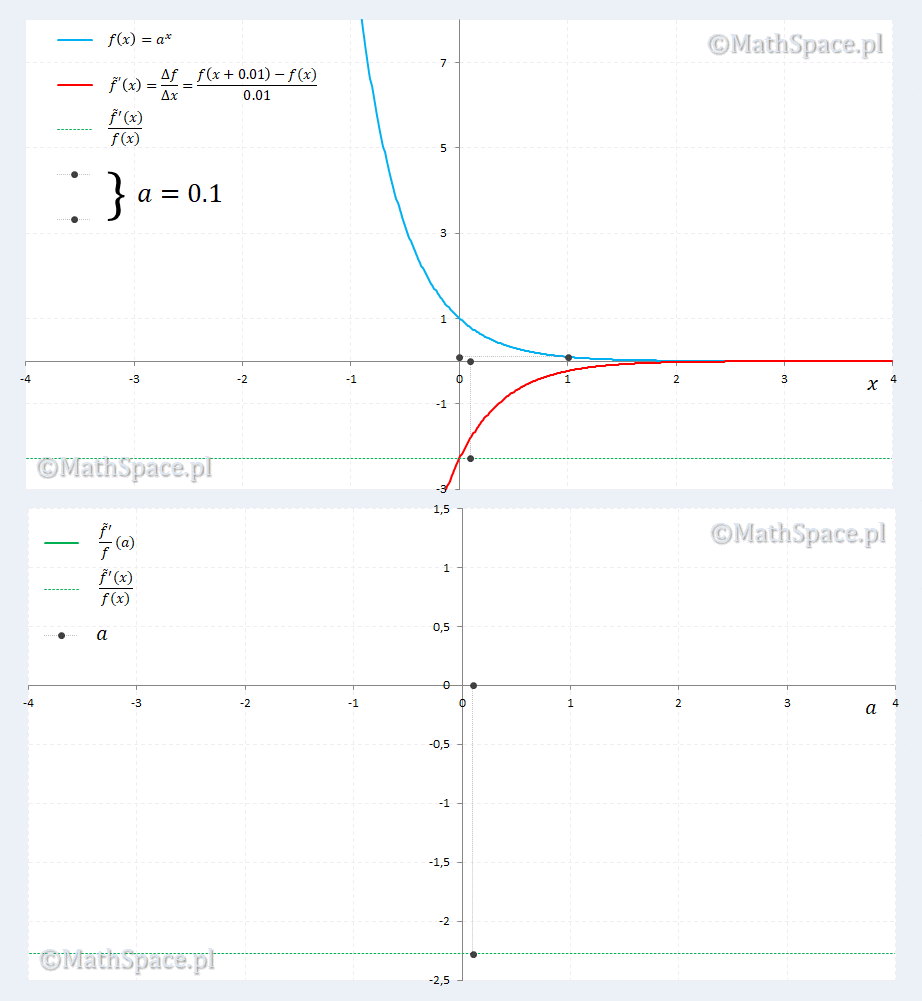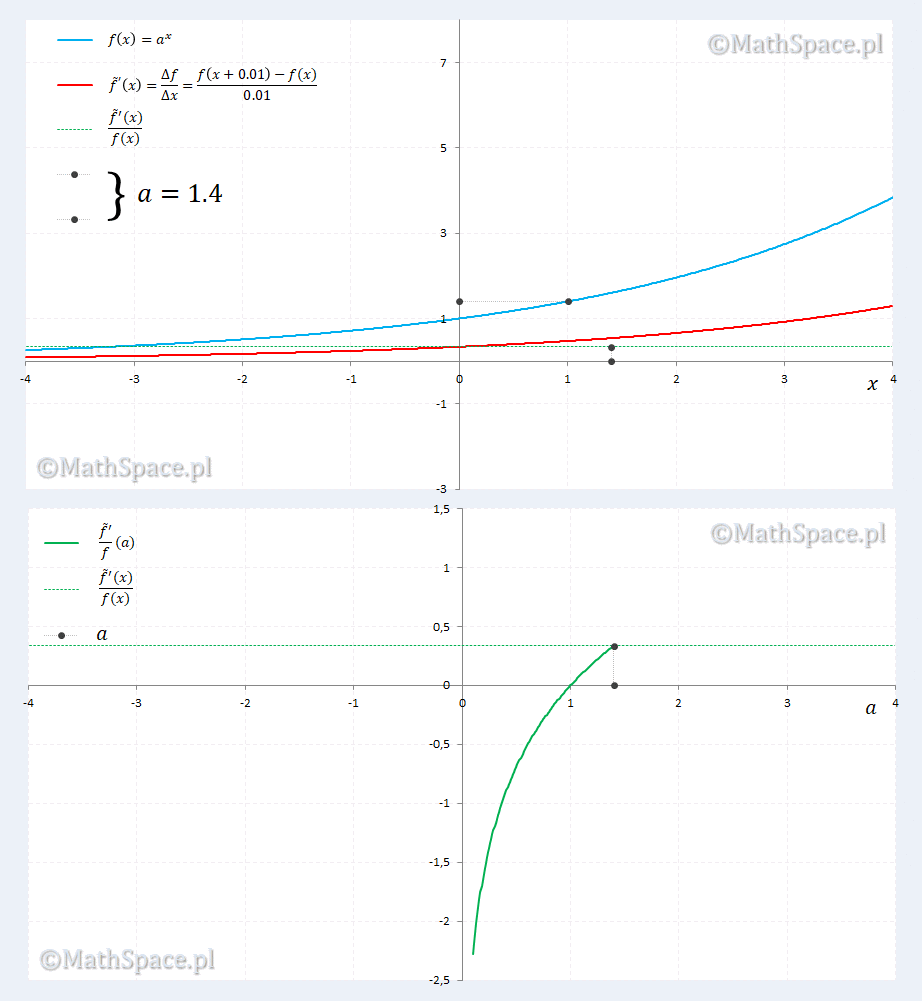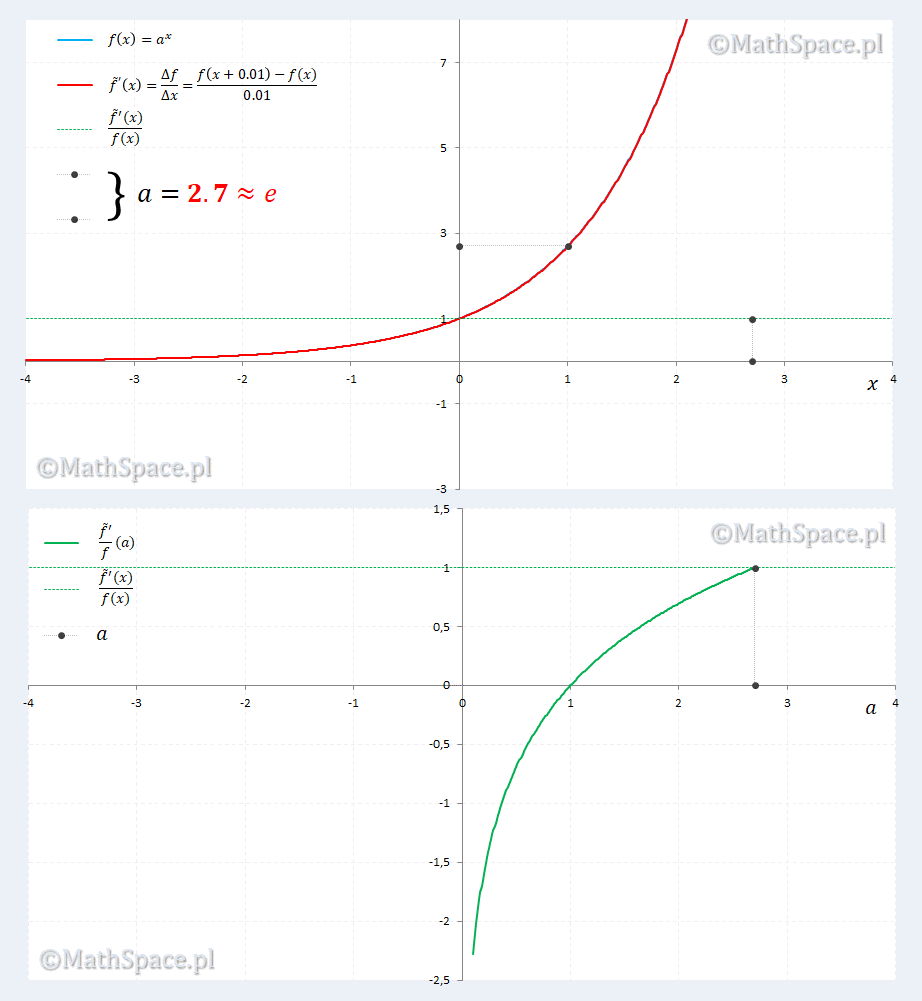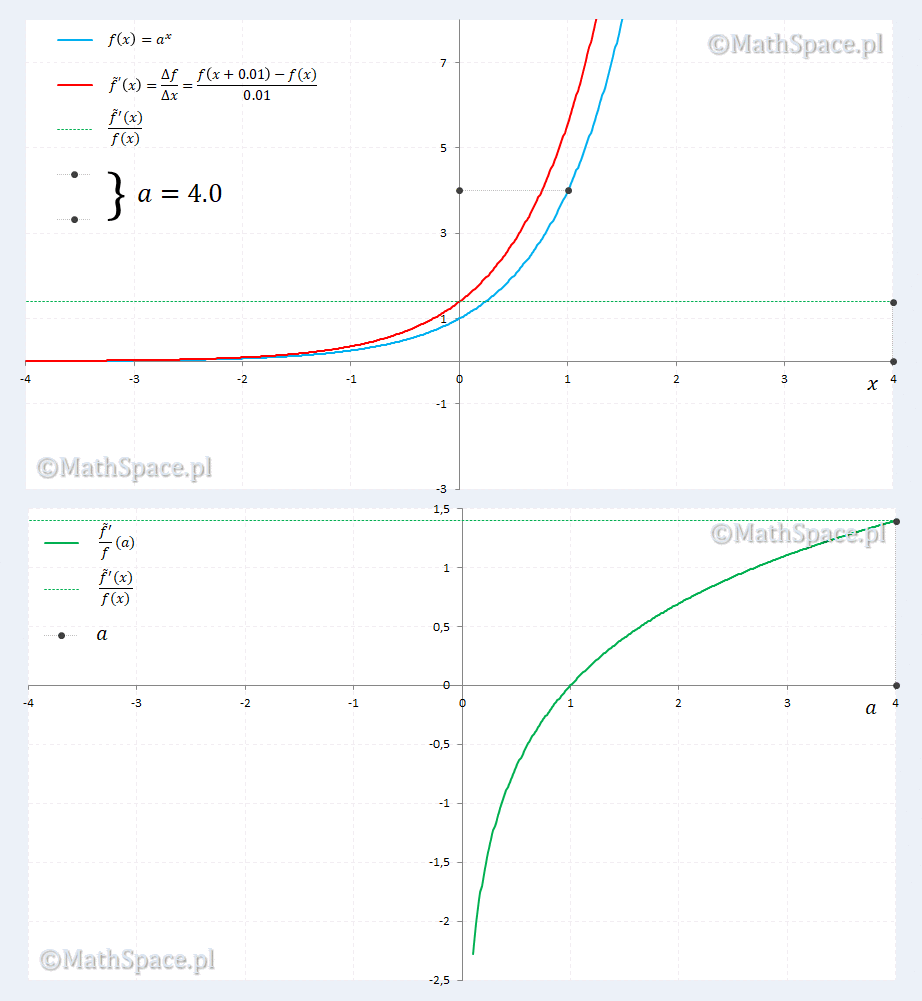
Animacja zdaje się potwierdzać nasze podejrzenia. Ponadto ujawnia się ciekawostka dla $a=2.7\approx=e$, gdzie pokrywają się $a^x$ i pochodna $a^x$. Ciekawostka sprowadza się do rozwiązania równania względem $a$
$$\displaystyle\lim_{\Delta x\to 0}\frac{a^{\Delta x}-1}{\Delta x}=1$$
Pójdziemy nieco na skróty – zakładając, że pochodne istnieją (czyli granice istnieją) oraz, że odpowiednie funkcje są odwracalne. Poniższy dowód nie ma pełni rygoru ścisłości, świetnie natomiast obrazuje zależności.
$$\frac{a^{\Delta x}-1}{\Delta x}\approx 1$$
$$a^{\Delta x}-1\approx\Delta x$$
$$a^{\Delta x}\approx 1+\Delta x$$
$$a\approx\bigg(1+\Delta x\bigg)^\frac{1}{\Delta x}$$
$$a=\displaystyle\lim_{\Delta x\to 0}\bigg(1+\Delta x\bigg)^\frac{1}{\Delta x}$$
Podstawiając
$$\Delta x = \frac{1}{n}$$
$$\Delta x\to 0\Rightarrow n\to\infty$$
$$a=\displaystyle\lim_{n\to\infty}\bigg(1+\frac{1}{n}\bigg)^n=e$$
Wniosek
$$\frac{d}{dx}e^x=e^x$$
$e^x$ to jedyna funkcja, różna od stałej „0”, która posiada tę własność. Tempo wzrostu opisywanego liczbą $e$ zależy wyłącznie od stanu układu w danym czasie i jest bezpośrednio jemu równe. To kolejny argument pokazujący „dlaczego liczba e jest tak naturalna”.
W następnym artykule przedstawię funkcję $\frac{1}{x}$ z interpretacją czasu – czyli będzie o logarytmach (patrz animacja i rysująca się „zielona” krzywa), całkach i pochodnych 🙂
Pozdrowienia,
Mariusz Gromada
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa
