Okres średniowiecza, kobieta winna uprawiania magii, kara straszna – spalenie na stosie! Nadszedł dzień, tłum gawiedzi, czarownica na stosie, płomienie, wiedźma krzyczy – więcej drewna! Więcej drewna! Tłum zdziwiony, mimo wszystko spełnia ostatnie życzenie opętanej. Wiedźma nie przerywa – jeszcze więcej drewna! Więcej drewna! Z oddali dobiega nagły i stanowczy sprzeciw – STOP! Czarownica chce przepełnić stos!
🙂

Czym jest rekurencja?
Zazwyczaj o rekurencji myślimy jako o procesie podziału zadania na mniejsze, następnie podziału na jeszcze mniejsze, i jeszcze mniejsze … dochodząc do zadań, dla których rozwiązanie jest znane. Od tego momentu zaczyna się składanie „mniejszych” rozwiązań w „większe”, następnie tych większych w jeszcze większe, … i w jeszcze większe … kończąc na rozwiązaniu zadania początkowego. Dla przykładu zapiszmy funkcję n! w postaci rekurencyjnej.
$$n!=\begin{cases}n\cdot(n-1)!&\text{dla}\quad n>0\\1,&\text{dla}\quad n=0\end{cases}$$
W celu zobrazowania reprezentacja powyższego podana w mXparser:
/* Definicja funkcji rekurencyjnej */ Function silnia = new Function("s(n) = if( n>0, n*s(n-1), 1 )"); /* Obliczenia i wyświetlenie wyniku */ System.out.println( "n = 0, s(n) = " + silnia.calculate(0) ); System.out.println( "n = 1, s(n) = " + silnia.calculate(1) ); System.out.println( "n = 2, s(n) = " + silnia.calculate(2) ); System.out.println( "n = 3, s(n) = " + silnia.calculate(3) ); System.out.println( "n = 4, s(n) = " + silnia.calculate(4) ); System.out.println( "n = 5, s(n) = " + silnia.calculate(5) );
+ wynik:
n = 0, s(n) = 1.0 n = 1, s(n) = 1.0 n = 2, s(n) = 2.0 n = 3, s(n) = 6.0 n = 4, s(n) = 24.0 n = 5, s(n) = 120.0
Wynik jest zgodny z oczekiwanym. Innym przykład rekurencji to iterowany operator sumowania, niech
$$A_n=a_1+a_2+\ldots+a_n=\sum_{i=1}^n a_i$$
Łatwo zauważyć, że
$$A_n=\begin{cases}a_n+A_{n-1},&\text{dla}\quad n>1\\a_1,&\text{dla}\quad n=1\end{cases}$$
Jak widać, rekurencja jest powszechna, często będąc nieco innym sposobem patrzenia na iteracje.
Formalna definicja rekurencji
O rekurencji mówimy jeśli metoda (funkcja, zachowanie, obiekt) może być opisana przez:
- elementy bazowe / rozwiązania bazowe;
- zestaw reguł, które redukuję (sprowadzają) każdy inny przypadek do (w kierunku) elementów bazowych.
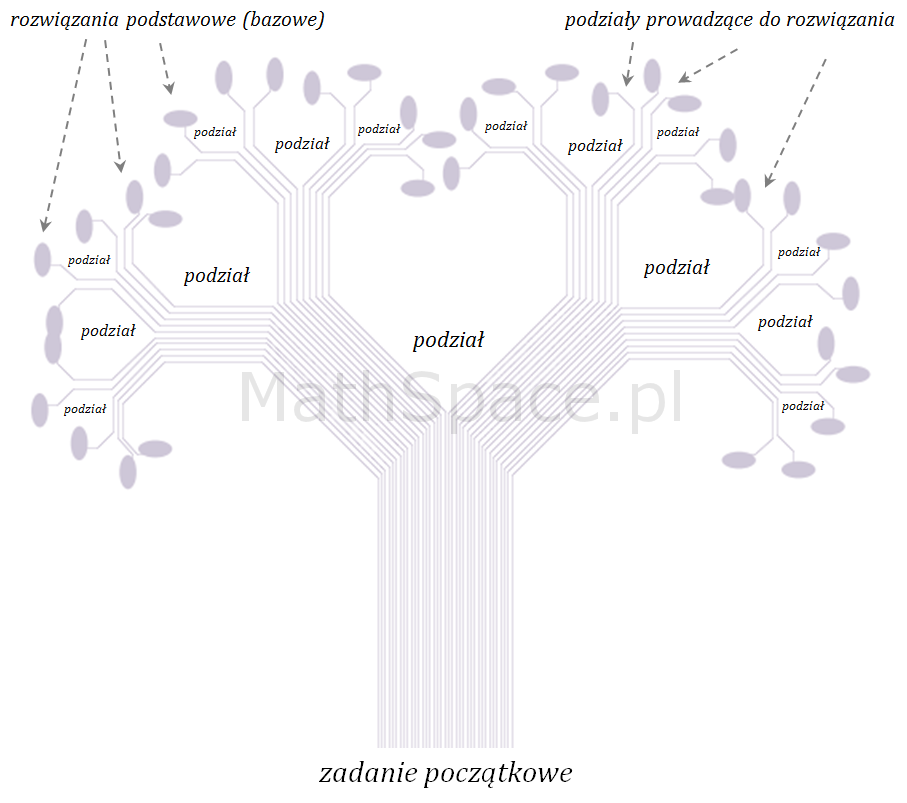
Powyższe określenie jest szerokie, ale takie być musi, bo i typów rekurencji jest wiele.
Rekurencja jako złożenie funkcji
Jednym (ale nie jedynym) sposobem zapisu ogólnych równań rekurencyjnych jest złożenie funkcji:
$$f_n=\begin{cases}F\big(f_{n-1},f_{n-2},\ldots,f_{n-k}\big)&\text{dla}\quad n>k\\f_1,f_2,\ldots,f_k&\text{el. baz. dla}\quad n<=k\end{cases}$$
Dobrą ilustracją powyższego jest ciąg Fibonacciego:
$$f_n=\begin{cases}0&\text{dla}\quad n=0\\1&\text{dla}\quad n=1\\f_{n-1}+f_{n-2}&\text{dla}\quad n>1\end{cases}$$
Zapiszmy ciąg Fibonacciego w mXparser:
/* Definicja funkcji rekurencyjnej */ Function fib = new Function("fib(n) = if( n&amp;gt;1, fib(n-1)+fib(n-2), if(n=1,1,0) )"); /* Obliczenia i wyświetlenie wyniku */ System.out.println( "fib(0) = " + fib.calculate(0) ); System.out.println( "fib(1) = " + fib.calculate(1) ); System.out.println( "fib(2) = " + fib.calculate(2) ); System.out.println( "fib(3) = " + fib.calculate(3) ); System.out.println( "fib(4) = " + fib.calculate(4) ); System.out.println( "fib(5) = " + fib.calculate(5) );
+ rezultat:
fib(0) = 0.0 fib(1) = 1.0 fib(2) = 1.0 fib(3) = 2.0 fib(4) = 3.0 fib(5) = 5.0
Rekurencja w roli pętli „For”
Podane wyżej przykłady zapisów rekurencyjnych (n!, suma n-pierwszych wyrazów ciągu, ciąg Fibonacciego) są tak naprawdę rekurencyjną realizacją pętli „for” – znamy przecież dokładnie liczbę niezbędnych operacji do wykonania, a i same operacje są raczej łatwe oraz czytelne – zatem zagnieżdżenie ich w pętli „for” nie powinno spowodować utraty przejrzystości kodu.
Poszukiwanie rozwiązania – czyli rekurencja w roli pętli „While/Until”
W metodach numerycznych często stosuje się strategie rekurencyjne – w takiej sytuacji, będąc w kroku $n$, weryfikujemy czy propozycja rozwiązania $n$ spełnia kryterium stopu (np. jakość oszacowania), jeśli tak – kończymy z rozwiązaniem $n$, jeśli nie – przechodzimy do badania propozycji rozwiązania $n+1$. Procedurę rozpoczynamy od kroku 0 (zerowego).
Przykład: znając definicję silni chcemy znaleźć pierwsze $n$, dla którego $n! >= 100$ – takie zadanie formalnie możemy zapisać jako:
$$S_n=\begin{cases}S_{n+1},&\text{dla}\quad n!<100\\n,&\text{dla}\quad n!>=100\end{cases}$$
$$n_{100} = S(0)$$
Reprezentacja w mXparser:
/* Definicja funkcji rekurencyjnej */ Function S = new Function("S(n) = if( n! &amp;lt; 100, S(n+1), n )"); /* Obliczenia i wyświetlenie wyniku */ System.out.println( "Pierwsze n, że n! &amp;gt;= 100 to n = " + S.calculate(0) );
+ wynik:
Pierwsze n, że n! &amp;gt;= 100 to n = 5.0
Rekurencja bezpośrednia
Wszystkie omawiane wyżej typy rekurencji polegają na wywołaniu z ciała funkcji „siebie samej”, dlatego należą do bardziej ogólnej klasy nazywanej rekurencją bezpośrednią.
Wydajność
Implementacje na bazie rekurencji są bardzo czytelne, o często minimalnym rozmiarze kodu. Jednak coś za coś – tracimy bardzo dużo na złożoności obliczeniowej (powtarzane operacje, dzielenie zadań, operacje na stosie) oraz wymogach pamięci (głównie struktura stosu) – to właśnie dlatego czarownica błagała o drewno – licząc na przerwanie procesu z tytułu przepełnienia stosu 🙂
Cdn 🙂
Pozdrowienia,
Mariusz Gromada
Zobacz również:
- Prędkość ucieczki do nieskończoności – czyli zabawy z rekurencją (część 2)
- Naiwny test pierwszości – czyli zabawy z rekurencją (część 3)
- Rekurencja pośrednia – czyli zabawy z rekurencją (część 4)
Poza Liczbami: Inne Twórcze Przestrzenie
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury
Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.
