by ·0 Comments

Pole powierzchni figur podobnych zmienia się z kwadratem skali podobieństwa

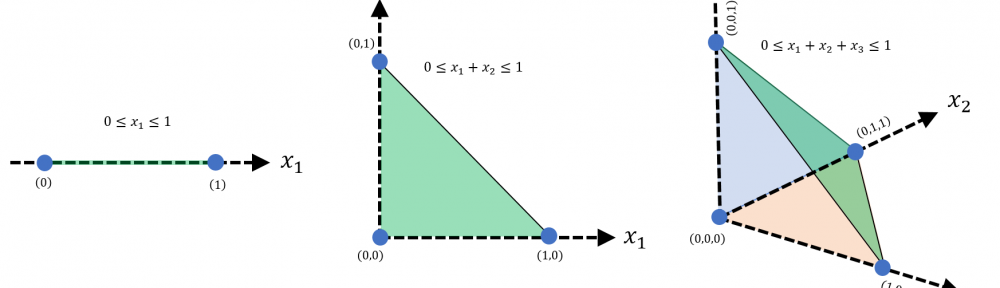
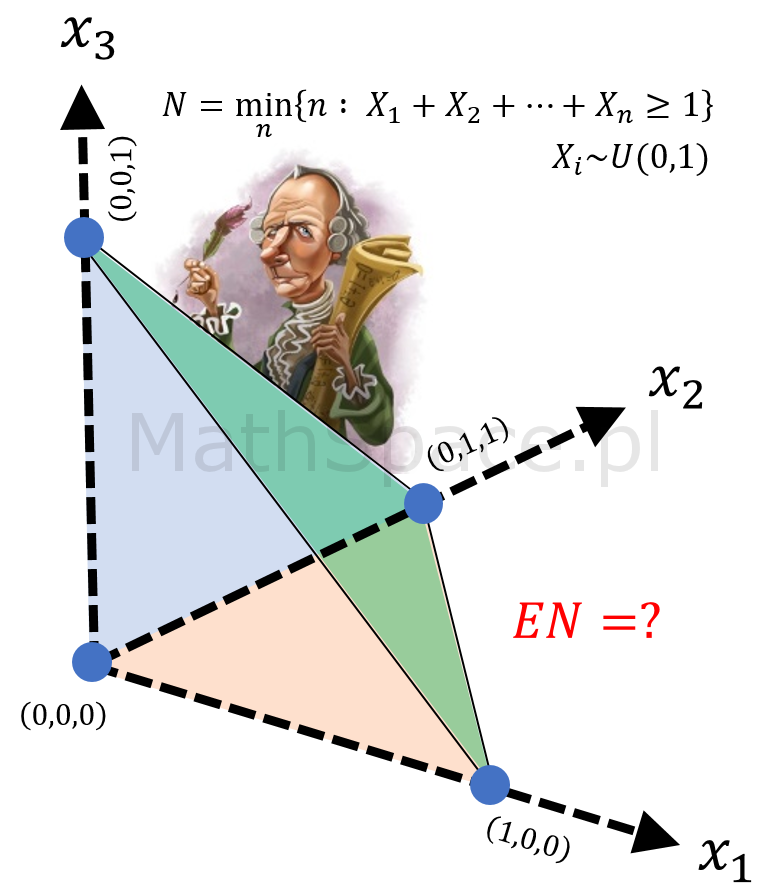
Pole powierzchni figur płaskich podobnych zmienia się z kwadratem skali podobieństwa – fakt nauczany już w szkole podstawowej. Dziś zadajemy pytanie „dlaczego” tak jest? O ile uzasadnienie dla najprostszych typów figur jest banalne (wynika bezpośrednio ze wzorów na pole), to w przypadku powierzchni ograniczonej dowolną krzywą (no może nie do końca dowolną) potrzeba już nieco więcej gimnastyki. Pokażę kilka podjeść, w tym osobno „pokryciowe”, osobno oparte na całce Riemanna, oraz osobno na bazie przekształcenia liniowego. Na koniec podam bardziej ogólne wnioski co do zmiany pola powierzchni względem znacznie szerszej niż podobieństwo klasy transformacji. Zapraszam 🙂

Czym jest podobieństwo?

Continue reading

by ·2 komentarze

Standaryzacja zmiennej losowej / Standaryzacja funkcji gęstości

Standaryzacja zmiennej losowej $X$ to proces jej „normalizacji”, którego wynikiem jest taka zmienna losowa $Z$, że

$$\text{E}Z=0$$

$$\text{Var}(Z)=1$$

Standaryzację łatwo wyobrazić sobie jako działanie, które obywa się w dwóch krokach:

  1. adekwatne „przesunięcie” zmiennej – tu chodzi o uzyskanie zerowej miary położenia, którą jest wartość oczekiwana (wartość średnia) zmiennej
  2. odpowiednia „zmiana skali wartości” zmiennej – w tym przypadku „poprawiamy” miarę rozproszenia, którą jest wariancja.

Standaryzacja Z: jeśli X jest taką zmienną losową, że

Continue reading

by ·0 Comments

Prelekcja wygłoszona w dniu 25.04.2017 podczas Konferencji Big Data – Bigger opportunities – zapraszam.

Omówione zagadnienia:

  • Analityka Predykcyjna
  • Model Predykcyjny
  • Confusion Matrix / Macierz błędu
  • Strategie doboru punktu odcięcia
  • Ocena jakości klasyfikacji
  • Krzywa zysku
  • Krzywa Lift
  • Krzywa ROC i wskaźnik Giniego
  • Krzywa Zysku vs ROC – równoważność?
  • Modele teoretycznie idealne

Odczarowujemy modele predykcyjne

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

I Am Here – RELEARN – Mariusz Gromada (2024)
I Am Here – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa

by ·2 komentarze

Agnostycyzm – bliska mi postawa.

Świetnie to wyjaśnia genialny fizyk – Leonard Susskind.

Inne posty w cyklu „Matematyka w obrazkach”.

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

I Am Here – RELEARN – Mariusz Gromada (2024)
I Am Here – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa

by ·0 Comments

Prelekcja wygłoszona w dniu 15.10.2015 podczas IV Konferencji Customer Intelligence – zapraszam.

Omówione zagadnienia:

  • Komponenty środowiska analitycznego
  • Cykl analityczny / Integracja
  • Architektura funkcjonalna środowiska
    – Obszar budowy / odkrywania wiedzy
    – Obszar wdrażania przygotowanych modeli predykcyjnych
    – Obszar repozytorium scoringowego
    – Obszar definicji oraz uruchomienia kampanii
    – Obszar monitoringu modeli predykcyjnych
    – Obszar raportowania kampanii
  • Pełny (360st) obraz klienta
  • Pomiar wartości – wpływ inkrementalny
  • Analityka – kilka ważnych rad

Skuteczna operacjonalizacja środowiska analitycznego

Pozdrowienia,

Mariusz Gromada

by ·0 Comments

Dziś głównym bohaterem cyklu „Matematyka w obrazkach” jest drapieżna funkcja odwrotna 🙂

Funkcja odwrotna

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

I Am Here – RELEARN – Mariusz Gromada (2024)
I Am Here – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)
Deep Under – RELEARN – Mariusz Gromada (2024)

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa

by ·2 komentarze

Inverse Transform Sampling to typowy sposób generowania liczb pseudolosowych z zadanego rozkładu, który opiera się na funkcji odwrotnej $F^{-1}$ do dystrybuanty $F$ tego rozkładu. Procedura jest banalna, wystarczy wylosować $Y\sim U(0,1)$ i zwrócić $F^{-1}(Y)$. Niestety nie zawsze łatwe jest wyznaczenie jawnej postaci dystrybuanty, tym bardziej dotyczy to funkcji do niej odwrotnej. Dla przykładu – powszechny rozkład normalny charakteryzuje się funkcją gęstości w postaci „elementarnej”, natomiast jego dystrybuanta (i funkcja do niej odwrotna) wymagają zastosowania funkcji specjalnych – w tym przypadku funkcji błędu Gaussa.

Kiedyś kolega (pozdrowienia Marcin!) pokazał mi nieskomplikowany sposób generacji liczb losowych z rozkładu opisanego histogramem. Zwyczajnie „kładziemy” (skalując) słupki histogramu na odcinek $(0,1)$, losujemy $X\sim U(0,1)$, weryfikujemy „do którego słupka wpadło X”, zwracamy „właśnie ten słupek”. Genialne w swojej prostocie, i działa. Histogram to dyskretna reprezentacja rozkładu, dlatego postanowiłem metodę uogólnić na klasę rozkładów ciągłych opisanych zadaną funkcją gęstości. Otrzymaną metodę nazwałem „MaCDRG-yver” 🙂

MaCDRG-yver - Monte Carlo Density based Random Generator

Continue reading

by ·0 Comments
1, 2, 3 - sympleks

Rozkład jednostajny na odcinku $(0,1)$, chyba najprostszy z możliwych rozkładów ciągłych, z pozoru niezbyt interesujący, a jednak 🙂 Dziś ciekawostka wiążąca rozkład sumy rozkładów jednostajnych z liczbą Eulera e.

Uniform Sum Distribution

Rozkład jednostajny ciągły na odcinku (a,b)

Rozkład jednostajny ciągły na odcinku $(a,b)$ jest opisany poniższą funkcją gęstości.

$$f(x)=\begin{cases}\frac{1}{b-a}&&\text{dla }a\leq x\leq b\\0&&\text{w p.p.}\end{cases}$$

Pisząc $X\sim U(a,b)$ oznaczamy, że zmienna losowa $X$ ma rozkład jednostajny ciągły na odcinku $(a,b)$. Jest to rozkład ciągły, zatem przyjęcie wartości $0$ lub $\frac{1}{b-a}$ w punktach $x=a$ i $x=b$ jest umowne i nie ma zwykle wpływu na własności i rozważania.

Continue reading