Wskaźnik Giniego, który opisałem w części #7 poświęconej krzywej ROC, jest jednym z najważniejszych narzędzi wykorzystywanych w procesie oceny jakości klasyfikacji. Choć krzywa ROC jest ważna i bardzo przydatna, to z mojego doświadczenia wynika, że większość analityków woli wykreślać krzywą Captured Response. Sądzę, że wszyscy intuicyjnie czujemy, że „Gini z ROC” i „Gini z Captured Response” to to samo 🙂 Ale dlaczego tak jest? 🙂 Dziś odpowiem na to pytanie, jednocześnie wzbogacając serię „Tips & Tricks na krzywych”!

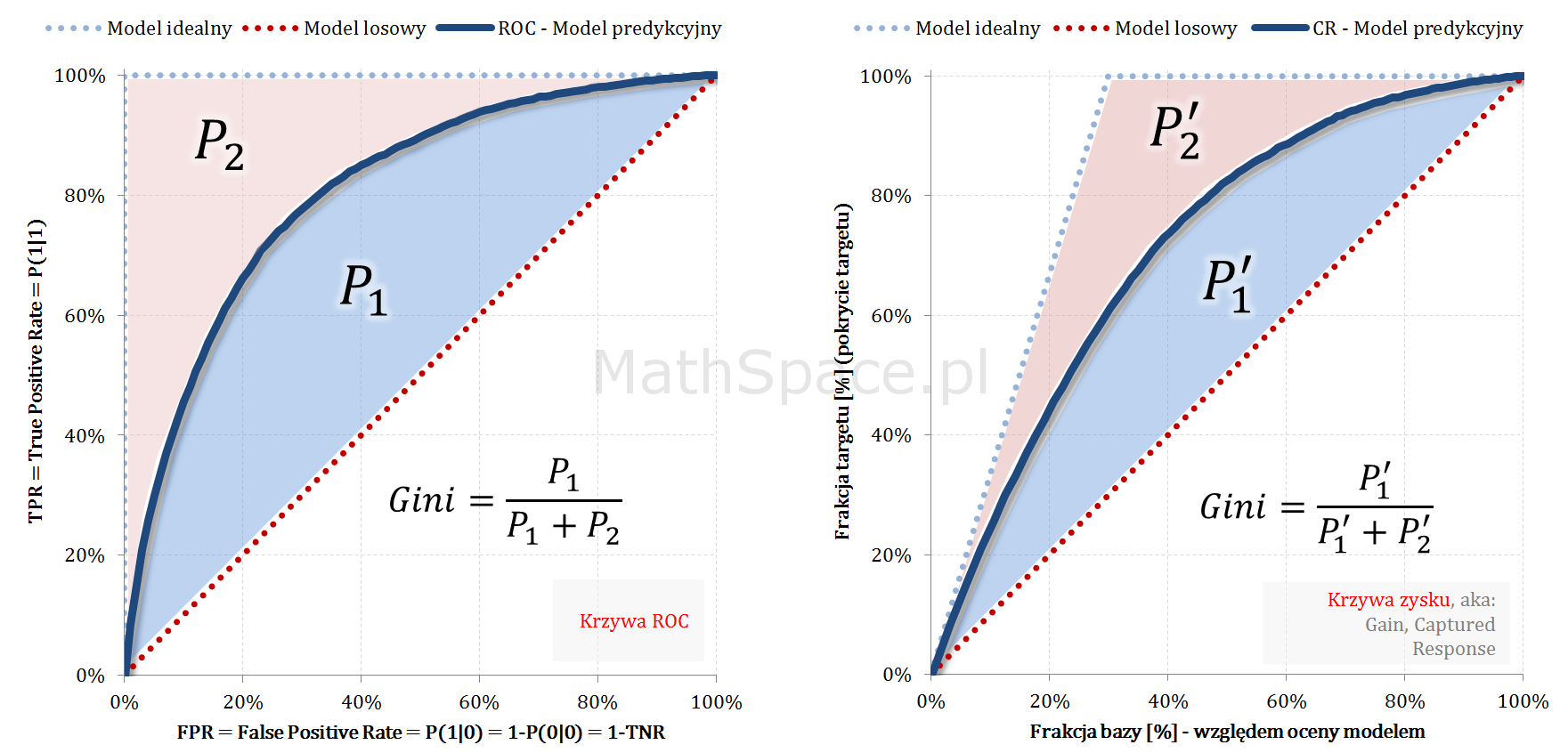
$$Gini=\frac{P_1}{P_1+P_2}=\frac{P_1^\prime}{P_1^\prime+P_2^\prime}$$

Krzywa Captured Response jako przekształcenie liniowe krzywej ROC

W części #8 wykazałem, że krzywą ROC i krzywą Captured Response łączy poniższa formuła.

$$X_{cr}=\Big(1-apriori\Big)\times X_{roc}+apriori\times Y_{roc}$$

$$Y_{cr}=Y_{roc}$$

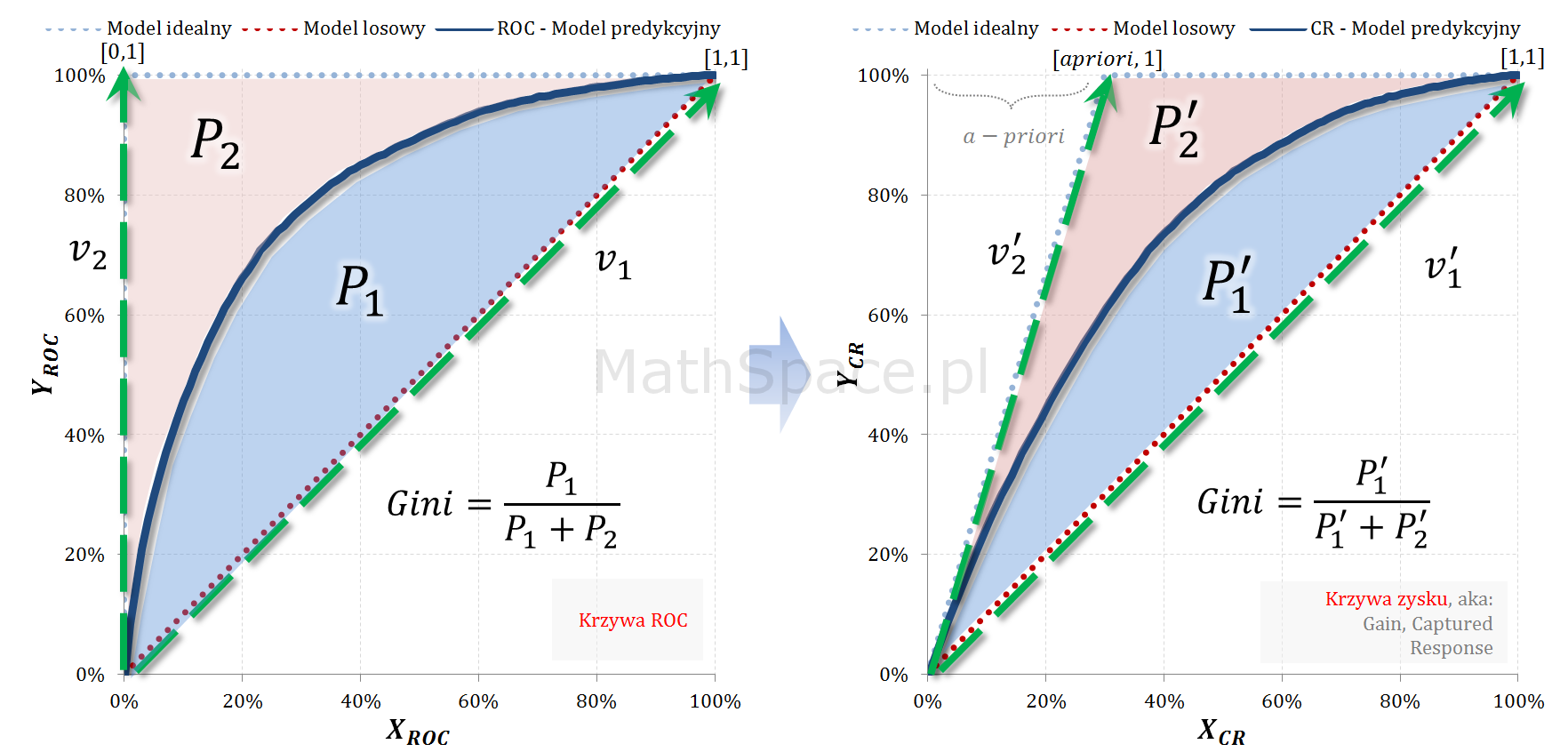
Powyższy wzór można zapisać na bazie przekształcenia liniowego

$$\begin{bmatrix}1-apriori & apriori\\0 & 1\end{bmatrix}\times\begin{bmatrix}X_{ROC}\\Y_{ROC}\end{bmatrix}=\begin{bmatrix}X_{CR}\\Y_{CR}\end{bmatrix}$$

 opisanego macierzą przekształcenia liniowego

$$A=\begin{bmatrix}1-apriori & apriori\\0 & 1\end{bmatrix}$$

Po szczegóły odsyłam do części #8 „Captured Response = ROC x apriori”.

Wyznacznik macierzy przekształcenia liniowego i współczynnik zmiany pola powierzchni

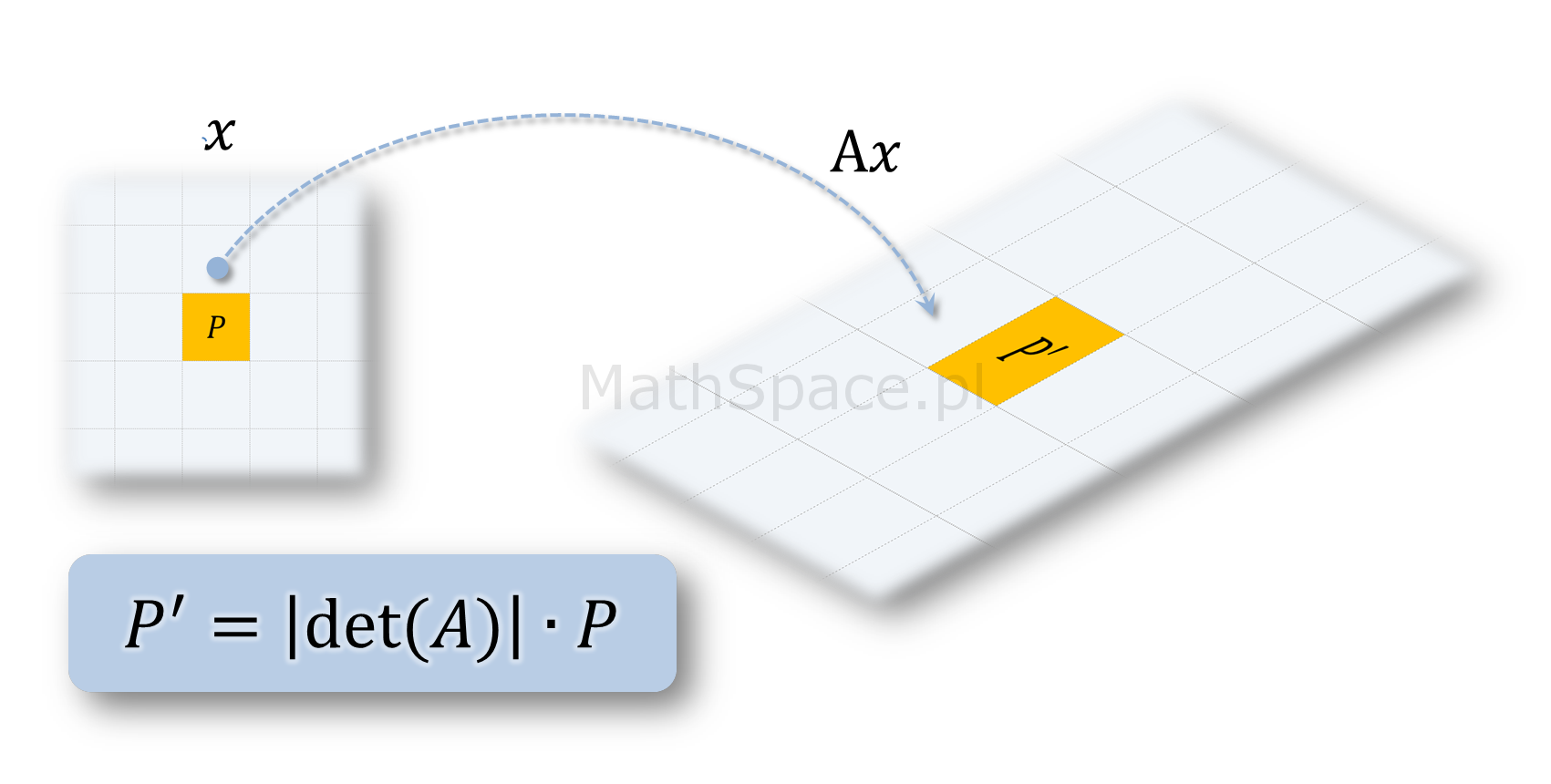
Jeśli analizujemy przekształcenie liniowe

$$Ax$$

gdzie $A$ jest macierzą przekształcenia liniowego, a $x$ wektorem, to wyznacznik

$$\text{det}(A)$$

jest współczynnikiem o jaki zmienia się pole powierzchni / objętość / miara figury / obiektu transformowanego poprzez przekształcenie liniowe $Ax$. Polecam poniższy film.

Wyznacznik macierzy przekształcenia liniowego krzywej ROC w krzywą Captured Response

$$\text{det}(A)=\text{det}\begin{bmatrix}1-apriori & apriori\\0 & 1\end{bmatrix}=1-apriori$$

Z powyższego wynika, że pole powierzchni pomiędzy przestrzenią, w której „osadzona” jest krzywa ROC, a przestrzenią „zawierającą” krzywą Captured Response, powinno się skalować poprzez współczynniki $1-apriori$. Sprawdźmy 🙂

$$P_1+P_2=\frac{1}{2}$$

Wykorzystując wzór na pole trójkąta wyznaczamy

$$P_1^\prime+P_2^\prime=\frac{1}{2}(1-apriori)$$

Zgadza się 🙂 I ostatecznie

$$\frac{P_1^\prime}{P_1^\prime+P_2^\prime}=\frac{P_1(1-apriori)}{(P_1+P2)(1-apriori)}=\frac{P_1}{P_1+P_2}$$

czyli

$$Gini=\frac{P_1}{P_1+P_2}=\frac{P_1^\prime}{P_1^\prime+P_2^\prime}$$

Jako ciekawostka – podobnie można policzyć AUROC z Captured Response:

$$AUROC=P_1+\frac{1}{2}=\frac{P_1^\prime}{1-apriori}+\frac{1}{2}$$

Pozdrowienia,

Mariusz Gromada

Poza Liczbami: Inne Twórcze Przestrzenie

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury

Matematyka i muzyka są ściśle powiązane przez rytm, harmonię i struktury, które wykorzystują matematyczne wzory i proporcje do tworzenia estetycznych i emocjonalnych doznań. Z nieśmiałą ekscytacją przedstawiam moją pierwszą poważniejszą kompozycję, w której starałem się uchwycić te połączenia.

Scalar – zaawansowana aplikacja mobilna z silnikiem matematycznym mojego autorstwa